前回の演習では、ネットワークに隠れ層を追加するだけでは非線形性を表現できないことを学びました。線形演算に対して実行される線形演算は、依然として線形です。
値間の非線形関係を学習するようにニューラル ネットワークを構成するにはどうすればよいですか?非線形数学演算をモデルに挿入する方法が必要です。
少し違和感があるかもしれませんが、これはコースの序盤に、線形モデルの出力に非線形算術演算を実際に適用したためです。ロジスティック回帰 モジュールでは、モデルの出力をシグモイド関数に渡すことで、0 ~ 1 の連続値(確率を表す)を出力するように線形回帰モデルを調整しました。
ニューラル ネットワークにも同じ原理を適用できます。先ほど演習 2 のモデルに戻りましょう。今回は、各ノードの値を出力する前に、まずシグモイド関数を適用します。
再生ボタンの右側にある >| ボタンをクリックして、各ノードの計算をステップ実行してみてください。グラフの下にある [計算] パネルで、各ノード値の計算に使用された数学演算を確認します。各ノードの出力は、前のレイヤのノードの線形結合のシグモイド変換になり、出力値はすべて 0 と 1 の間で縮小されます。
ここで、シグモイドはニューラル ネットワークの活性化関数として機能します。これは、値がニューラル ネットワークの次のレイヤの計算に入力として渡される前に、ニューロンの出力値を非線形に変換します。
活性化関数を追加したので、層を追加するとより大きな影響が得られます。非線形性を積み重ねることで、入力と予測出力間の非常に複雑な関係をモデル化できます。簡単に言うと、各レイヤは、元の入力に対してより複雑で上位レベルの関数を効果的に学習します。この仕組みについて理解を深めたい場合は、Chris Olah の優れたブログ投稿をご覧ください。
一般的な活性化関数
活性化関数としてよく使用される 3 つの数学関数は、シグモイド、tanh、ReLU です。
上記のシグモイド関数は、入力 $x$ に対して次の変換を行い、0 ~ 1 の範囲の出力値を生成します。
\[F(x)=\frac{1} {1+e^{-x}}\]
この関数をプロットすると、次のようになります。
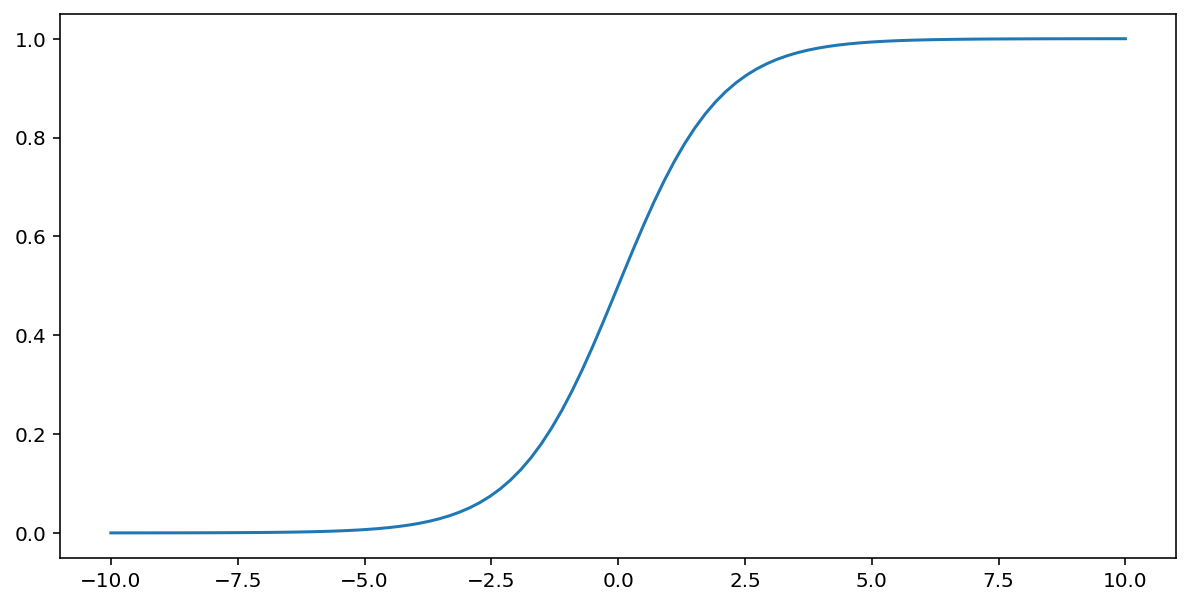
tanh(「双曲線正接」の略)関数は、入力 $x$ を変換して –1 ~ 1 の間の出力値を生成します。
\[F(x)=tanh(x)\]
この関数のグラフは次のとおりです。
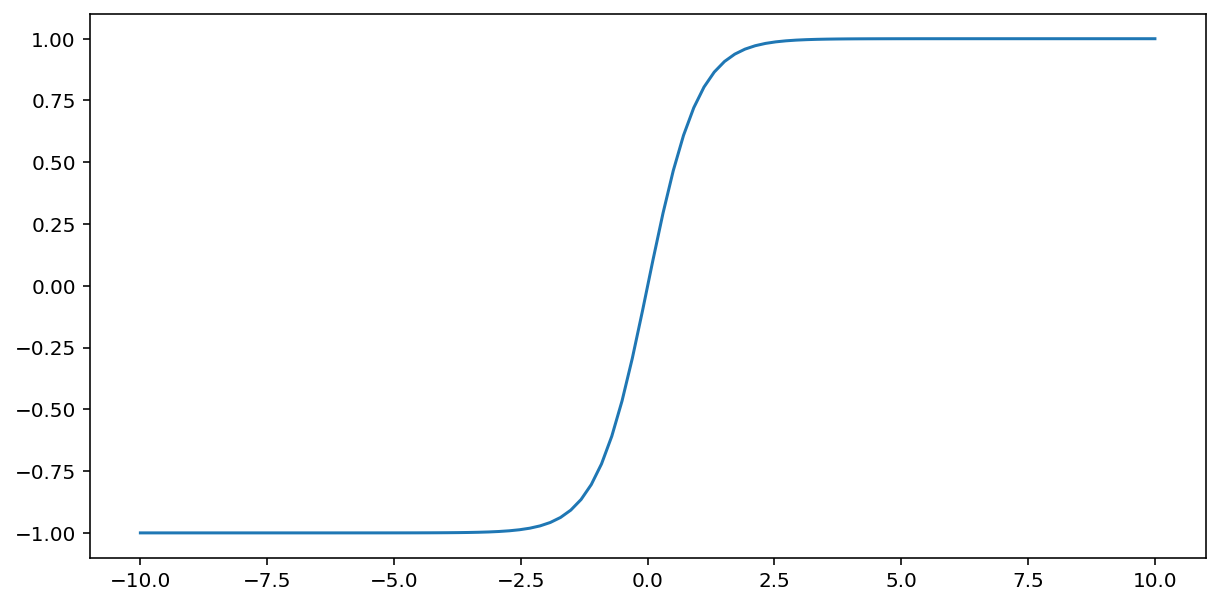
正規化線形ユニット活性化関数(略して ReLU)は、次のアルゴリズムを使用して出力を変換します。
- 入力値 $x$ が 0 未満の場合は 0 を返します。
- 入力値 $x$ が 0 以上の場合は、入力値を返します。
ReLU は、max() 関数を使用して数学的に表すことができます。
この関数のグラフを次に示します。
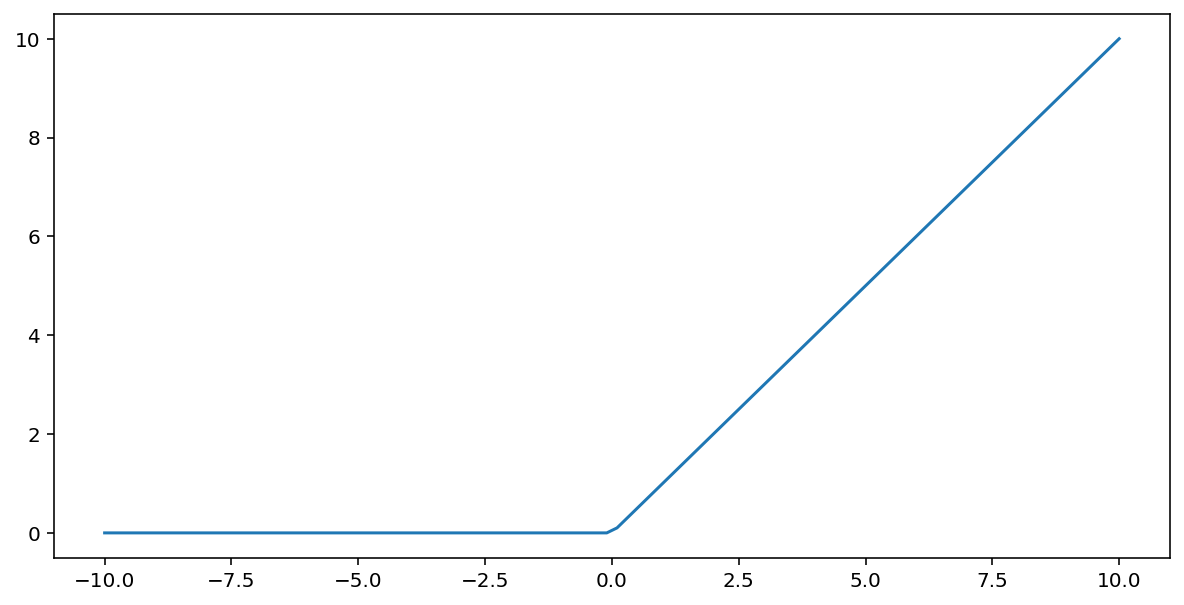
多くの場合、ReLU は、ニューラル ネットワークのトレーニング中に勾配消失の問題の影響を受けにくいため、シグモイドや tanh などの滑らかな関数よりも活性化関数として適しています。また、ReLU はこれらの関数よりも計算がはるかに簡単です。
その他の活性化関数
実際には、任意の数学関数を活性化関数として使用できます。 \(\sigma\) が活性化関数を表すとします。ネットワーク内のノードの値は次の式で示されます。
Keras は、多くの活性化関数をすぐに使用できます。ただし、最初は ReLU を使用することをおすすめします。
概要
次の動画では、ニューラル ネットワークの構築方法についてこれまで学んだことをすべてまとめています。
これで、モデルがニューラル ネットワークを指すときに通常意味するすべての標準コンポーネントがモデルに揃いました。
- ニューロンに似た一連のノードが層状に編成されています。
- 各ニューラル ネットワーク レイヤとその下のレイヤ間の接続を表す重みのセット。下位レイヤは、別のニューラル ネットワーク レイヤまたは他の種類のレイヤにすることができます。
- ノードごとに 1 つずつ、一連のバイアス。
- レイヤ内の各ノードの出力を変換する活性化関数。層によって活性化関数が異なる場合があります。
注意: ニューラル ネットワークは、必ずしも特徴クロスよりも優れているわけではありませんが、多くのケースで効果を発揮する柔軟な代替手段です。
