W poprzednim ćwiczeniu widzieliśmy, że samo dodanie ukrytych warstw do naszej sieci nie wystarcza do przedstawienia nieliniowości. Operacje liniowe wykonywane na operacjach liniowych są nadal liniowe.
Jak skonfigurować sieć neuronową, aby uczyła się nieliniowych relacji między wartościami? Potrzebujemy sposobu na wstawianie do modelu nieliniowych operacji matematycznych.
Jeśli to brzmi znajomo, to dlatego, że wcześniej w tym kursie stosowaliśmy operacje matematyczne nieliniowe do danych wyjściowych modelu liniowego. W module Regresja logistyczna dostosowaliśmy model regresji liniowej, aby zwracał wartość ciągłą z zakresu od 0 do 1 (reprezentującą prawdopodobieństwo), podając wynik modelu przez funkcję sigmoidalną.
Tę samą zasadę możemy zastosować do sieci neuronowej. Wróćmy do naszego modelu z Ćwiczenia 2 wcześniej, ale tym razem, zanim wartość każdego węzła wyświetlimy, użyjemy funkcji sigmoidalnej:
Aby sprawdzić obliczenia każdego węzła, kliknij przycisk >| (po prawej stronie przycisku odtwarzania). W panelu Obliczenia pod wykresem możesz przejrzeć operacje matematyczne wykonane, aby obliczyć każdą wartość węzła. Pamiętaj, że wyjście każdego węzła jest teraz transformacją sigmoidalną liniowej kombinacji węzłów z poprzedniej warstwy, a wartości wyjściowe są ściśnięte w zakresie od 0 do 1.
W tym przypadku funkcja sigmoidalna pełni rolę funkcji aktywacyjnej sieci neuronowej, nieliniowej transformacji wartości wyjściowej neurona, która jest przekazywana jako dane wejściowe do obliczeń kolejnej warstwy sieci neuronowej.
Dodaliśmy funkcję aktywacji, dzięki której dodanie warstw ma większy wpływ. Nakładanie nieliniowości na nieliniowości pozwala nam modelować bardzo skomplikowane relacje między danymi wejściowymi a prognozowanymi wynikami. Krótko mówiąc, każda warstwa skutecznie uczy się bardziej złożonej funkcji wyższego poziomu na podstawie nieprzetworzonych danych wejściowych. Jeśli chcesz dowiedzieć się więcej o tym, jak to działa, przeczytaj wybitny post Chrisa Olaha na blogu.
Typowe funkcje aktywacyjne
Trzy funkcje matematyczne, które są często używane jako funkcje aktywacyjne, to sigmoidalna, tanh i ReLU.
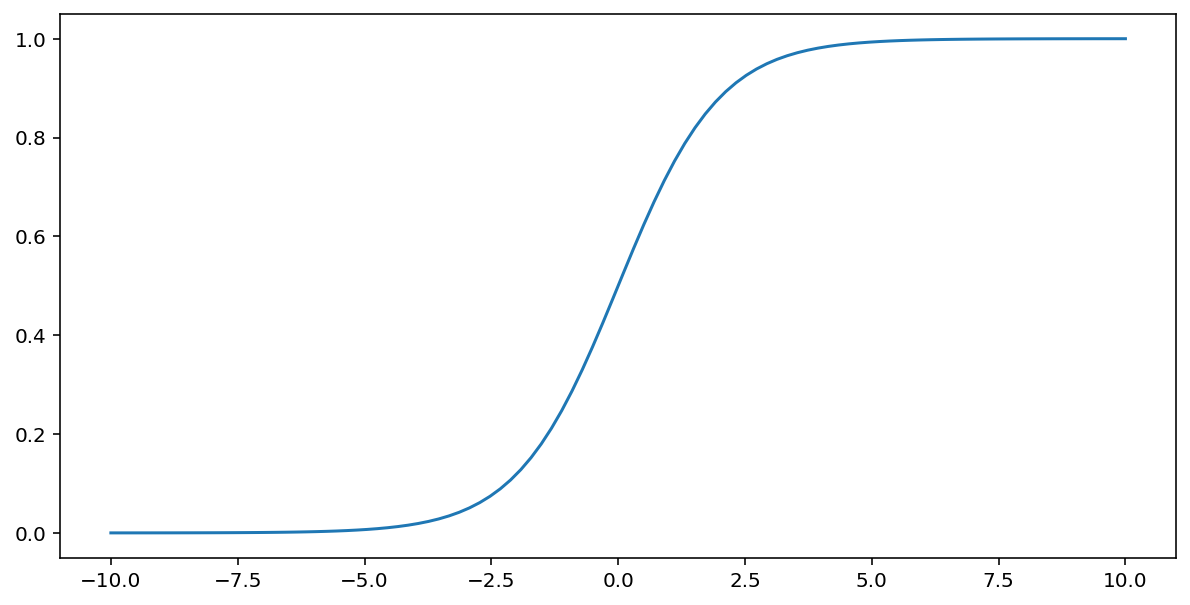
Funkcja sigmoidalna (omówiona powyżej) wykonuje tę transformację na wartości wejściowej $x$, zwracając wartość wyjściową z zakresu od 0 do 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Oto schemat tej funkcji:
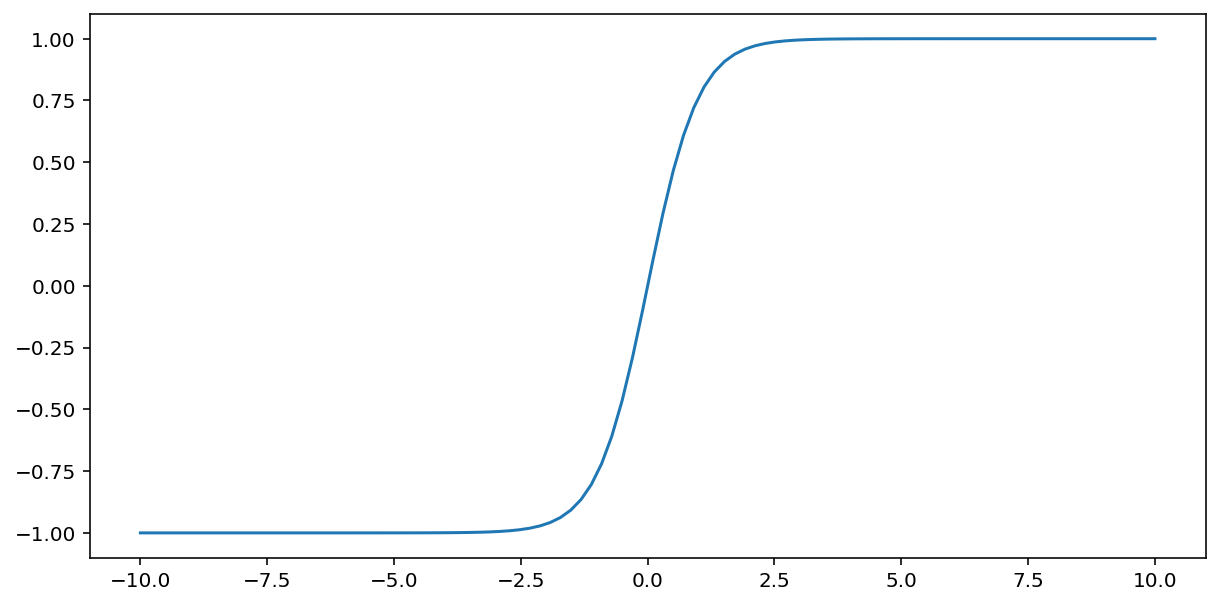
Funkcja tanh (skrót od „tangencja hiperboliczna”) przekształca wartość wejściową $x$ w wartość wyjściową z zakresu –1 i 1:
\[F(x)=tanh(x)\]
Oto wykres tej funkcji:
Funkcja aktywacji rectified linear unit (lub w skrócie ReLU) przekształca dane wyjściowe za pomocą tego algorytmu:
- Jeśli podana wartość $x$ jest mniejsza niż 0, zwraca 0.
- Jeśli podana wartość $x$ jest większa lub równa 0, zwraca podawaną wartość.
ReLU można przedstawić matematycznie przy użyciu funkcji max():
Oto wykres tej funkcji:
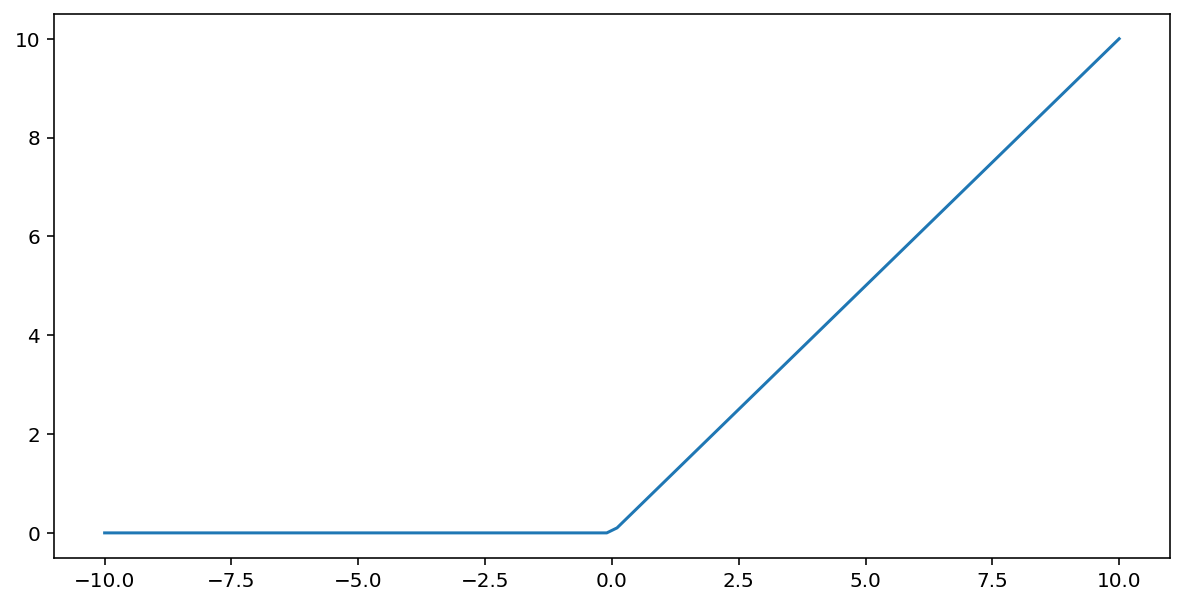
Funkcja ReLU często sprawdza się nieco lepiej jako funkcja aktywacji niż gładka funkcja, np. sigmoidalna lub tanh, ponieważ jest mniej podatna na problem zanikania gradientu podczas trenowania sieci neuronowej. Funkcja ReLU jest też znacznie łatwiejsza do obliczenia niż te funkcje.
Inne funkcje aktywacji
W praktyce dowolna funkcja matematyczna może pełnić funkcję funkcji aktywacji. Załóżmy, że \(\sigma\) reprezentuje naszą funkcję aktywacji. Wartość węzła w sieci jest określana za pomocą tej formuły:
Keras zapewnia obsługę wielu funkcji aktywacji. Mimo to zalecamy rozpoczęcie od ReLU.
Podsumowanie
W tym filmie znajdziesz podsumowanie wszystkich informacji, które do tej pory poznaliśmy na temat budowy sieci neuronowych:
Nasz model zawiera wszystkie standardowe komponenty, które zwykle kojarzą się z siecią neuronową:
- Zbiór węzłów analogicznych do neuronów i ułożonych w warstwy.
- Zestaw wag reprezentujących połączenia między poszczególnymi warstwami sieci neuronowej i położoną niżej warstwą. Warstwa poniżej może być kolejną warstwą sieci neuronowej lub inną warstwą.
- Zbiór odchylenia, po jednym dla każdego węzła.
- Funkcja aktywacji, która przekształca wyjście każdego węzła w warstwie. Różne warstwy mogą mieć różne funkcje aktywacji.
Uwaga: sieci neuronowe nie zawsze są lepsze od krzyżowania cech, ale stanowią elastyczną alternatywę, która sprawdza się w wielu przypadkach.
