Önceki alıştırmada, ağımıza gizli katmanlar eklemenin, doğrusal olmayanlıkları temsil etmek için yeterli olmadığını görmüştünüz. Doğrusal işlemler üzerinde gerçekleştirilen doğrusal işlemler yine doğrusaldır.
Bir nöral ağı, değerler arasındaki doğrusal olmayan ilişkileri öğrenecek şekilde nasıl yapılandırabilirsiniz? Bir modele doğrusal olmayan matematiksel işlemleri eklemenin bir yoluna ihtiyacımız var.
Bu size tanıdık geliyorsa bunun nedeni, kursun önceki bölümlerinde doğrusal bir modelin çıktısına doğrusal olmayan matematiksel işlemler uygulamış olmamızdır. Mantıksal Regresyon modülünde, doğrusal regresyon modelini, modelin çıktısını sigmoid işlevi üzerinden geçirerek 0 ile 1 arasında kesintisiz bir değer (bir olasılığı temsil eder) döndürecek şekilde uyarladık.
Aynı ilkeyi nöral ağımıza uygulayabiliriz. Daha önceki Alıştırma 2'deki modelimize tekrar bakalım. Bu kez her düğümün değerini çıkarmadan önce sigmoid işlevini uygulayacağız:
>| düğmesini (oynat düğmesinin sağındaki) tıklayarak her bir düğümün hesaplamalarını adım adım incelemeyi deneyin. Grafiğin altındaki Hesaplamalar panelinde her düğüm değerini hesaplamak için gerçekleştirilen matematik işlemlerini inceleyin. Her bir düğümün çıktısının artık önceki katmandaki düğümlerin doğrusal kombinasyonunun sigmoid dönüşümü olduğunu ve çıkış değerlerinin hepsinin 0 ile 1 arasında sıkıştırıldığını unutmayın.
Burada sigmoid, sinir ağı için bir etkinleştirme işlevi olarak işlev görür. Bu işlev, sinir ağının bir sonraki katmanının hesaplamalarına giriş olarak aktarılmadan önce bir nöronun çıkış değerinin doğrusal olmayan bir dönüşümüdür.
Artık bir etkinleştirme işlevi eklediğimize göre, katman eklemenin daha fazla etkisi var. Doğrusal olmayanlar üzerinde doğrusal olmayanları yığmak, girişler ile tahmin edilen çıkışlar arasındaki çok karmaşık ilişkileri modellememize olanak tanır. Özetlemek gerekirse her katman, ham girişler üzerinden daha karmaşık ve üst düzey bir işlevi etkili bir şekilde öğrenir. Bunun işleyiş şekli hakkında daha fazla bilgi edinmek istiyorsanız Chris Olah'ın mükemmel blog yayınını inceleyin.
Sık kullanılan etkinleştirme işlevleri
Genellikle aktivasyon işlevi olarak kullanılan üç matematiksel işlev sigmoid, tanh ve ReLU'dur.
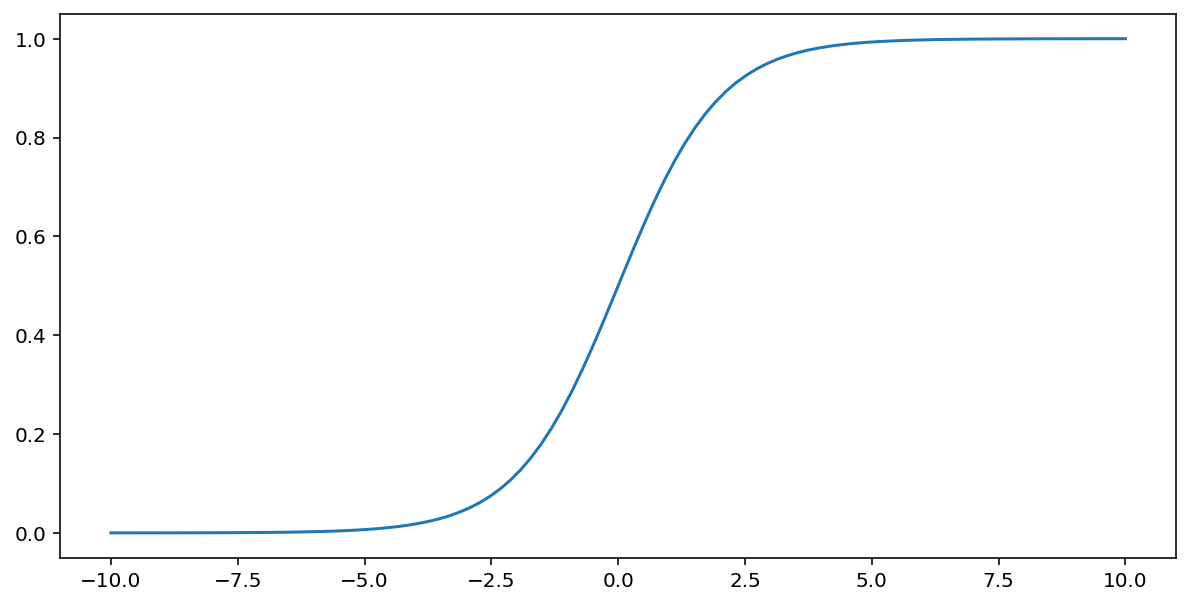
Sigmoid işlevi (yukarıda açıklanmıştır), $x$ girişinde aşağıdaki dönüşümü gerçekleştirir ve 0 ile 1 arasında bir çıkış değeri üretir:
\[F(x)=\frac{1} {1+e^{-x}}\]
Bu işlevin grafiği aşağıda verilmiştir:
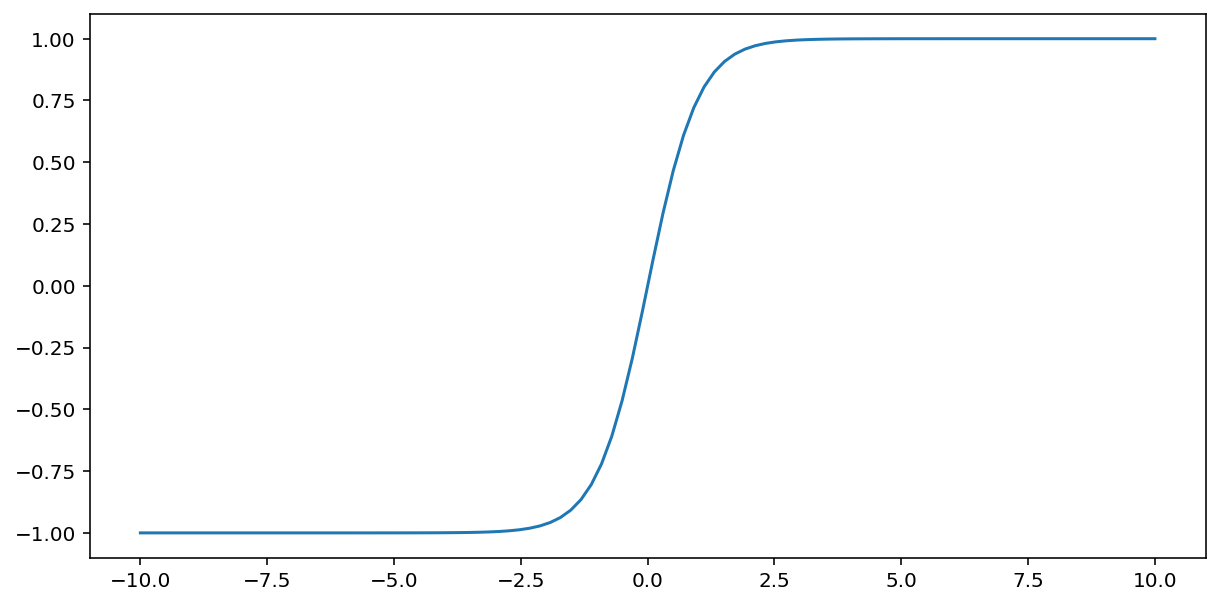
tanh ("hiperbolik tanjant"ın kısaltması) işlevi, giriş $x$ değerini dönüştürerek -1 ile 1 arasında bir çıkış değeri oluşturur:
\[F(x)=tanh(x)\]
Bu fonksiyonun grafiğini aşağıda görebilirsiniz:
Düzeltilmiş doğrusal birim aktivasyon işlevi (veya kısaca ReLU), aşağıdaki algoritmayı kullanarak çıkışı dönüştürür:
- Giriş değeri $x$ 0'dan azsa 0 döndürülür.
- Giriş değeri $x$ 0'dan büyük veya 0'a eşitse giriş değerini döndürür.
ReLU, max() işlevi kullanılarak matematiksel olarak temsil edilebilir:
Bu fonksiyonun grafiğini aşağıda görebilirsiniz:
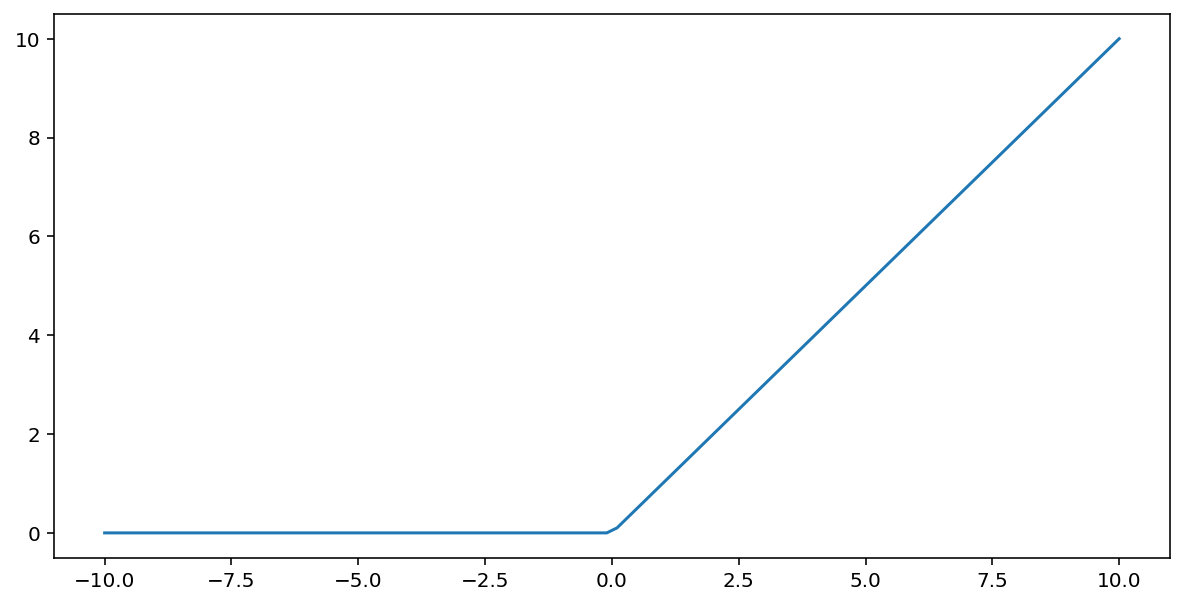
ReLU, sinir ağı eğitimi sırasında gradyan kaybolma sorununa daha az duyarlı olduğundan, aktivasyon işlevi olarak genellikle sigmoid veya tanh gibi düz bir işlevden biraz daha iyi çalışır. ReLU'nun hesaplanmasının bu işlevlere kıyasla çok daha kolay olması da bir avantajdır.
Diğer etkinleştirme işlevleri
Pratikte, herhangi bir matematiksel işlev aktivasyon işlevi olarak kullanılabilir. \(\sigma\) işlevinin etkinleştirme işlevimizi temsil ettiğini varsayalım. Ağdaki bir düğümün değeri aşağıdaki formülle verilir:
Keras, birçok etkinleştirme işlevi için kullanıma hazır destek sağlar. Yine de ReLU ile başlamanızı öneririz.
Özet
Aşağıdaki videoda, nöral ağların nasıl oluşturulduğu hakkında şimdiye kadar öğrendiğiniz her şey özetlenmiştir:
Artık modelimiz, insanların bir nöral ağa atıfta bulunduklarında genellikle ne ifade ettikleriyle ilgili tüm standart bileşenlere sahip:
- Katmanlar halinde düzenlenmiş, nöronlara benzeyen bir düğüm kümesi.
- Her nöral ağ katmanı ile altındaki katman arasındaki bağlantıları temsil eden bir ağırlık grubu. Altındaki katman başka bir nöral ağ katmanı veya farklı türde bir katman olabilir.
- Her düğüm için bir tane olmak üzere bir önyargı grubu.
- Bir katmandaki her düğümün çıkışını dönüştüren bir etkinleştirme işlevi. Farklı katmanların farklı etkinleştirme işlevleri olabilir.
Bir uyarı: Nöral ağlar her zaman özellik çaprazlamalarından daha iyi değildir ancak birçok durumda iyi çalışan esnek bir alternatif sunarlar.
