Trong bài tập trước, bạn đã thấy rằng việc chỉ thêm các lớp ẩn vào mạng của chúng ta là chưa đủ để biểu thị các hàm phi tuyến tính. Các phép toán tuyến tính được thực hiện trên các phép toán tuyến tính vẫn là tuyến tính.
Làm cách nào để bạn có thể định cấu hình mạng nơron để tìm hiểu các mối quan hệ phi tuyến tính giữa các giá trị? Chúng ta cần một số cách để chèn các phép toán không tuyến tính vào mô hình.
Nếu bạn thấy điều này có vẻ quen thuộc, thì đó là do chúng tôi đã thực sự áp dụng các phép toán phi tuyến tính cho kết quả của mô hình tuyến tính trước đó trong khoá học. Trong mô-đun Logistic Regression (Phương pháp hồi quy logistic), chúng tôi đã điều chỉnh mô hình hồi quy tuyến tính để xuất ra một giá trị liên tục từ 0 đến 1 (biểu thị xác suất) bằng cách truyền đầu ra của mô hình thông qua hàm sigmoid.
Chúng ta có thể áp dụng nguyên tắc tương tự cho mạng nơron. Hãy xem lại mô hình của chúng ta từ Bài tập 2 trước đó, nhưng lần này, trước khi xuất giá trị của mỗi nút, trước tiên chúng ta sẽ áp dụng hàm sigmoid:
Hãy thử thực hiện từng bước tính toán của mỗi nút bằng cách nhấp vào nút >| (ở bên phải nút phát). Xem lại các phép toán đã thực hiện để tính từng giá trị nút trong bảng điều khiển Tính toán bên dưới biểu đồ. Lưu ý rằng đầu ra của mỗi nút hiện là một phép biến đổi sigmoid của tổ hợp tuyến tính của các nút trong lớp trước và tất cả các giá trị đầu ra đều nằm trong khoảng từ 0 đến 1.
Ở đây, hàm sigmoid đóng vai trò là hàm kích hoạt cho mạng nơron, một phép biến đổi phi tuyến tính của giá trị đầu ra của một nơron trước khi giá trị này được truyền dưới dạng dữ liệu đầu vào cho các phép tính của lớp tiếp theo của mạng nơron.
Bây giờ chúng ta đã thêm hàm kích hoạt, việc thêm các lớp sẽ có nhiều tác động hơn. Việc xếp chồng phi tuyến tính trên các phi tuyến tính cho phép chúng ta lập mô hình các mối quan hệ rất phức tạp giữa các đầu vào và đầu ra dự đoán. Tóm lại, mỗi lớp đang học hiệu quả một hàm phức tạp hơn, cấp cao hơn so với dữ liệu đầu vào thô. Nếu bạn muốn tìm hiểu thêm về cách hoạt động của phương pháp này, hãy xem bài đăng tuyệt vời trên blog của Chris Olah.
Các hàm kích hoạt phổ biến
Ba hàm toán học thường được dùng làm hàm kích hoạt là sigmoid, tanh và ReLU.
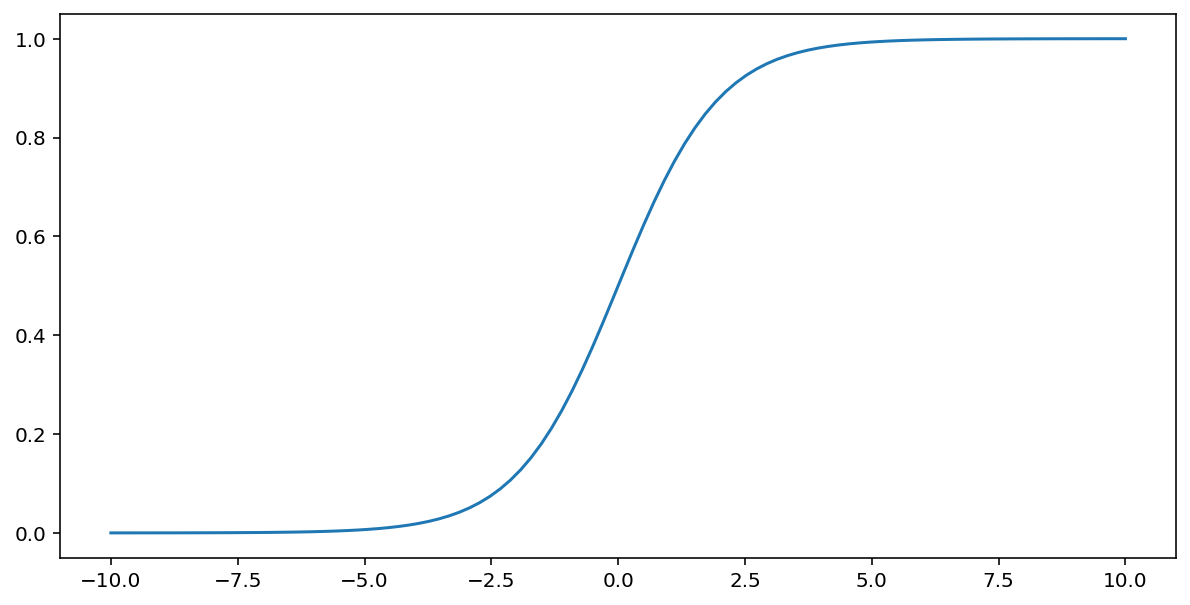
Hàm sigmoid (đã thảo luận ở trên) thực hiện phép biến đổi sau đây trên đầu vào $x$, tạo ra một giá trị đầu ra nằm trong khoảng từ 0 đến 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Dưới đây là đồ thị của hàm này:
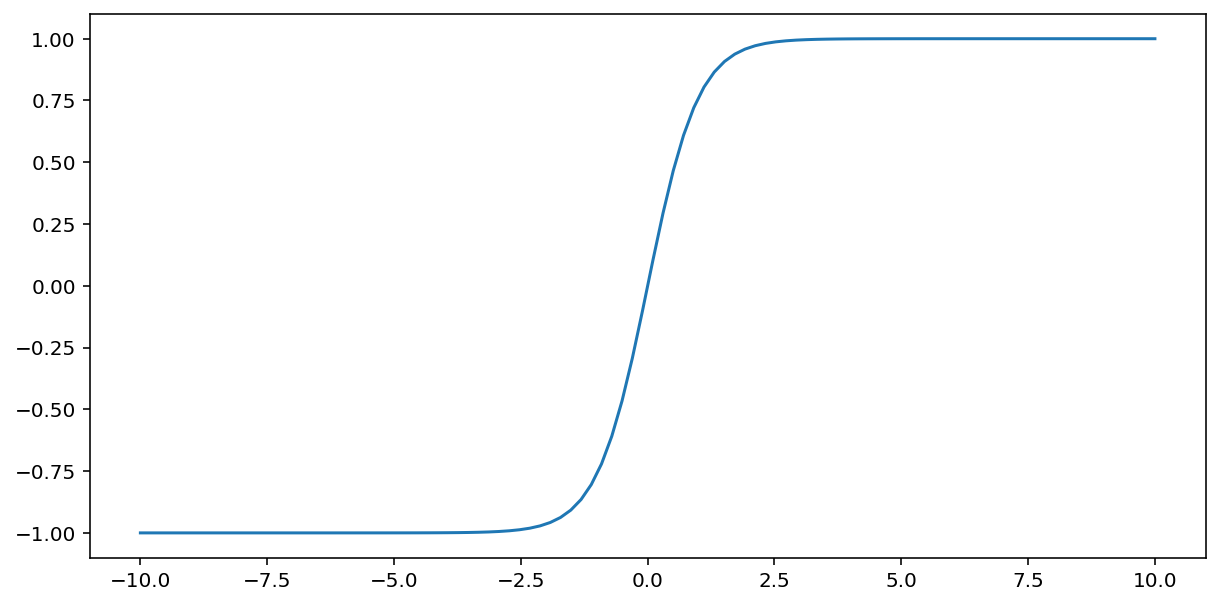
Hàm tanh (viết tắt của "hyperbolic tangent" – hàm tang hyperbol) biến đổi dữ liệu đầu vào $x$ để tạo ra một giá trị đầu ra nằm trong khoảng từ –1 đến 1:
\[F(x)=tanh(x)\]
Dưới đây là đồ thị của hàm này:
Hàm kích hoạt đơn vị tuyến tính chỉnh lưu (hay gọi tắt là ReLU) biến đổi đầu ra bằng thuật toán sau:
- Nếu giá trị đầu vào $x$ nhỏ hơn 0, hãy trả về 0.
- Nếu giá trị đầu vào $x$ lớn hơn hoặc bằng 0, hãy trả về giá trị đầu vào.
Bạn có thể biểu thị ReLU bằng toán học bằng cách sử dụng hàm max():
Dưới đây là đồ thị của hàm này:
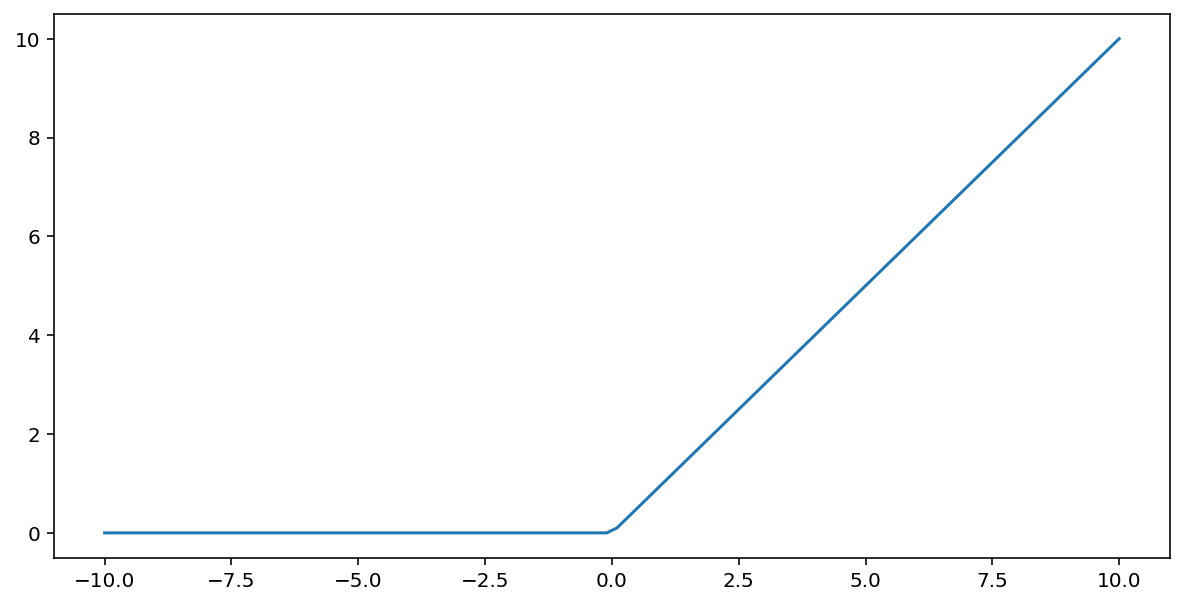
ReLU thường hoạt động tốt hơn một chút với vai trò kích hoạt so với một hàm trơn tru như sigmoid hoặc tanh, vì hàm này ít ảnh hưởng đến hơn với vấn đề về độ dốc biến mất trong quá trình huấn luyện mạng nơron. ReLU cũng dễ tính toán hơn đáng kể so với các hàm này.
Các hàm kích hoạt khác
Trong thực tế, bất kỳ hàm toán học nào cũng có thể đóng vai trò là hàm kích hoạt. Giả sử \(\sigma\) đại diện cho hàm kích hoạt của chúng ta. Giá trị của một nút trong mạng được xác định theo công thức sau:
Keras cung cấp tính năng hỗ trợ ngay lập tức cho nhiều hàm kích hoạt. Tuy nhiên, bạn vẫn nên bắt đầu với ReLU.
Tóm tắt
Video sau đây tóm tắt mọi kiến thức bạn đã học được cho đến nay về cách xây dựng mạng nơron:
Bây giờ, mô hình của chúng ta đã có tất cả các thành phần tiêu chuẩn mà mọi người thường đề cập đến khi nói đến mạng nơron:
- Một tập hợp các nút, tương tự như các nơron, được sắp xếp theo lớp.
- Một tập hợp các trọng số đại diện cho các kết nối giữa mỗi lớp mạng nơron và lớp bên dưới. Lớp bên dưới có thể là một lớp mạng nơron khác hoặc một số loại lớp khác.
- Một tập hợp các độ lệch, một độ lệch cho mỗi nút.
- Hàm kích hoạt biến đổi đầu ra của mỗi nút trong một lớp. Các lớp khác nhau có thể có các hàm kích hoạt khác nhau.
Lưu ý: mạng nơron không phải lúc nào cũng tốt hơn tính năng chéo, nhưng mạng nơron cung cấp một giải pháp thay thế linh hoạt và hoạt động hiệu quả trong nhiều trường hợp.
