이전 연습문제에서 네트워크에 숨겨진 레이어를 추가하는 것만으로는 비선형성을 나타내기에 충분하지 않다는 것을 확인했습니다. 선형 연산에 대해 실행되는 선형 연산은 여전히 선형입니다.
값 간의 비선형 관계를 학습하도록 신경망을 구성하려면 어떻게 해야 할까요? 비선형 수학 연산을 모델에 삽입하는 방법이 필요합니다.
이 내용이 다소 익숙하다면 앞서 과정의 초반에 선형 모델의 출력에 비선형 수학 연산을 적용했기 때문입니다. 로지스틱 회귀 모듈에서는 모델의 출력을 시그모이드 함수를 통해 전달하여 0~1의 연속 값 (확률을 나타냄)을 출력하도록 선형 회귀 모델을 조정했습니다.
신경망에도 동일한 원칙을 적용할 수 있습니다. 앞서 실습 2의 모델을 다시 살펴보겠습니다. 이번에는 각 노드의 값을 출력하기 전에 먼저 시그모이드 함수를 적용합니다.
재생 버튼 오른쪽에 있는 >| 버튼을 클릭하여 각 노드의 계산을 단계별로 수행해 보세요. 그래프 아래의 계산 패널에서 각 노드 값을 계산하기 위해 수행된 수학 연산을 검토합니다. 이제 각 노드의 출력은 이전 레이어에 있는 노드의 선형 조합에 대한 시그모이드 변환이며, 출력 값은 모두 0과 1 사이로 찌그러집니다.
여기서 시그모이드는 신경망의 활성화 함수, 즉 신경망의 다음 레이어 계산에 입력값으로 전달되기 전에 뉴런의 출력 값에 대한 비선형 변환으로 사용됩니다.
이제 활성화 함수를 추가했으므로 레이어를 추가하면 더 큰 효과를 얻을 수 있습니다. 비선형성을 비선형성에 쌓으면 입력과 예측된 출력 간의 매우 복잡한 관계를 모델링할 수 있습니다. 간단히 말해 각 레이어는 원시 입력에 대해 더 복잡하고 상위 수준의 함수를 효과적으로 학습합니다. 작동 방식에 대한 직관을 키우려면 크리스 올라의 훌륭한 블로그 게시물을 참고하세요.
일반적인 활성화 함수
활성화 함수로 일반적으로 사용되는 세 가지 수학 함수는 시그모이드, tanh, ReLU입니다.
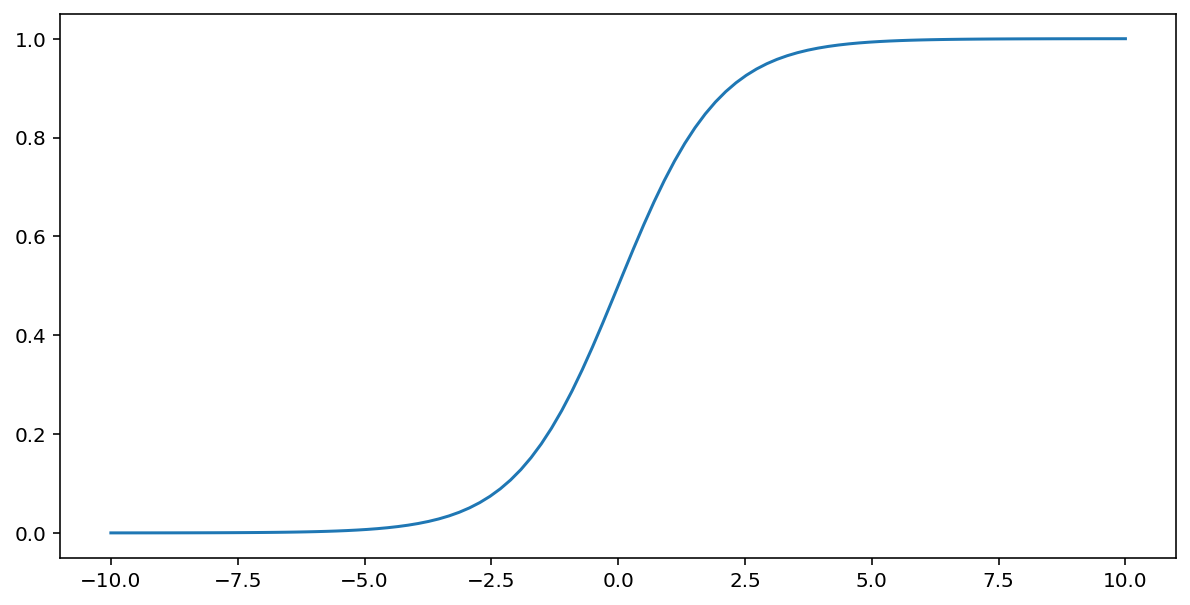
위에서 설명한 시그모이드 함수는 입력 $x$에 대해 다음 변환을 실행하여 0과 1 사이의 출력 값을 생성합니다.
\[F(x)=\frac{1} {1+e^{-x}}\]
다음은 이 함수의 그래프입니다.
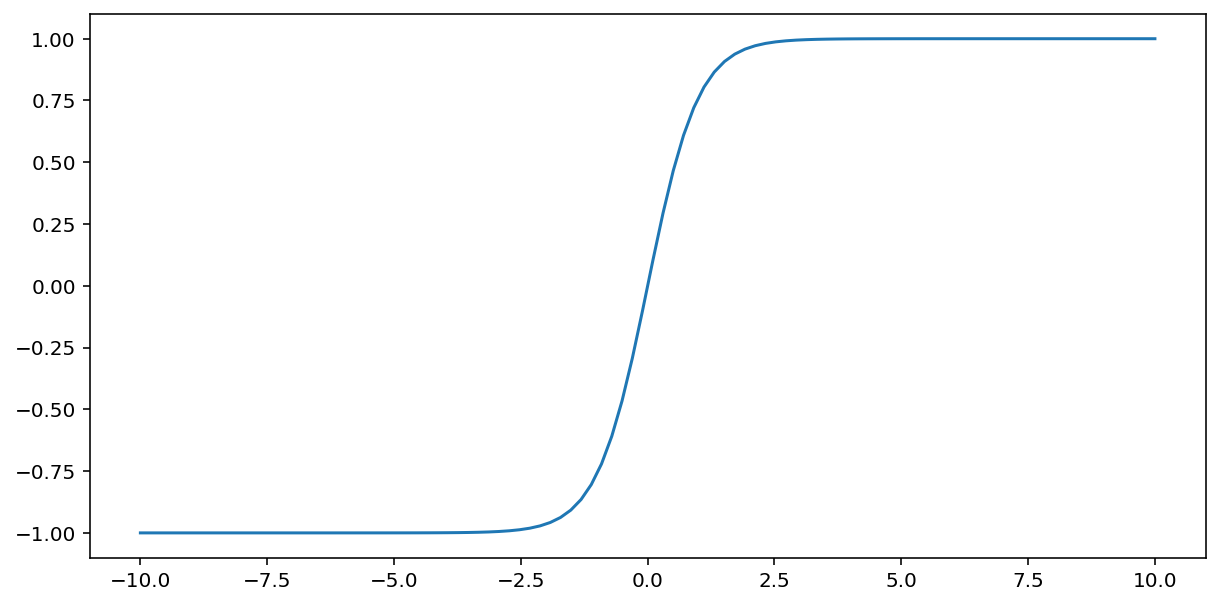
tanh('쌍곡선 탄젠트'의 줄임말) 함수는 입력 $x$ 를 변환하여 -1과 1 사이의 출력 값을 생성합니다.
\[F(x)=tanh(x)\]
이 함수의 도표는 다음과 같습니다.
정류 선형 유닛 활성화 함수 (줄여서 ReLU)는 다음 알고리즘을 사용하여 출력을 변환합니다.
- 입력 값 $x$ 가 0보다 작은 경우 0을 반환합니다.
- 입력 값 $x$ 가 0보다 크거나 같은 경우 입력 값을 반환합니다.
ReLU는 max() 함수를 사용하여 수학적으로 표현할 수 있습니다.
다음은 이 함수의 그래프입니다.
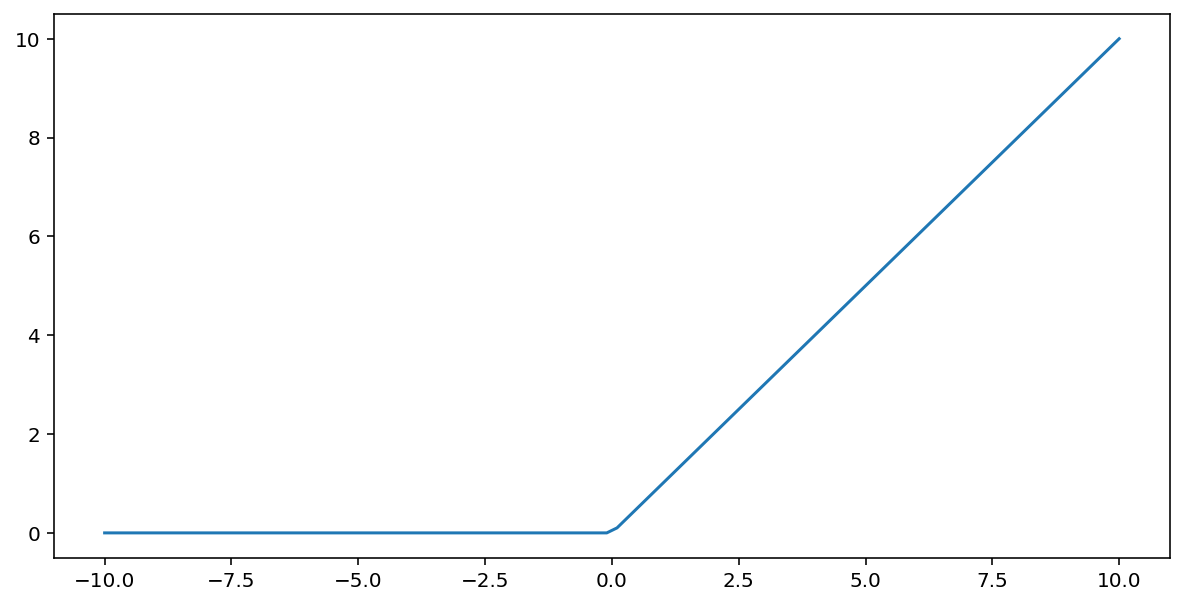
ReLU는 신경망 학습 중에 그라디언트 소실 문제에 영향을 덜 받으므로 시그모이드나 tanh와 같은 부드러운 함수보다 활성화 함수로 더 잘 작동하는 경우가 많습니다. ReLU는 이러한 함수보다 계산하기도 훨씬 쉽습니다.
기타 활성화 함수
실제로는 모든 수학 함수가 활성화 함수 역할을 할 수 있습니다. \(\sigma\) 가 활성화 함수를 나타낸다고 가정해 보겠습니다. 네트워크의 노드 값은 다음 공식으로 계산됩니다.
Keras는 여러 활성화 함수를 즉시 지원합니다. 하지만 ReLU로 시작하는 것이 좋습니다.
요약
다음 동영상에서는 신경망 구성 방법에 대해 지금까지 학습한 모든 내용을 요약합니다.
이제 모델에 사람들이 신경망을 언급할 때 일반적으로 의미하는 모든 표준 구성요소가 포함되었습니다.
- 뉴런과 유사한 노드 집합이 레이어에 구성되어 있습니다.
- 각 신경망 레이어와 하위 레이어와의 연결을 나타내는 가중치 집합이 있습니다. 하위 레이어는 또 다른 신경망 레이어이거나 유형이 다른 레이어일 수도 있습니다.
- 편향 집합이 각 노드에 하나씩 존재합니다.
- 레이어의 각 노드의 출력을 변환하는 활성화 함수입니다. 레이어마다 활성화 함수가 다를 수 있습니다.
주의: 신경망이 항상 특성 교차보다 나은 것은 아니지만 많은 경우에 효과적인 유연한 대안을 제공합니다.
