आपने पिछले एक्सरसाइज़ में देखा था कि नेटवर्क में सिर्फ़ छिपी हुई लेयर जोड़ने से, नॉन-लाइनियरिटी को दिखाने के लिए काफ़ी नहीं था. लीनियर ऑपरेशन पर किए गए लीनियर ऑपरेशन अब भी लीनियर होते हैं.
वैल्यू के बीच नॉन-लाइनियर संबंधों को जानने के लिए, न्यूरल नेटवर्क को कैसे कॉन्फ़िगर किया जा सकता है? हमें किसी मॉडल में नॉनलीनियर गणितीय संक्रियाएं डालने का कोई तरीका चाहिए.
अगर आपको यह कुछ हद तक जाना-पहचाना लग रहा है, तो इसकी वजह यह है कि हमने कोर्स के पहले हिस्से में, लीनियर मॉडल के आउटपुट पर नॉन-लीनियर मैथमैटिकल ऑपरेशन लागू किए हैं. लॉजिस्टिक रिग्रेशन मॉड्यूल में, हमने लीनियर रिग्रेशन मॉडल को 0 से 1 (संभावना दिखाने वाला) तक की लगातार वैल्यू दिखाने के लिए अडैप्ट किया है. इसके लिए, हमने मॉडल के आउटपुट को सिग्मॉइड फ़ंक्शन से पास किया है.
हम इस सिद्धांत को अपने न्यूरल नेटवर्क पर भी लागू कर सकते हैं. आइए, पहले एक्सरसाइज़ 2 के अपने मॉडल पर दोबारा जाते हैं, लेकिन इस बार, हर नोड की वैल्यू को आउटपुट करने से पहले, हम सबसे पहले सिग्मॉइड फ़ंक्शन को लागू करेंगे:
>| बटन (प्ले बटन की दाईं ओर) पर क्लिक करके, हर नोड की गणना की प्रक्रिया को देखें. ग्राफ़ के नीचे मौजूद कैलकुलेशन पैनल में, हर नोड की वैल्यू का हिसाब लगाने के लिए किए गए गणितीय ऑपरेशन देखें. ध्यान दें कि हर नोड का आउटपुट अब पिछली लेयर में मौजूद नोड के लीनियर कॉम्बिनेशन का सिग्मॉइड ट्रांसफ़ॉर्म है. साथ ही, आउटपुट की सभी वैल्यू 0 और 1 के बीच होती हैं.
इसमें सिगमॉइड, न्यूरल नेटवर्क के लिए ऐक्टिवेशन फ़ंक्शन के तौर पर काम करता है. न्यूरल नेटवर्क की अगली लेयर की कैलकुलेशन के लिए, वैल्यू को पास किए जाने से पहले यह न्यूरॉन की आउटपुट वैल्यू का एक नॉनलीनियर ट्रांसफ़ॉर्म होती है.
हमने ऐक्टिवेशन फ़ंक्शन जोड़ दिया है. इसलिए, लेयर जोड़ने से ज़्यादा असर पड़ता है. नॉन-लाइनियरिटी को एक-दूसरे पर स्टैक करने से, हमें इनपुट और अनुमानित आउटपुट के बीच के बहुत जटिल संबंधों को मॉडल करने में मदद मिलती है. कम शब्दों में कहें, तो हर लेयर, रॉ इनपुट के मुकाबले ज़्यादा जटिल और हाई-लेवल फ़ंक्शन को बेहतर तरीके से सीख रही है. अगर आपको इस बारे में ज़्यादा जानना है कि यह कैसे काम करता है, तो क्रिस ओला की बेहतरीन ब्लॉग पोस्ट देखें.
ऐक्टिवेशन के सामान्य फ़ंक्शन
आम तौर पर, ऐक्टिवेशन फ़ंक्शन के तौर पर इस्तेमाल किए जाने वाले तीन गणितीय फ़ंक्शन ये हैं: सिग्मॉइड, tanh, और ReLU.
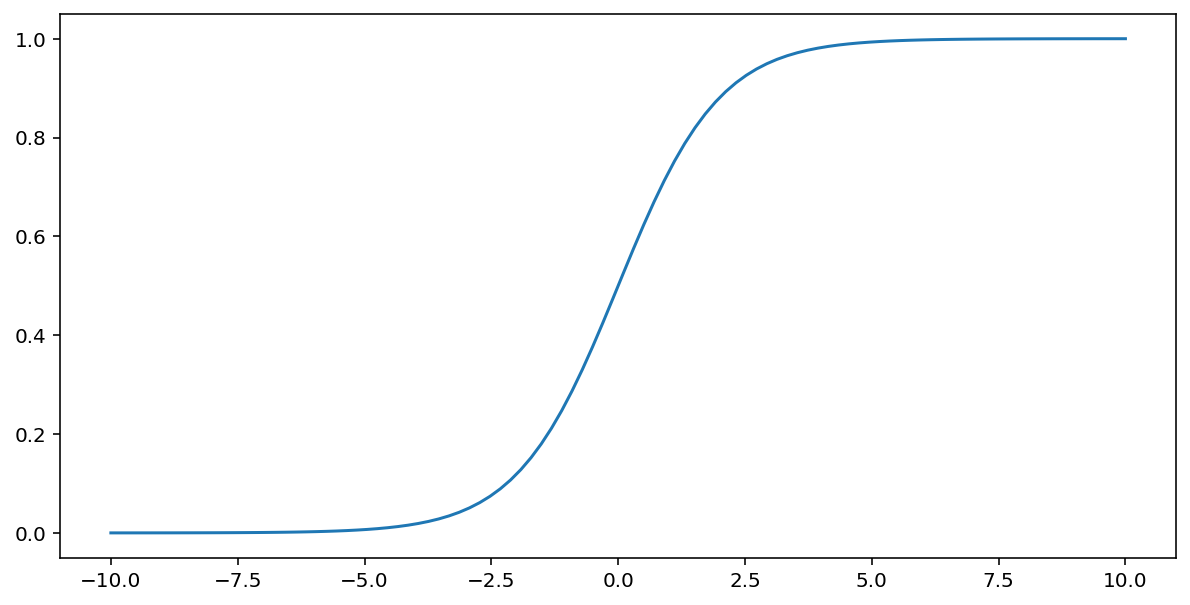
ऊपर बताए गए सिगमॉइड फ़ंक्शन, इनपुट के तौर पर दिए गए $x$ पर यह ट्रांसफ़ॉर्मेशन करता है. इससे, 0 से 1 के बीच की आउटपुट वैल्यू मिलती है:
\[F(x)=\frac{1} {1+e^{-x}}\]
यहां इस फ़ंक्शन का प्लॉट दिया गया है:
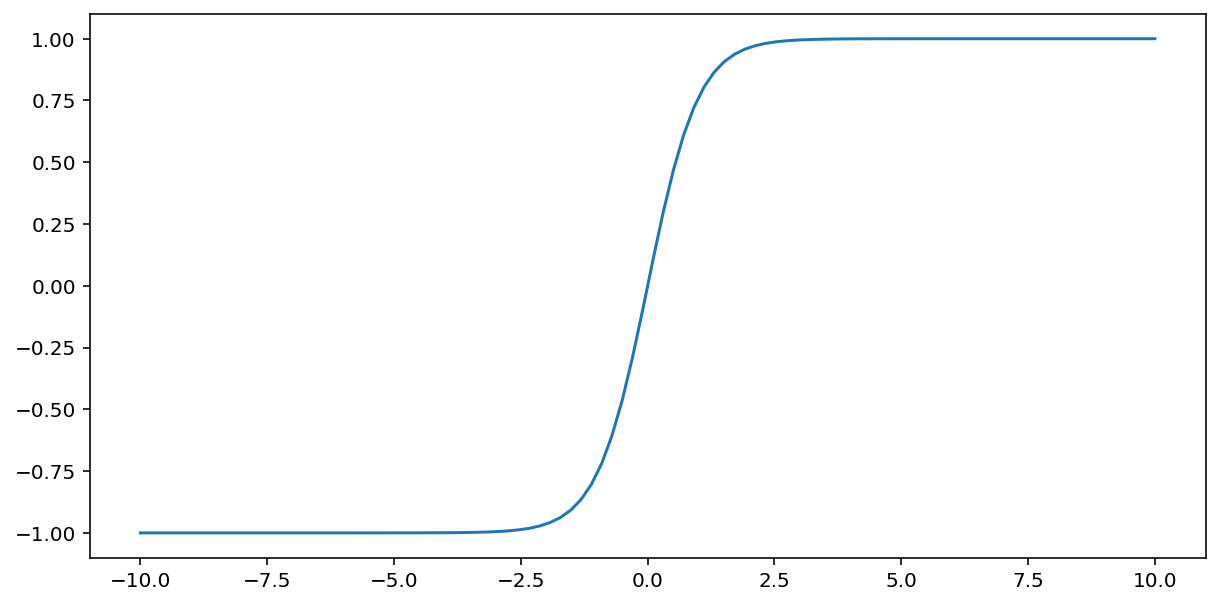
tanh ("हाइपरबॉलिक टैंजेंट" का छोटा नाम) फ़ंक्शन, इनपुट $x$ को बदलकर –1 और 1 के बीच का आउटपुट वैल्यू जनरेट करता है:
\[F(x)=tanh(x)\]
यहां इस फ़ंक्शन का प्लॉट दिया गया है:
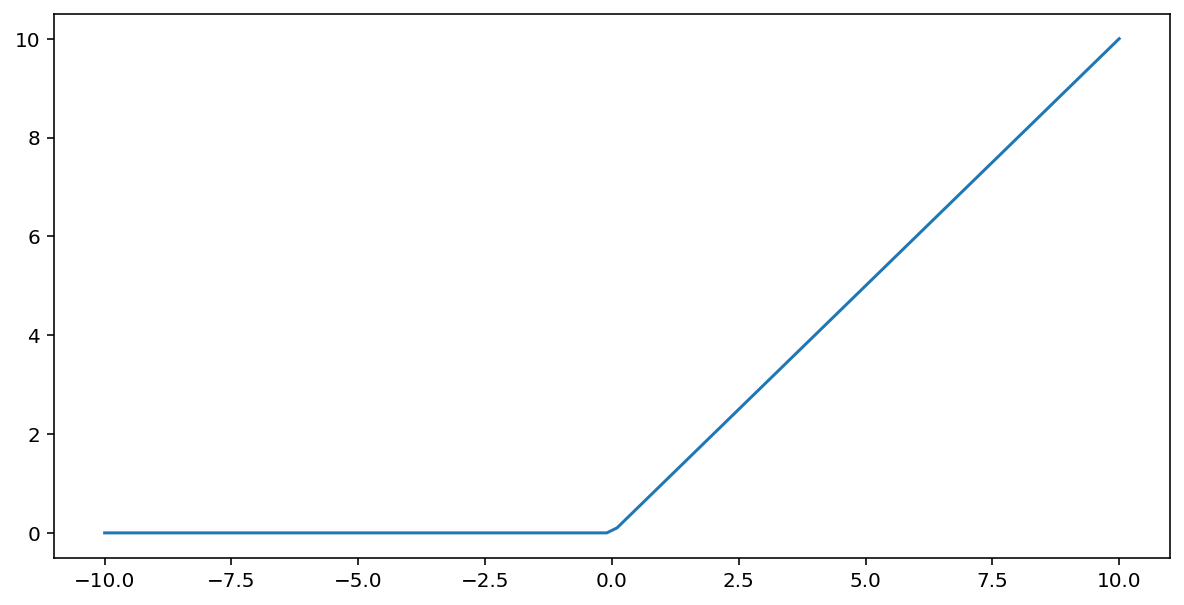
रेक्टिफ़ाइड लीनियर यूनिट ऐक्टिवेशन फ़ंक्शन (या ReLU) नीचे दिए गए एल्गोरिदम का इस्तेमाल करके आउटपुट में बदलाव करता है:
- अगर इनपुट वैल्यू $x$ 0 से कम है, तो 0 दिखाएं.
- अगर इनपुट वैल्यू $x$ 0 से ज़्यादा या उसके बराबर है, तो इनपुट वैल्यू दिखाएं.
ReLU को मैथमैटिकल तरीके से दिखाने के लिए, max() फ़ंक्शन का इस्तेमाल किया जा सकता है:
यहां इस फ़ंक्शन का प्लॉट दिया गया है:
आम तौर पर, ReLU, सिग्मॉइड या tanh जैसे स्मूद फ़ंक्शन के मुकाबले, ऐक्टिवेशन फ़ंक्शन के तौर पर थोड़ा बेहतर काम करता है. इसकी वजह यह है कि न्यूरल नेटवर्क ट्रेनिंग के दौरान, यह वैनिशिंग ग्रेडिएंट की समस्या से कम प्रभावित होता है. इन फ़ंक्शन के मुकाबले, ReLU का इस्तेमाल करना भी काफ़ी आसान है.
चालू करने के अन्य फ़ंक्शन
असल में, कोई भी गणितीय फ़ंक्शन, ऐक्टिवेशन फ़ंक्शन के तौर पर काम कर सकता है. मान लें कि \(\sigma\) हमारे चालू करने वाले फ़ंक्शन को दिखाता है. नेटवर्क में किसी नोड की वैल्यू, इस फ़ॉर्मूला से मिलती है:
Keras टूल कई तरह के ऐक्टिवेशन फ़ंक्शन के लिए, पहले से ज़्यादा सुविधाएं उपलब्ध कराता है. हालांकि, हमारा सुझाव है कि आप ReLU से शुरुआत करें.
खास जानकारी
नीचे दिए गए वीडियो में, अब तक नेटवर्क बनाने के तरीके के बारे में बताई गई सभी बातों की खास जानकारी दी गई है:
अब हमारे मॉडल में वे सभी स्टैंडर्ड कॉम्पोनेंट मौजूद हैं जिनके बारे में आम तौर पर, लोग न्यूरल नेटवर्क के तौर पर बात करते हैं:
- नोड का एक सेट, जो न्यूरॉन के जैसा होता है और जो परतों में व्यवस्थित होता है.
- वेट का एक सेट, जो हर न्यूरल नेटवर्क लेयर और उसके नीचे की लेयर के बीच के कनेक्शन को दिखाता है. इसके नीचे की लेयर, एक और न्यूरल नेटवर्क लेयर या किसी दूसरी तरह की लेयर हो सकती है.
- पक्षपात का एक सेट, हर नोड के लिए एक.
- एक ऐक्टिवेशन फ़ंक्शन, जो किसी लेयर में हर नोड के आउटपुट को बदलता है. अलग-अलग लेयर के चालू होने के फ़ंक्शन अलग-अलग हो सकते हैं.
एक चेतावनी: ज़रूरी नहीं है कि न्यूरल नेटवर्क, फ़ीचर क्रॉस से हमेशा बेहतर हों. हालांकि, न्यूरल नेटवर्क एक ऐसा विकल्प देते हैं जो कई मामलों में अच्छा काम करता है.
