Nell'esercizio precedente hai visto che l'aggiunta di livelli nascosti alla nostra rete non era sufficiente per rappresentare le non linearità. Le operazioni lineari eseguite su operazioni lineari sono ancora lineari.
Come puoi configurare una rete neurale per apprendere le relazioni non lineari tra i valori? Abbiamo bisogno di un modo per inserire operazioni matematiche non lineari in un modello.
Se questo ti sembra familiare, è perché in precedenza nel corso abbiamo applicato operazioni matematiche non lineari all'output di un modello lineare. Nel modulo Regressione logistica, abbiamo adattato un modello di regressione lineare in modo che restituisca un valore continuo compreso tra 0 e 1 (che rappresenta una probabilità) passando l'output del modello attraverso una funzione sigmoide.
Possiamo applicare lo stesso principio alla nostra rete neurale. Ripassiamo il modello dell'esercizio 2 precedente, ma questa volta, prima di emettere il valore di ogni nodo, applichiamo prima la funzione sigmoide:
Prova a eseguire la procedura passo passo dei calcoli di ogni nodo facendo clic sul pulsante >| (a destra del pulsante di riproduzione). Rivedi le operazioni matematiche eseguite per calcolare il valore di ciascun nodo nel riquadro Calcoli sotto il grafico. Tieni presente che l'output di ogni nodo ora è una trasformazione sigmoide della combinazione lineare dei nodi nello strato precedente e che i valori di output sono tutti compressi tra 0 e 1.
In questo caso, la funzione sigmoidea funge da funzione di attivazione per la rete neurale, una trasformazione non lineare del valore di output di un neurone prima che il valore venga passato come input ai calcoli dello strato successivo della rete neurale.
Ora che abbiamo aggiunto una funzione di attivazione, l'aggiunta di livelli ha un impatto maggiore. L'accumulo di non linearità ci consente di modellare relazioni molto complicate tra gli input e gli output previsti. In breve, ogni livello impara in modo efficace una funzione di livello superiore più complessa rispetto agli input non elaborati. Per saperne di più su come funziona, consulta l'eccellente post del blog di Chris Olah.
Funzioni di attivazione comuni
Tre funzioni matematiche comunemente utilizzate come funzioni di attivazione sono sigmoide, tanh e ReLU.
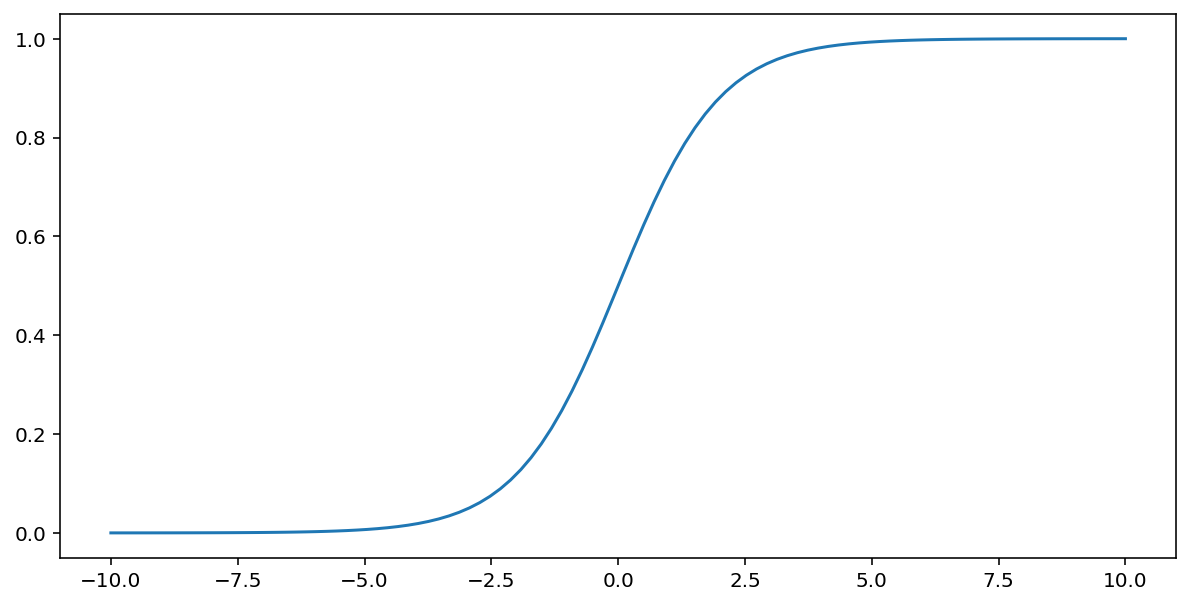
La funzione sigmoidale (discussa sopra) esegue la seguente trasformazione sull'input $x$, producendo un valore di output compreso tra 0 e 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Ecco un grafico di questa funzione:
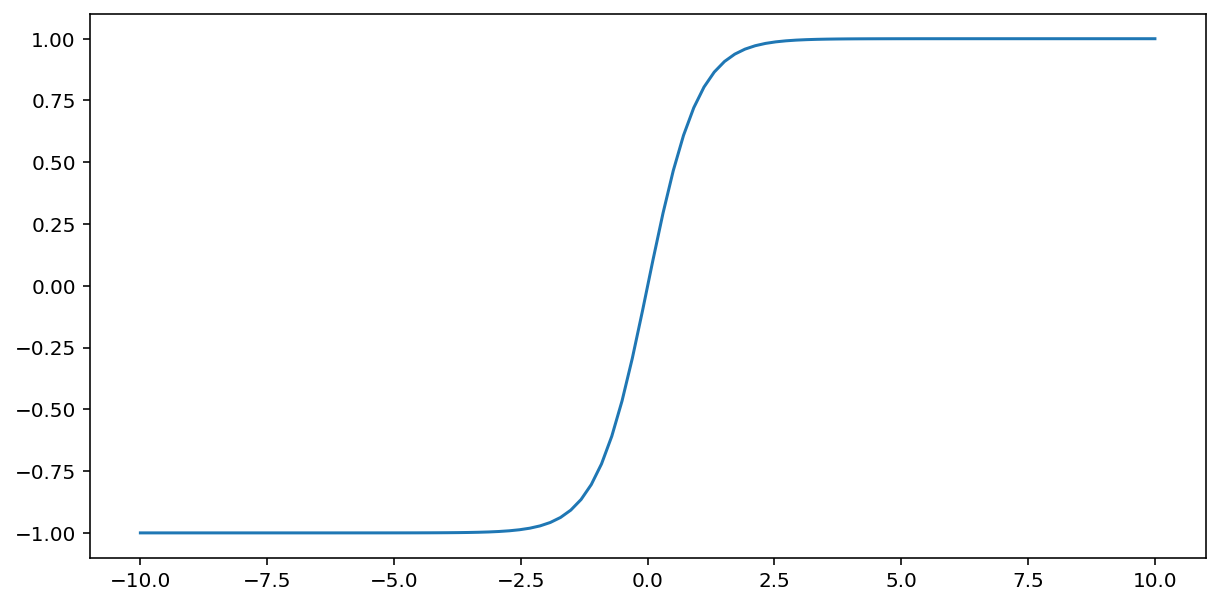
La funzione tanh (abbreviazione di "tangente iperbolica") trasforma l'input $x$ per produrre un valore di output compreso tra -1 e 1:
\[F(x)=tanh(x)\]
Ecco un grafico di questa funzione:
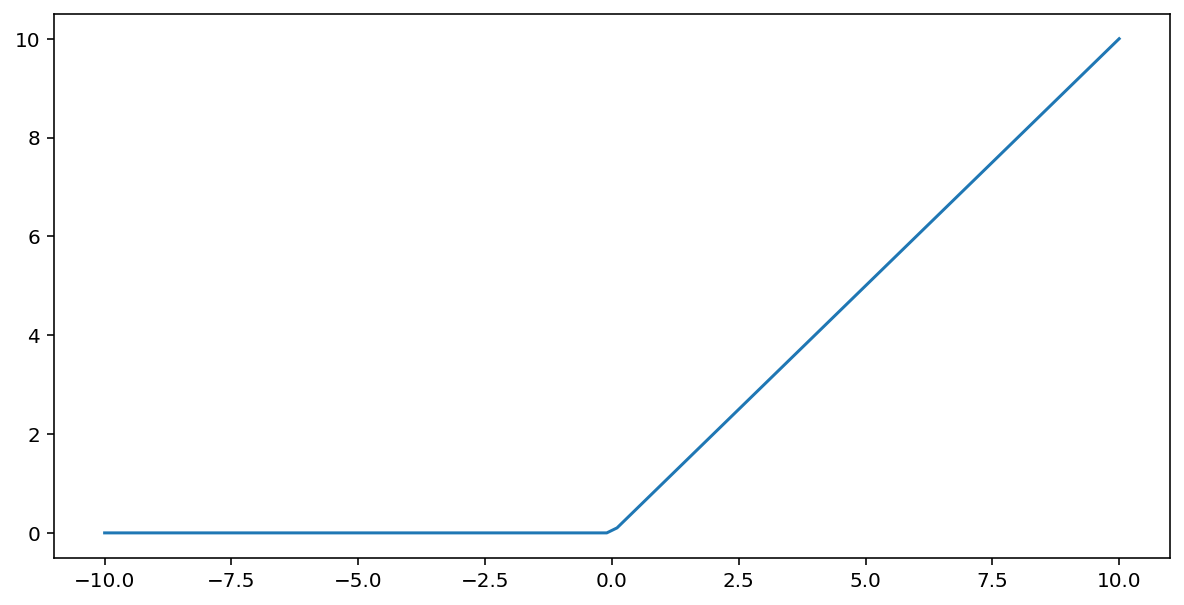
La funzione di attivazione unità lineare rettificata (o ReLU, per abbreviare) trasforma l'output utilizzando il seguente algoritmo:
- Se il valore di input $x$ è minore di 0, restituisce 0.
- Se il valore di input $x$ è maggiore o uguale a 0, restituisce il valore di input.
La funzione ReLU può essere rappresentata matematicamente mediante la funzione max():
Ecco un grafico di questa funzione:
La funzione ReLU spesso funziona un po' meglio come funzione di attivazione rispetto a una funzione fluida come sigmoidea o tanh, perché è meno suscettibile al problema di scomparsa del gradiente durante l'addestramento della rete neurale. Inoltre, la funzione ReLU è notevolmente più facile da calcolare rispetto a queste funzioni.
Altre funzioni di attivazione
In pratica, qualsiasi funzione matematica può svolgere una funzione di attivazione. Supponiamo che \(\sigma\) rappresenti la nostra funzione di attivazione. Il valore di un nodo nella rete è dato dalla seguente formula:
Keras fornisce il supporto immediato per molte funzioni di attivazione. Detto questo, consigliamo comunque di iniziare con la funzione ReLU.
Riepilogo
Il video seguente offre un riepilogo di tutto ciò che hai appreso finora sulla costruzione delle reti neurali:
Ora il nostro modello contiene tutti i componenti standard di ciò che le persone in genere intendono quando si riferiscono a una rete neurale:
- Un insieme di nodi, analoghi ai neuroni, organizzati in livelli.
- Un insieme di pesi che rappresentano le connessioni tra ogni livello della rete neurale e quello sottostante. Il livello sottostante potrebbe essere un altro livello della rete neurale o un altro tipo di livello.
- Un insieme di bias, uno per ogni nodo.
- Una funzione di attivazione che trasforma l'output di ogni nodo in uno strato. Gli strati diversi possono avere funzioni di attivazione diverse.
Un'avvertenza: le reti neurali non sono necessariamente sempre migliori degli incroci di caratteristiche, ma offrono un'alternativa flessibile che funziona bene in molti casi.
