在上一個練習中,您已瞭解在網路中加入隱藏層並不足以呈現非線性關係。對線性運算執行的線性運算仍為線性運算。
如何設定神經網路,以便學習值之間的非線性關係?我們需要某種方法,將非線性數學運算插入模型中。
如果這似乎有點熟悉,那是因為我們在課程前面已將非線性數學運算套用至線性模型的輸出結果。在「邏輯迴歸」模組中,我們調整了線性迴歸模型,透過S 函數傳遞模型輸出結果,輸出 0 到 1 的連續值 (代表機率)。
我們可以將相同原則套用至神經網路。讓我們回到練習 2 的模型,但這次在輸出每個節點的值之前,我們會先套用 S 函數:
按一下 >| 按鈕 (位於播放按鈕右側),嘗試逐步執行每個節點的計算。查看為了計算每個節點值,而執行的數學運算可在圖表下方的「Calculations」(計算) 面板中查看。請注意,現在每個節點的輸出內容都是 S 形轉換,呈現上一層節點的線性組合,且輸出值全都介於 0 和 1 之間。
在此, S 函數可做為類神經網路的啟用函式,這是神經元輸出值的輸入值之前的輸入值,之後才會將值做為輸入內容傳遞至類神經網路下一層的輸入。
現在,我們新增了啟動函式,新增圖層會產生更大影響。將非線性疊加在非線性上,可讓我們模擬輸入內容和預測輸出之間的複雜關係。簡而言之,每個層級都會有效地從原始輸入資料中學習更複雜、更高層級的函式。如想進一步瞭解這項功能的運作方式,請參閱 Chris Olah 撰寫的優質網誌文章。
常見的活化函式
常用做為活化函式的三個數學函式是 sigmoid、tanh 和 ReLU。
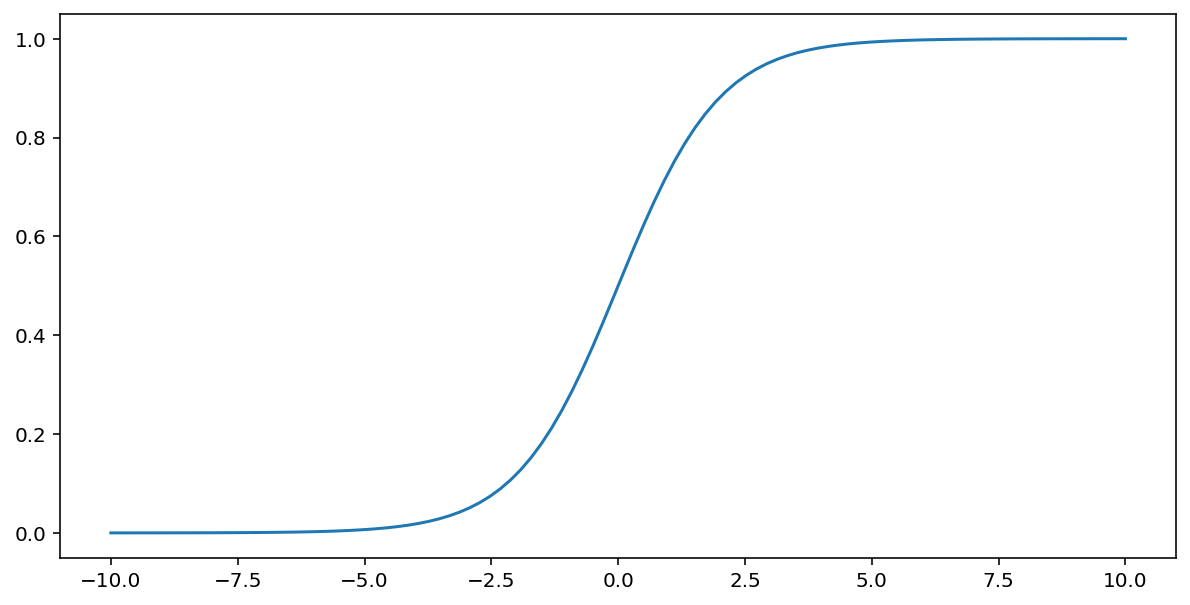
上述所述的 S 函數會對輸入 $x$ 執行以下轉換,產生介於 0 和 1 之間的輸出值:
\[F(x)=\frac{1} {1+e^{-x}}\]
這個函式的圖表如下:
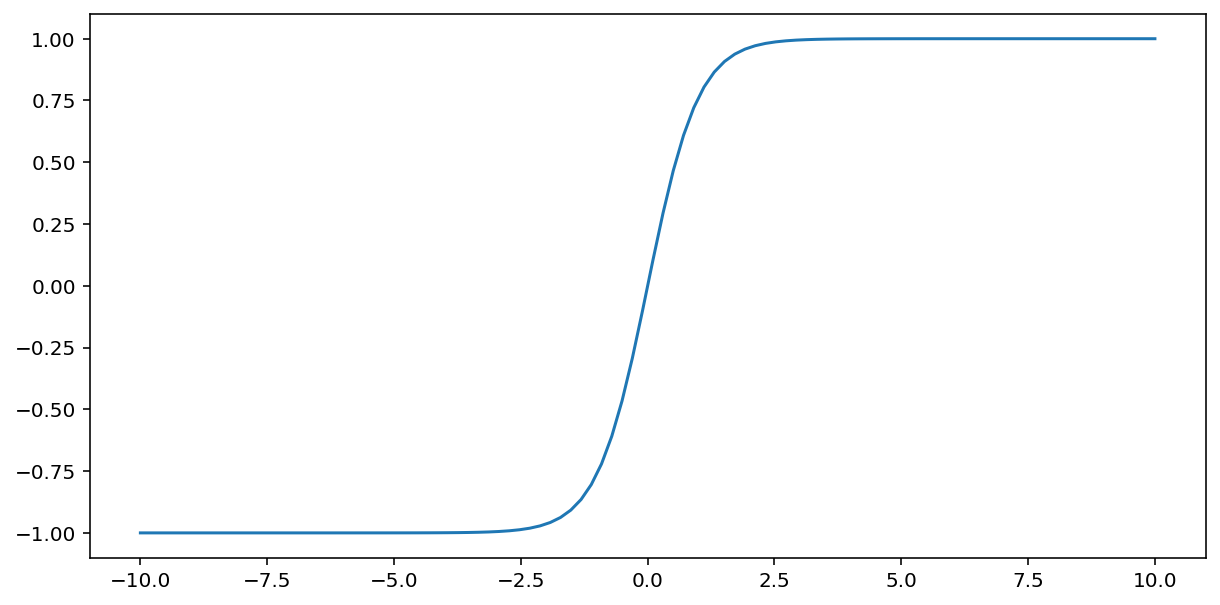
Tanh (「雙曲正切」的縮寫) 函式會轉換輸入 $x$ 以產生介於 –1 與 1 之間的輸出值:
\[F(x)=tanh(x)\]
這個函式的圖表如下:
Rectified Linear Unit 活化函式 (簡稱 ReLU) 會使用下列演算法轉換輸出內容:
- 如果輸入值 $x$ 小於 0,則傳回 0。
- 如果輸入值 $x$ 大於或等於 0,則傳回輸入值。
您可以使用 max() 函式以數學方式表示 ReLU:
這個函式的圖表如下:
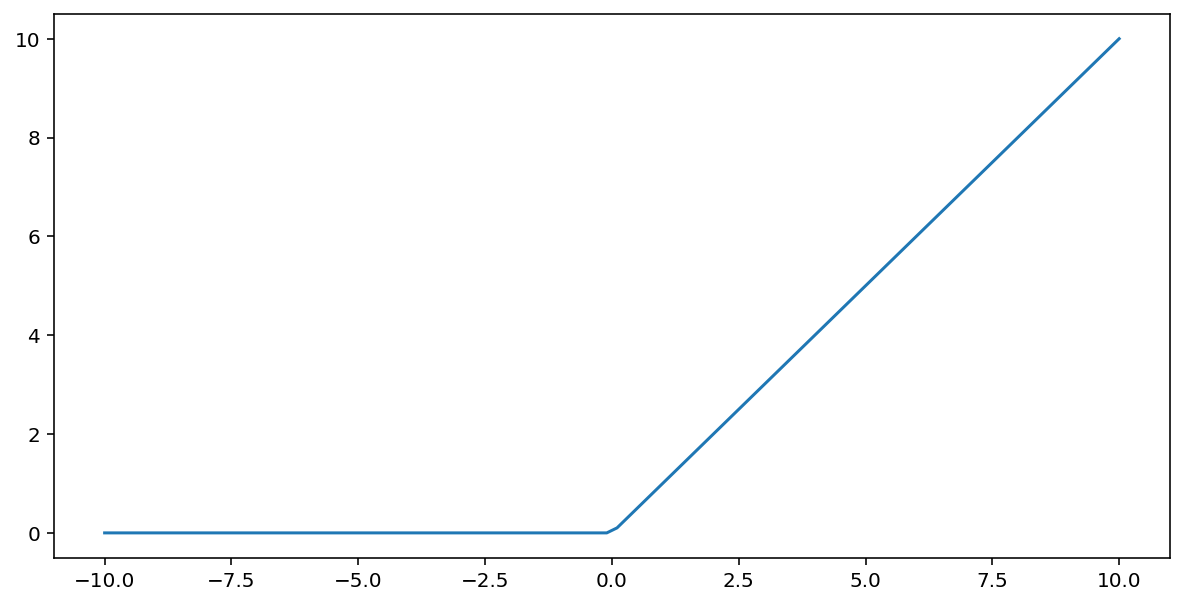
與 sigmoid 或 tanh 等平滑函式相比,ReLU 通常更適合作為激活函式,因為它較不易受到神經網路訓練期間梯度消失問題的影響。ReLU 的運算也比這些函式容易許多。
其他啟用函式
在實務上,任何數學函式都可以做為活化函數。假設 \(\sigma\) 代表我們的激活函式。網路中節點的值可由下列公式計算:
Keras 為許多啟用函式提供立即可用的支援。儘管如此,我們仍建議先從 ReLU 著手。
摘要
以下影片回顧您目前為止學到的所有知識,瞭解類神經網路的建構方式:
現在,我們的模型含有人們參照類神經網路時通常意思的所有標準元件:
- 一組類似神經元的節點,以分層方式排列。
- 一組權重,代表各個神經網路層與其下層之間的連結。下方的層可能是另一個神經網路層,或其他類型的層。
- 一組偏差值,每個節點各一個。
- 此激活函式會轉換層中每個節點的輸出內容。不同的圖層可能有不同的活化函式。
注意:類神經網路不一定比特徵交叉更優越,但在許多情況下,類神經網路確實提供了靈活的替代方案。
