您在上一个练习中了解到,仅向网络添加隐藏层不足以表示非线性关系。对线性运算执行的线性运算仍然是线性的。
如何配置神经网络来学习值之间的非线性关系?我们需要找到一种将非线性数学运算插入模型的方法。
如果这看起来有点熟悉,那是因为我们在本课程的早些部分实际上就对线性模型的输出应用了非线性数学运算。在逻辑回归模块中,我们通过将模型的输出通过 S 型函数传递,使线性回归模型输出介于 0 到 1 之间的连续值(表示概率)。
我们可以将同样的原则应用于神经网络。我们来回顾一下之前的练习 2 中的模型,不过这次,在输出每个节点的值之前,我们先应用 S 型函数:
您可以点击 >| 按钮(位于播放按钮右侧),逐步执行每个节点的计算。在图表下方的计算面板中,查看计算每个节点值所执行的数学运算。请注意,每个节点的输出现在是上一层节点线性组合的 sigmoid 转换,并且输出值均压缩在 0 到 1 之间。
在这里,S 型函数用作神经网络的激活函数,用于对神经元的输出值进行非线性转换,然后将该值作为输入传递给神经网络下一层的计算。
现在,我们添加了激活函数,添加层会产生更大的影响。通过将非线性叠加到非线性上,我们可以对输入和预测输出之间的非常复杂的关系进行建模。简而言之,每一层都会针对原始输入有效地学习更复杂、更高级别的函数。如果您想更直观地了解其运作方式,请参阅 Chris Olah 的优秀博文。
常用激活函数
常用作激活函数的三个数学函数是 Sigmoid 函数、tanh 函数和 ReLU 函数。
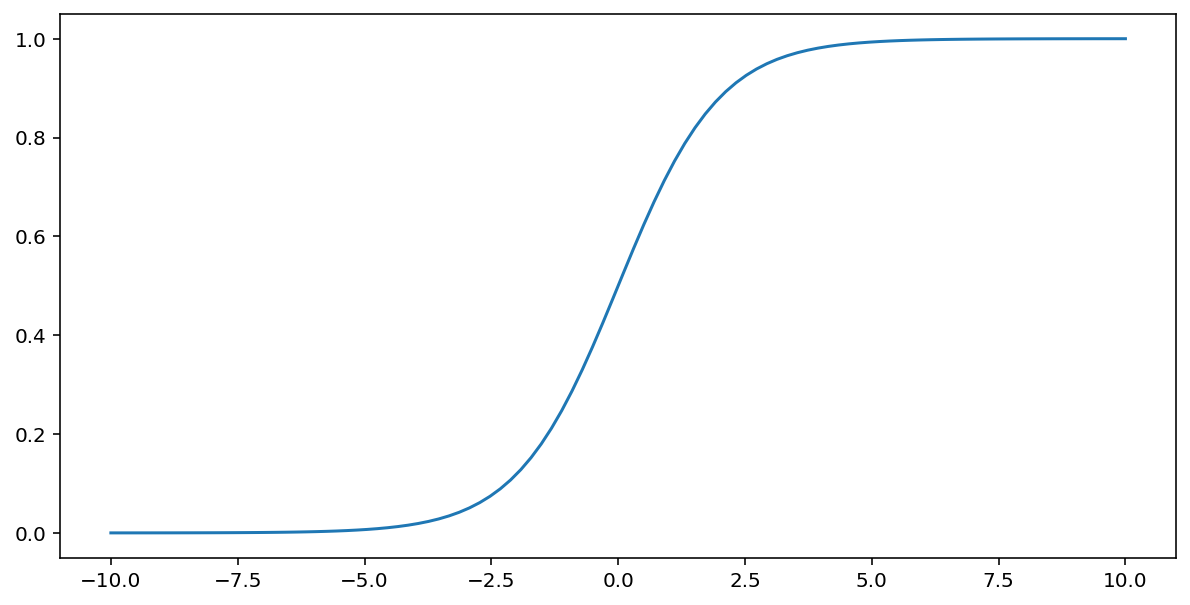
S 型函数(如上文所述)对输入 $x$ 执行以下转换,从而生成一个介于 0 到 1 之间的输出值:
\[F(x)=\frac{1} {1+e^{-x}}\]
下面是该函数的图表:
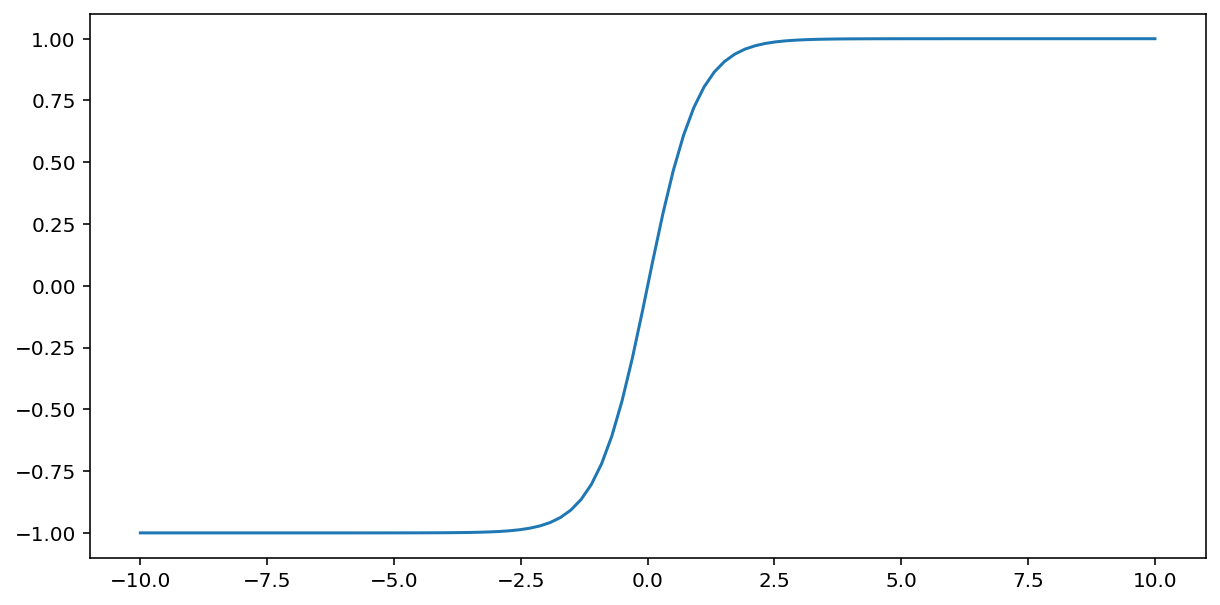
tanh(简称“双曲正切”)函数会转换输入 $x$,以生成介于 -1 和 1 之间的输出值:
\[F(x)=tanh(x)\]
以下是此函数的图表:
修正线性单元激活函数(简称 ReLU)使用以下算法转换输出:
- 如果输入值 $x$ 小于 0,则返回 0。
- 如果输入值 $x$ 大于或等于 0,则返回输入值。
可以使用 max() 函数以数学方式表示 ReLU:
下面是该函数的图表:
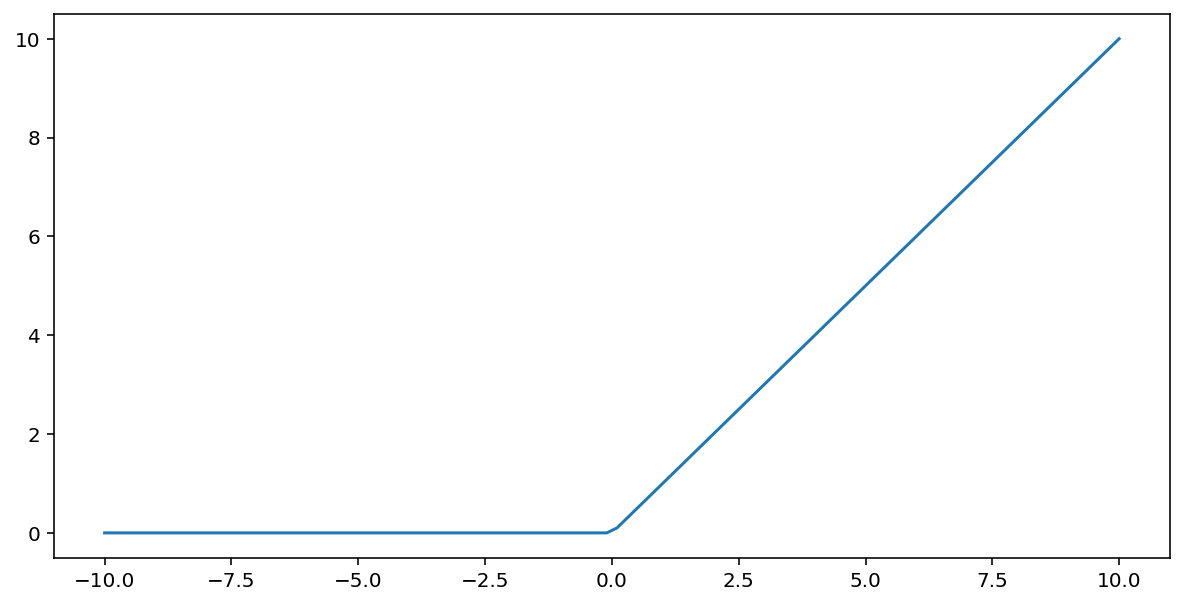
ReLU 作为激活函数的效果通常优于 S 型函数或 tanh 等平滑函数,因为它在神经网络训练期间不易受到梯度消失问题的影响。与这些函数相比,ReLU 的计算也更容易。
其他激活函数
在实践中,任何数学函数都可以用作激活函数。假设 \(\sigma\) 代表我们的激活函数。网络中节点的值由以下公式给出:
Keras 为许多激活函数提供开箱即用型支持。尽管如此,我们仍建议您先从 ReLU 开始。
摘要
以下视频回顾了您迄今为止学到的有关神经网络构建方式的所有内容:
现在,我们的模型包含人们通常在提及神经网络时所指的所有标准组件:
- 一组节点,类似于神经元,并且位于层中。
- 一组权重,表示每个神经网络层与其下方的层之间的关系。下方的层可能是另一个神经网络层,也可能是其他类型的层。
- 一组偏差,每个节点一个偏差。
- 一个激活函数,对层中每个节点的输出进行转换。不同的层可能拥有不同的激活函数。
警告:神经网络不一定总比特征组合好,但神经网络确实可以提供一种灵活的替代方案,在许多情况下效果都很好。
