Você viu no exercício anterior que apenas adicionar camadas ocultas à nossa rede não era suficiente para representar não linearidades. As operações lineares realizadas em operações lineares ainda são lineares.
Como você pode configurar uma rede neural para aprender relacionamentos não lineares entre valores? Precisamos de uma maneira de inserir operações matemáticas não lineares em um modelo.
Se isso parece familiar, é porque aplicamos operações matemáticas não lineares à saída de um modelo linear no início do curso. No módulo Regressão logística, adaptamos um modelo de regressão linear para gerar um valor contínuo de 0 a 1 (que representa uma probabilidade) transmitindo a saída do modelo por uma função sigmoide.
Podemos aplicar o mesmo princípio à nossa rede neural. Vamos revisitar nosso modelo do Exercício 2 anterior, mas desta vez, antes de gerar o valor de cada nó, vamos aplicar a função sigmoide:
Tente passar pelos cálculos de cada nó clicando no botão >| (à direita do botão de reprodução). Revise as operações matemáticas realizadas para calcular cada valor de nó no painel Cálculos abaixo do gráfico. A saída de cada nó agora é uma transformação sigmoide da combinação linear dos nós na camada anterior, e os valores de saída são todos comprimidos entre 0 e 1.
Aqui, a sigmoide serve como uma função de ativação para a rede neural, uma transformação não linear do valor de saída de um neurônio antes que o valor seja transmitido como entrada para os cálculos da próxima camada da rede neural.
Agora que adicionamos uma função de ativação, adicionar camadas tem mais impacto. A sobreposição de não linearidades permite modelar relações muito complicadas entre as entradas e as saídas previstas. Em resumo, cada camada está aprendendo uma função mais complexa e de nível mais alto sobre as entradas brutas. Para entender melhor como isso funciona, consulte a excelente postagem do blog de Chris Olah (em inglês).
Funções de ativação comuns
Três funções matemáticas que são comumente usadas como funções de ativação são sigmoid, tanh e ReLU.
A função sigmoide (discutida acima) executa a seguinte transformação na entrada $x$, produzindo um valor de saída entre 0 e 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Confira o gráfico dessa função:
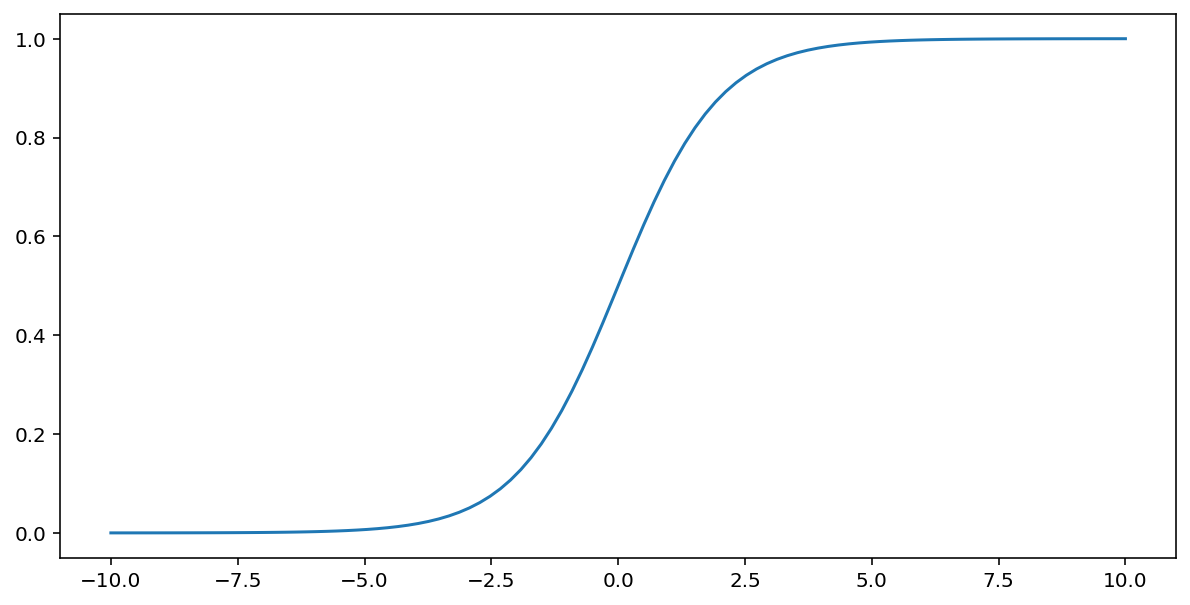
A função tanh (abreviação de "tangente hiperbólica") transforma a entrada $x$ para produzir um valor de saída entre –1 e 1:
\[F(x)=tanh(x)\]
Confira um gráfico dessa função:
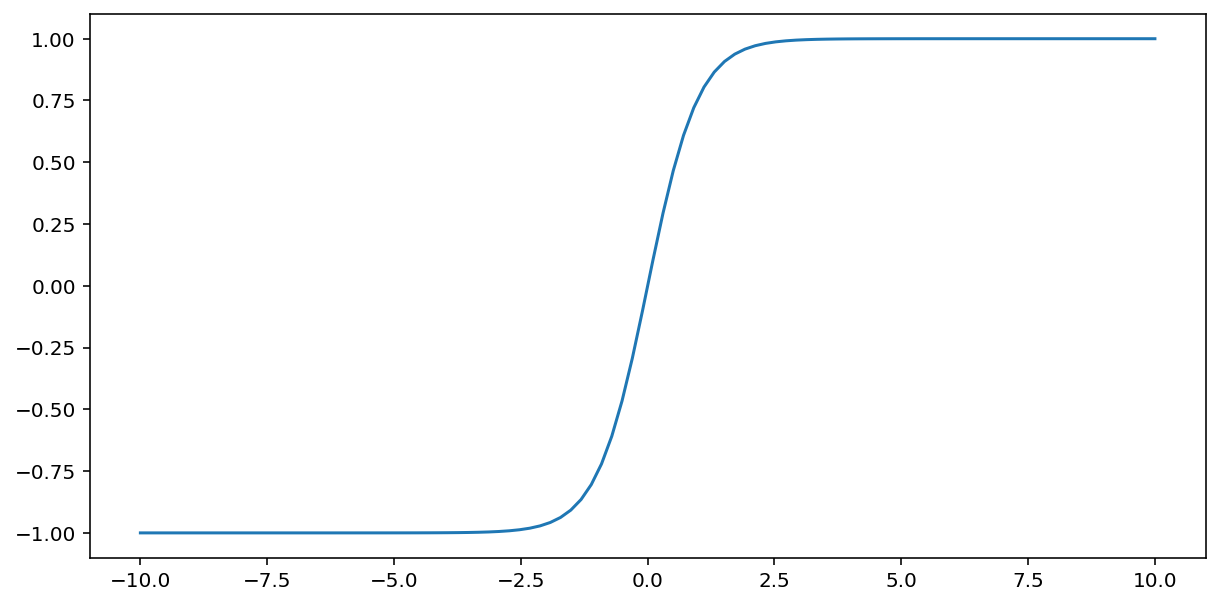
A função de ativação da unidade linear retificada (ou ReLU, em resumo) transforma a saída usando o seguinte algoritmo:
- Se o valor de entrada $x$ for menor que 0, retornará 0.
- Se o valor de entrada $x$ for maior ou igual a 0, retorne o valor de entrada.
A ReLU pode ser representada matematicamente usando a função max():
Confira um gráfico dessa função:
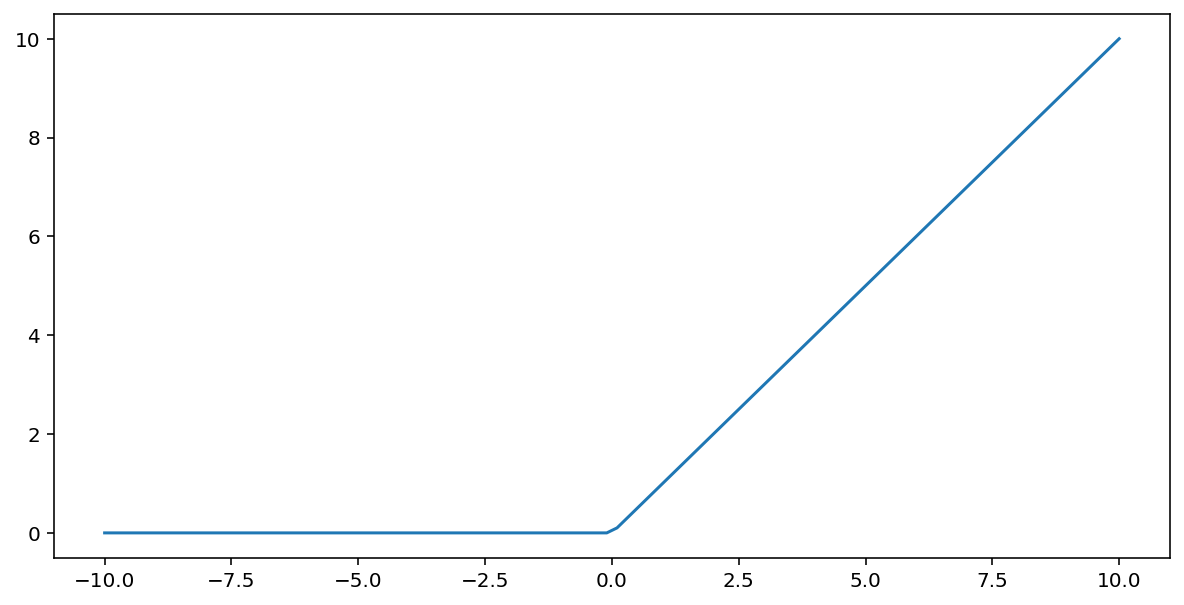
A ReLU geralmente funciona um pouco melhor como uma função de ativação do que uma função suave, como sigmoide ou tanh, porque é menos suscetível ao problema de gradiente nulo durante o treinamento de rede neural. A ReLU também é muito mais fácil de calcular do que essas funções.
Outras funções de ativação
Na prática, qualquer função matemática pode servir como uma função de ativação. Suponha que \(\sigma\) represente nossa função de ativação. O valor de um nó na rede é dado pela seguinte fórmula:
O Keras oferece suporte pronto para uso a muitas funções de ativação. No entanto, ainda recomendamos começar com ReLU.
Resumo
O vídeo a seguir fornece uma recapitulação de tudo o que você aprendeu até agora sobre como as redes neurais são construídas:
Agora nosso modelo tem todos os componentes padrão do que as pessoas geralmente se referem quando mencionam uma rede neural:
- Um conjunto de nós, análogos aos neurônios, organizados em camadas.
- Um conjunto de pesos que representam as conexões entre cada camada da rede neural e a camada abaixo dela. A camada abaixo pode ser outra camada de rede neural ou algum outro tipo de camada.
- Um conjunto de vieses, um para cada nó.
- Uma função de ativação que transforma a saída de cada nó em uma camada. Camadas diferentes podem ter funções de ativação distintas.
Uma ressalva: as redes neurais nem sempre são melhores que os cruzamentos de atributos, mas oferecem uma alternativa flexível que funciona bem em muitos casos.
