З попередньої вправи ви дізналися, що простого додавання прихованих шарів до мережі недостатньо, щоб представити нелінійності. Лінійні операції, які виконуються з операціями такого самого типу, залишаються лінійними.
Як налаштувати нейронну мережу для вивчення нелінійних зв’язків між значеннями? Потрібно якось вставити нелінійні математичні операції в модель.
Це може здаватися дещо знайомим, тому що раніше в цьому курсі ми фактично застосовували нелінійні математичні операції до вихідних даних лінійної моделі. У модулі Логістична регресія ми адаптували модель лінійної регресії, щоб вона виводила неперервне значення від 0 до 1 (що представляє імовірність), пропускаючи вихідні дані через сигмоїдну функцію.
Можна застосувати той самий принцип до нейронної мережі. Повернімося до моделі з вправи 2, але цього разу, перш ніж виводити значення кожного вузла, спочатку застосуймо сигмоїдну функцію.
Спробуйте обчислити кожен вузол, натискаючи >| (праворуч від кнопки запуску). Перегляньте математичні операції, за допомогою яких обчислено кожне значення вузла. Їх наведено в розділі Calculations (Обчислення) під графіком. Зверніть увагу, що вихідні дані кожного вузла тепер є сигмоїдним перетворенням лінійної комбінації вузлів із попереднього шару, а всі вихідні значення розміщуються між 0 і 1.
Тут сигмоїда служить функцією активації для нейронної мережі, яка виконує нелінійне перетворення вихідного значення нейрона, перш ніж воно надійде як вхідні дані на наступний шар нейронної мережі для обчислень.
З функцією активації додавання шарів більше впливає на модель. Штабелювання нелінійностей на нелінійностях дає змогу моделювати дуже складні зв’язки між вхідними даними й прогнозними результатами. Якщо коротко, то кожен шар ефективно вивчає складнішу функцію вищого рівня на необроблених вхідних даних. Якщо ви хочете краще зрозуміти, як це працює, перегляньте чудову публікацію блогу Кріса Ола.
Типові функції активації
Три математичні функції, які зазвичай використовуються для активації: сигмоїда, тангенс і ReLU.
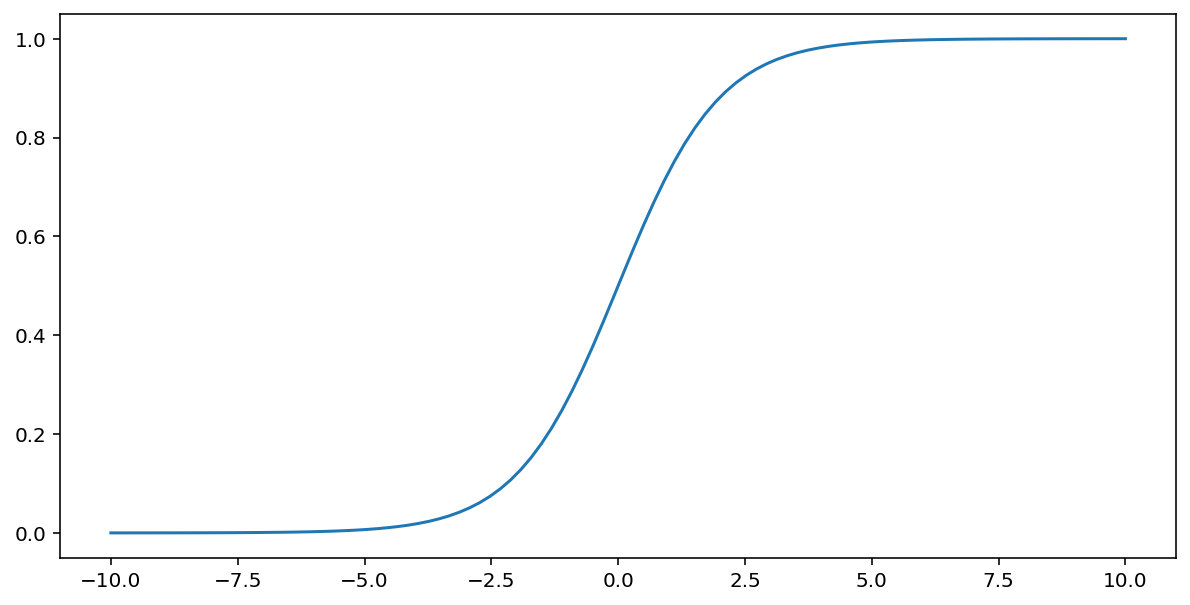
Сигмоїдна функція (про яку йшлося вище) перетворює вхідні дані за формулою, наведеною нижче, утворюючи вихідне значення від 0 до 1.
\[F(x)=\frac{1} {1+e^{-x}}\]
Ось графік цієї функції:
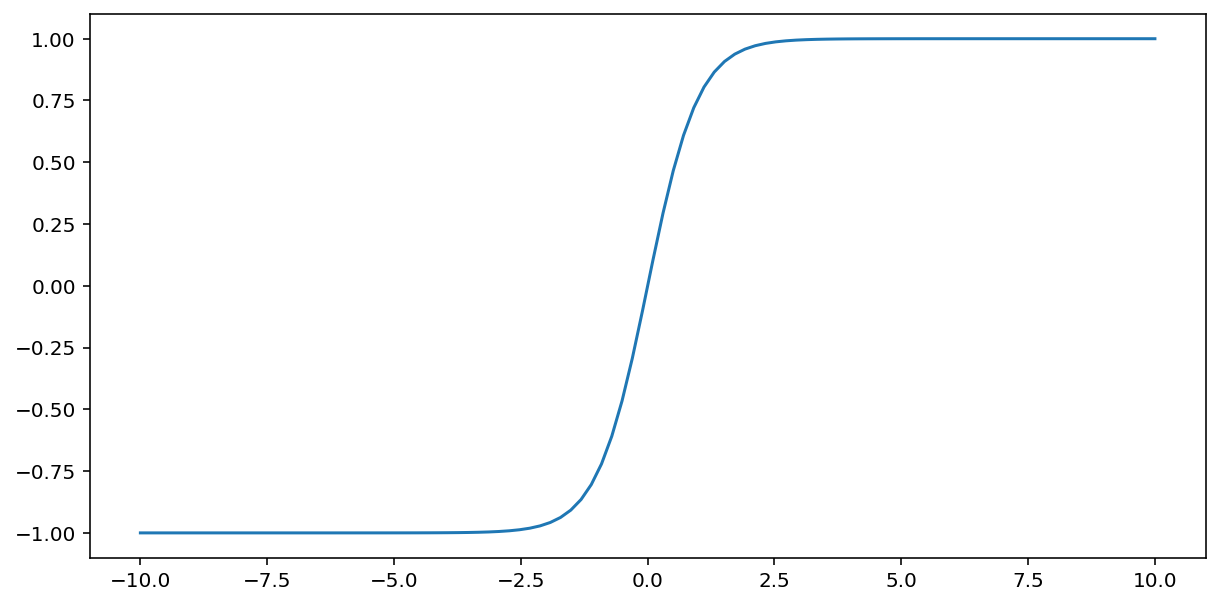
Функція тангенс (повна назва – "гіперболічний тангенс") перетворює вхідні дані, утворюючи вихідне значення від –1 до 1:
\[F(x)=tanh(x)\]
Ось графік цієї функції:
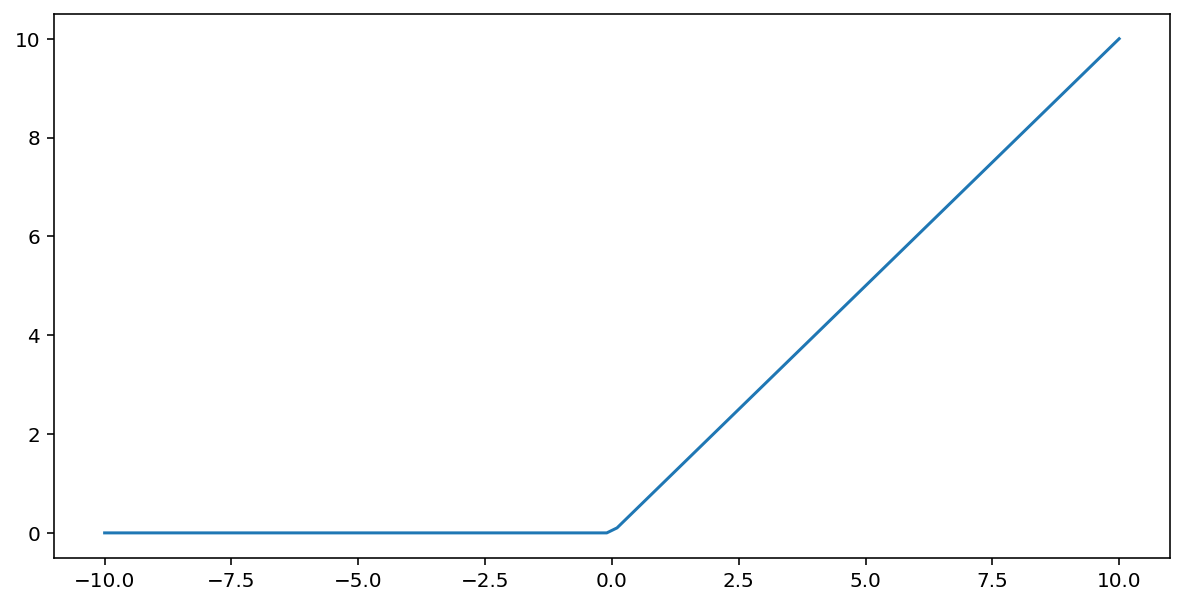
Функція активації випрямленого лінійного вузла (скорочено – ReLU) перетворює вихідні дані за таким алгоритмом:
- Якщо вхідне значення $x$ менше ніж 0, повертається 0.
- Якщо вхідне значення $x$ більше ніж 0 або дорівнює йому, повертається саме воно.
ReLU можна представити математично за допомогою функції max():
Ось графік цієї функції:
ReLU часто працює трохи краще як функція активації, ніж плавна функція, зокрема сигмоїда або тангенс, тому що вона менш чутлива до проблеми зникання градієнтів під час навчання нейронної мережі. Крім того, ReLU значно легше обчислити, ніж ці функції.
Інші функції активації
На практиці будь-яка математична функція може використовуватися для активації. Припустімо, що \(\sigma\) представляє нашу функцію активації. Значення вузла в мережі визначається за такою формулою:
Keras надає готові рішення для підтримки багатьох функцій активації. Проте ми все одно рекомендуємо починати з ReLU.
Підсумок
Це відео містить підсумок усього, що ви дізналися про те, як будуються нейронні мережі:
Тепер наша модель містить усі стандартні компоненти, які зазвичай мають на увазі, коли говорять про нейронну мережу:
- ряд вузлів, аналогічних нейронам, які розміщено на різних шарах;
- ряд значень ваги, що представляють зв’язки між кожним шаром нейронної мережі й шаром, розміщеним нижче (це може бути ще один шар нейронної мережі або шар іншого типу);
- ряд значень зсуву, по одному для кожного вузла;
- функцію активації, яка перетворює вихідне значення кожного вузла на шар (різні шари можуть мати відмінні функції активації).
Застереження: нейронні мережі не завжди кращі за поєднання ознак, але це дійсно гнучка альтернатива, яка часто добре працює.