Réseaux de neurones: classification à classes multiples

Plus tôt, vous avez rencontré classification binaire qui pouvaient choisir entre l'une des deux options possibles, par exemple:

• Un e-mail donné est considéré comme du spam ou non.
• Une tumeur donnée est maligne ou bénigne.

Dans cette section, nous étudierons classification à classes multiples qui peuvent choisir parmi plusieurs possibilités. Exemple :

• Ce chien est-il un beagle, un basset ou un limier ?
• Cette fleur est-elle un iris de Sibérie, un iris de Pays-Bas, un iris pavillon bleu, ou un iris barbu nain ?
• S'agit-il d'un Boeing 747, d'un Airbus 320, d'un Boeing 777 ou d'un Embraer 190 ?
• Cette image représente-t-elle une pomme, un ours, des bonbons, un chien ou un œuf ?

Certains problèmes à plusieurs classes concrets impliquent de choisir parmi des millions de classes distinctes. Prenons l'exemple d'une classification à classes multiples capable d'identifier l'image de tout ou partie.

Cette section décrit les deux principales variantes de la classification à classes multiples:

• un contre tous
• one-vs.-one, généralement appelé softmax

Un contre tous

Un contre tous permet d'utiliser la classification binaire pour obtenir une série de prédictions oui ou non pour plusieurs étiquettes possibles.

Pour un problème de classification avec N solutions possibles, la méthode un contre tous solution se compose de N classificateurs binaires distincts (un binaire). classificateur pour chaque résultat possible. Pendant l'entraînement, le modèle s'exécute à l'aide d'une séquence de classificateurs binaires, chacun étant entraîné pour répondre à une de classification.

Par exemple, pour l'image d'un fruit, quatre différents programmes de reconnaissance peuvent être entraînés, chacun répondant Question:

1. Cette image représente-t-elle une pomme ?
2. Cette image est-elle orange ?
3. Cette image représente-t-elle une banane ?
4. Cette image représente-t-elle un raisin ?

L'image suivante illustre comment cela fonctionne dans la pratique.

<ph type="x-smartling-placeholder">

</ph> Figure 7 Image d'une poire transmise en tant qu'entrée à quatre images différentes les classificateurs binaires. Les premier, deuxième et quatrième modèles (prédiction si l'image est une pomme, une orange ou un raisin, respectivement) pour prédire la classe négative. Le troisième modèle (prédire si oui ou non l'image est une poire) prédit la classe positive.

Pour en savoir plus sur la manière dont les classificateurs binaires effectuent des prédictions (définir un seuil de classification pour convertir la sortie du modèle numérique en une étiquette positive ou négative), consultez la Classification de ce module.

Cette approche est assez raisonnable lorsque le nombre total de classes est faible, mais devient de plus en plus inefficace à mesure que le nombre de classes augmente.

Nous pouvons créer un modèle un contre tous beaucoup plus efficace avec un réseau de neurones profond, dans lequel chaque nœud de sortie représente . L'image suivante illustre cette approche.

<ph type="x-smartling-placeholder">

</ph> Figure 8 Les mêmes tâches de classification un contre tous effectuées à l'aide d'une fonction de réseau de neurones. Une fonction d'activation sigmoïde est appliquée à la sortie. et chaque valeur de sortie représente la probabilité que l'entrée image est un fruit spécifié. Ce modèle prédit qu'il y a 84% de probabilité que l'image soit une poire et de 7% de probabilité que l'image soit raisin.

Un contre un (softmax)

Vous avez peut-être remarqué que les valeurs de probabilité dans la couche de sortie de la Figure 8 n'est pas égale à 1 (ou 100%). (en fait, leur somme est égale à 1,43). Dans une relation un contre tous la probabilité de chaque ensemble binaire de résultats est déterminée indépendamment de tous les autres ensembles. Autrement dit, nous déterminons la probabilité de "pomme" et "pas pomme" sans tenir compte de la probabilité que nos autres options de fruits : "orange", "poire" ou "raisin".

Et si nous voulions prédire les probabilités pour chaque fruit les uns par rapport aux autres ? Ici, au lieu de prédire "pomme" et non "apple", nous voulons prédire "apple" par rapport à "orange" et "poire" et "raisin". Ce type de classification à classes multiples est appelé classification un contre un.

Nous pouvons implémenter une classification de type un contre un en utilisant le même type de architecture réseau utilisée pour la classification un contre tous, avec un changement majeur. Nous devons appliquer une autre transformation à la couche de sortie.

Dans l'approche un contre tous, nous avons appliqué la fonction d'activation sigmoïde à chaque sortie. indépendamment les uns des autres, ce qui génère une valeur de sortie comprise entre 0 et 1 pour chaque nœud. mais n'a pas garanti que la somme de ces valeurs soit exactement égale à 1.

Pour un contre un, nous pouvons plutôt appliquer une fonction appelée softmax, qui attribue des probabilités décimales à chaque classe d'un problème à classes multiples de sorte que : la somme de toutes les probabilités est égale à 1,0. Cette contrainte supplémentaire contribue à la convergence de l'entraînement plus rapidement qu'auparavant.

Cliquez sur l'icône plus pour afficher l'équation softmax.

L'équation softmax est la suivante:

$$p(y = j|\textbf{x}) = \frac{e^{(\textbf{w}_j^{T}\textbf{x} + b_j)}}{\sum_{k\in K} {e^{(\textbf{w}_k^{T}\textbf{x} + b_k)}} }$$

Notez que cette formule étend la formule de la logistique logistique en plusieurs classes.

L'image suivante réimplémente notre classification à classes multiples "un contre tous" en tant que tâche un contre un. Notez que pour exécuter la fonction softmax, qui précède directement la couche de sortie (appelée couche softmax) doit avoir le même nombre de nœuds que la couche de sortie.

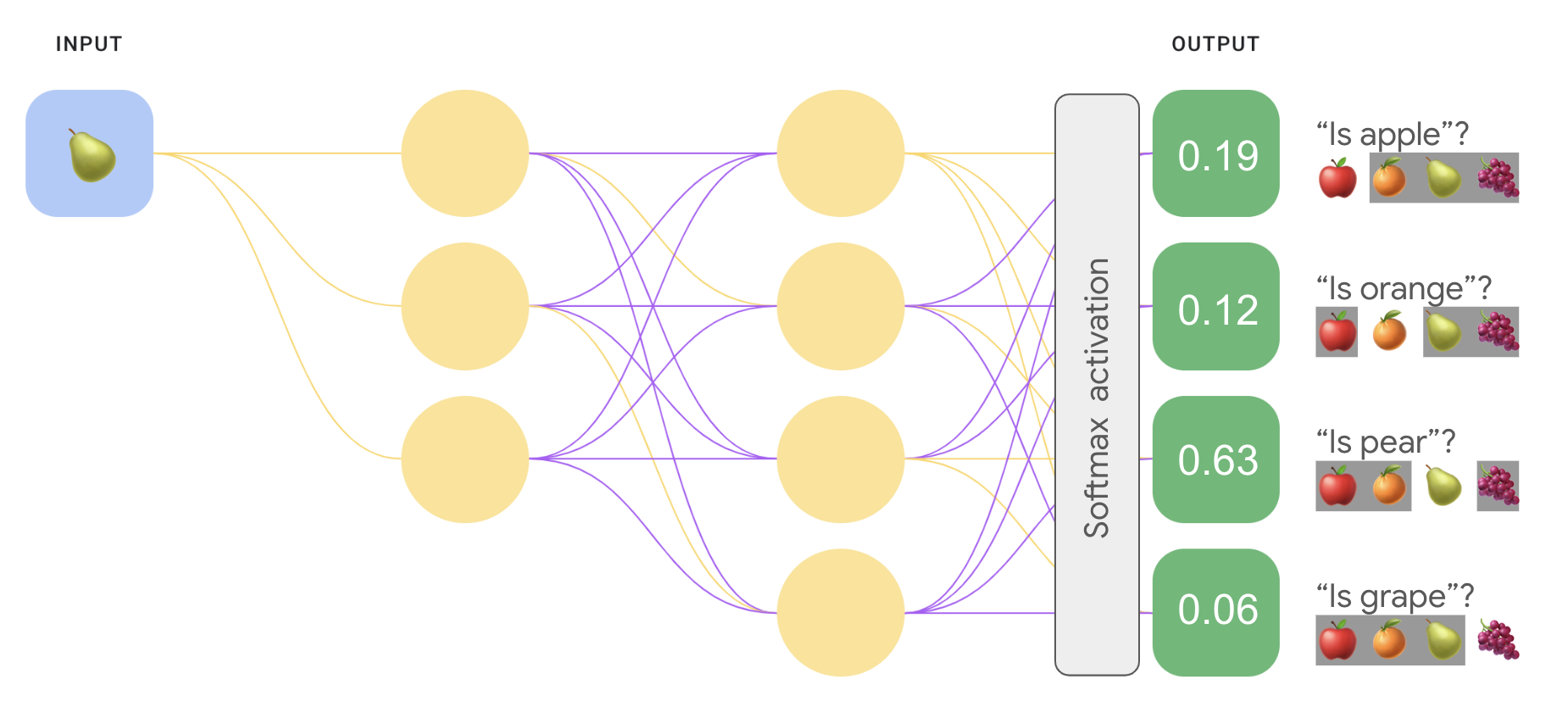<ph type="x-smartling-placeholder">

</ph> Figure 9 Implémentation d'un réseau de neurones d'une classification un contre un une couche softmax. Chaque valeur de sortie représente la probabilité que le l'image d'entrée correspond au fruit spécifié et non à l'un des trois autres fruits (la somme de toutes les probabilités est égale à 1). Ce modèle prédit qu'il y a 63% il y a peu de chances qu'il s'agisse d'une poire.

Options softmax

Prenons les variantes suivantes de softmax:

• La softmax complète est la softmax dont nous avons parlé. c'est-à-dire softmax calcule une probabilité pour chaque classe possible.

• L'échantillonnage de candidats signifie que softmax calcule une probabilité pour toutes les étiquettes positives, mais seulement pour un échantillon aléatoire étiquettes négatives. Par exemple, si nous souhaitons déterminer qu'une image d'entrée soit un beagle ou un limier, nous n'avons pas à fournissent des probabilités pour chaque exemple non chien.

La fonction softmax complète est relativement peu coûteuse lorsque le nombre de classes est faible mais il devient extrêmement coûteux lorsque le nombre de classes augmente. L'échantillonnage de candidats peut améliorer l'efficacité des problèmes ayant un grand le nombre de classes.

Une ou plusieurs étiquettes

Softmax suppose que chaque exemple appartient exactement à une classe. Cependant, certains exemples peuvent appartenir simultanément à plusieurs classes. Pour ces exemples:

• Vous ne pouvez pas utiliser softmax.
• Vous devez vous appuyer sur plusieurs régressions logistiques.

Par exemple, le modèle un contre un de la figure 9 ci-dessus suppose que chaque entrée représente exactement un type de fruit: une pomme, une orange, une poire ou un raisin. Toutefois, si une image d'entrée peut contenir plusieurs types de fruits, une de pommes et d'oranges, vous devrez utiliser plusieurs des régressions et des régressions.

Termes clés:

• Classification binaire
• Classification à classes multiples
• Classification un contre tous
• softmax (classification un contre un)