Diese Seite wurde von der Cloud Translation API übersetzt.

Neuronale Netzwerke: Klassifizierung mehrerer Klassen

Zuvor haben Sie Binärklassifizierung Modelle, die zwischen zwei möglichen Auswahlmöglichkeiten wählen können, z. B.:

Eine bestimmte E-Mail ist Spam oder kein Spam.
Ein bestimmter Tumor ist bösartig oder gutartig.

In diesem Abschnitt untersuchen wir Klassifizierung mit mehreren Klassen Modelle, die aus mehreren Möglichkeiten wählen können. Beispiel:

Ist das ein Beagle, Basset Hound oder Bloodhound?
Ist das eine sibirische Schwertlilie, oder Zwerg-Iris?
Ist das eine Boeing 747, Airbus 320, Boeing 777 oder Embraer 190?
Ist das ein Bild von einem Apfel, einem Bären, einem Süßigkeiten, einem Hund oder einem Ei?

Bei einigen realen Problemen mit mehreren Klassen besteht die Auswahl aus Millionen unterschiedlichen Klassen gibt. Stellen Sie sich z. B. eine Klassifizierung mit mehreren Klassen vor, das Bild von nahezu allem identifizieren kann.

In diesem Abschnitt werden die beiden Hauptvarianten der mehrklassigen Klassifizierung beschrieben:

one-vs.-all
one-vs.-one, auch bekannt als Softmax

1 oder alle

One-vs.-all bietet die Möglichkeit, die binäre Klassifizierung zu verwenden. für eine Reihe von Ja- oder Nein-Vorhersagen über mehrere mögliche Labels hinweg.

Bei einem Klassifizierungsproblem mit n möglichen Lösungen -Lösung besteht aus n separaten binären Klassifikatoren – einem binären Klassifikator für jedes mögliche Ergebnis. Während des Trainings wird das Modell eine Reihe von binären Klassifikatoren, die jeweils so trainiert werden, Klassifizierungsfrage.

Bei einem Bild von einer Frucht können verschiedene Erkennungsmechanismen trainiert werden, die jeweils ein anderes Ja/Nein beantworten. Frage:

Ist dieses Bild ein Apfel?
Ist dieses Bild orange?
Ist dieses Bild eine Banane?
Ist dieses Bild eine Traube?

Die folgende Abbildung zeigt, wie das in der Praxis funktioniert.

Abbildung 7. Ein Bild einer Birne, das als Eingabe an vier verschiedene
binären Klassifikatoren. Das erste Modell sagt „Apfel“ vorher oder 'nicht
Apfel' und die Vorhersage ist 'not apple'. Das zweite Modell sagt
"orange" oder "not orange" und die Vorhersage ist "not orange". Die
drittes Modell sagt „Birne“ vorher. oder "not pear". Die Vorhersage lautet
'Birne'. Das vierte Modell sagt „Traube“ vorher. oder 'not trabe' [not trabe] und
Vorhersage ist „not grape“. — </ph> Abbildung 7: Ein Bild einer Birne, das als Eingabe an vier verschiedene binären Klassifikatoren. Das erste, zweite und vierte Modell (Vorhersage ob auf dem Bild ein Apfel, eine Orange oder eine Traube zu sehen ist) die negative Klasse vorhersagen. Das dritte Modell (Vorhersagen, ob Das Bild ist eine Birne) sagt die positive Klasse vorher.

Dieser Ansatz ist ziemlich vernünftig, wenn die Gesamtzahl der Klassen ist klein, wird aber mit zunehmender Anzahl von Klassen zunehmend ineffizienter. steigt.

Wir können ein wesentlich effizienteres Modell mit einem neuronalen Deep-Learning-Netzwerk, in dem jeder Ausgabeknoten einen anderen . Die folgende Abbildung veranschaulicht diesen Ansatz.

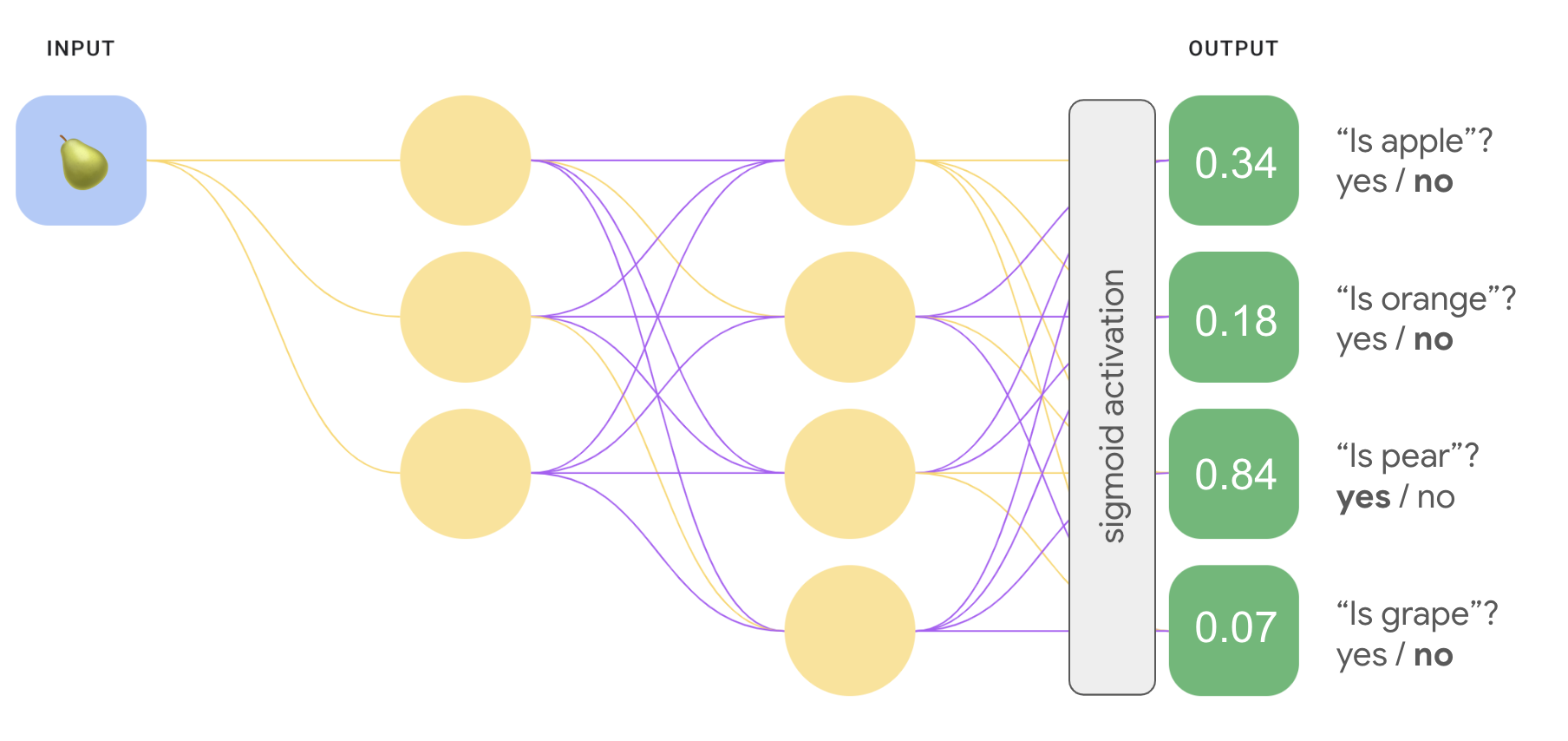Abbildung 8. Ein neuronales Netzwerk mit folgender Architektur: Eingabeschicht mit
1 Knoten, verborgene Ebene mit 3 Knoten, verborgene Ebene mit 4 Knoten
Ausgabeebene mit 4 Knoten. Der Eingabeknoten wird mit dem Bild einer Birne gespeist.
Auf die Ausgabeebene wird eine Sigmoid-Aktivierungsfunktion angewendet. Jedes
Ausgabeknoten stellt die Wahrscheinlichkeit dar, mit der das Bild spezifiziert ist
Früchte. Ausgabeknoten 1 steht für „Is apple?“ (Ist Apfel?) und den Wert 0,34 hat.
Ausgabeknoten 2 steht für „Ist orange?“. und hat den Wert 0,18.
Ausgabeknoten 3 steht für „Is pear?“. und den Wert 0,84 hat.
Ausgabeknoten 4 steht für „Is grape?“ (Ist Traube?) und den Wert 0,07 hat. — </ph> Abbildung 8: Dieselben Klassifizierungsaufgaben wie „1 vs. alle“, die mithilfe eines eines neuronalen Netzes. Eine Sigmoid-Aktivierungsfunktion wird auf die Ausgabe angewendet Jeder Ausgabewert stellt die Wahrscheinlichkeit dar, dass die Eingabe eine bestimmte Frucht ist. Dieses Modell sagt voraus, dass 84% die Wahrscheinlichkeit, dass das Bild eine Birne ist, und eine Wahrscheinlichkeit von 7 %, dass das Bild eine Birne ist Traube.

1 vs. 1 (Softmax)

Sie haben vielleicht bemerkt, dass die Wahrscheinlichkeitswerte in der Ausgabeebene in Abbildung 8 nicht 1,0 oder 100 % ergeben. Tatsächlich ergeben sie insgesamt 1, 43. In einer Eins-gegen-alle- wird die Wahrscheinlichkeit jedes binären Ergebnissatzes bestimmt, unabhängig von allen anderen Sets. Das heißt, wir ermitteln die Wahrscheinlichkeit, von "Apfel" im Vergleich zu "not apple" ohne die Wahrscheinlichkeit zu berücksichtigen, Obstoptionen: „Orange“, „Birne“ oder „Traube“.

Aber was ist, wenn wir die Wahrscheinlichkeit für jede Früchte vorhersagen möchten, relativ zueinander? Anstatt „Apfel“ vorherzusagen, im Vergleich zu „nicht Apfel“ wollen wir „Apfel“ vorhersagen im Vergleich zu "Orange" im Vergleich zu "Birne" im Vergleich zu "Traube". Diese Art der Klassifizierung mehrerer Klassen wird als Klassifizierung mit einer oder nicht von einer bezeichnet.

Wir können eine 1-gegen-1-Klassifizierung mit demselben neuronalen Netzwerkarchitektur für die Klassifizierung im Vergleich zu allen anderen mit einer Schlüsseländerung Wir müssen eine andere Transformation auf die Ausgabeebene anwenden.

Für „1-vs.-all“ haben wir die Sigmoid-Aktivierungsfunktion auf jede Ausgabe angewendet. Knoten unabhängig. Dies führte zu einem Ausgabewert zwischen 0 und 1 für jeden Knoten definiert, aber nicht garantiert, dass diese Summe genau 1 ergibt.

Für Eins gegen Eins können wir stattdessen die Funktion Softmax anwenden, die weist jeder Klasse in einem mehrklassigen Problem dezimale Wahrscheinlichkeiten zu, sodass addieren alle Wahrscheinlichkeiten 1,0. Diese zusätzliche Einschränkung dass das Training schneller konvergiert, als es sonst der Fall wäre.

Klicken Sie auf das Plus-Symbol, um die Softmax-Gleichung anzuzeigen.

Die Softmax-Gleichung lautet wie folgt:

$$p(y = j|\textbf{x}) = \frac{e^{(\textbf{w}_j^{T}\textbf{x} + b_j)}}{\sum_{k\in K} {e^{(\textbf{w}_k^{T}\textbf{x} + b_k)}} }$$

Beachten Sie, dass diese Formel im Grunde die Formel für logistische in mehrere Klassen unterteilen.

In der folgenden Abbildung wird unsere „1-vs.-all“-Klassifizierung mit mehreren Klassen neu implementiert. 1-gegen-1-Aufgabe lösen können. Um Softmax auszuführen, muss das ausgeblendete die direkt vor dem Ausgabe-Layer (sogenannter Softmax-Layer) die gleiche Anzahl von Knoten wie die Ausgabeschicht.

Abbildung 9. Ein neuronales Netzwerk mit folgender Architektur: Eingabe
Schicht mit 1 Knoten, versteckte Schicht mit 3 Knoten, versteckte Schicht mit 4 Knoten
Ausgabeebene mit 4 Knoten. Der Eingabeknoten wird mit dem Bild einer Birne gespeist.
Eine Softmax-Aktivierungsfunktion wird auf die Ausgabeebene angewendet. Jedes
Ausgabeknoten stellt die Wahrscheinlichkeit dar, mit der das Bild spezifiziert ist
Früchte. Ausgabeknoten 1 steht für „Is apple?“ (Ist Apfel?) und hat den Wert 0,19.
Ausgabeknoten 2 steht für „Ist orange?“. und den Wert 0,12 hat.
Ausgabeknoten 3 steht für „Is pear?“. und den Wert 0,63 hat.
Ausgabeknoten 4 steht für „Is grape?“ (Ist Traube?) und den Wert 0,06 hat. — </ph> Abbildung 9: Implementierung eines neuronalen Netzes einer 1-gegen-1-Klassifizierung unter Verwendung von Softmax-Layer. Jeder Ausgabewert steht für die Wahrscheinlichkeit, Eingabebild ist die angegebene Frucht und keine der anderen drei Früchte. (Summe aller Wahrscheinlichkeiten 1,0). Dieses Modell sagt voraus, dass 63% Wahrscheinlichkeit, dass das Bild eine Birne ist.

Softmax-Optionen

Sehen Sie sich die folgenden Softmax-Varianten an:

Full Softmax ist der Softmax-Messwert, über den wir bereits gesprochen haben. also: Softmax berechnet eine Wahrscheinlichkeit für jede mögliche Klasse.
Kandidat für Stichproben bedeutet, dass Softmax eine Wahrscheinlichkeit berechnet. für alle positiven Labels, aber nur für eine Zufallsstichprobe von negative Labels. Wenn wir z. B. daran interessiert sind, ob das Eingabebild ein Beagle oder ein Bloodhound ist, stellen Wahrscheinlichkeiten für jedes Beispiel bereit, das kein Hund ist.

Full Softmax ist relativ günstig, wenn die Anzahl der Klassen gering ist. wird aber mit steigender Anzahl der Klassen ungeheuer teuer. Die Auswahl der Kandidaten kann bei Problemen mit einer großen Anzahl der Klassen.

Ein Label im Vergleich zu vielen Labels

Softmax geht davon aus, dass jedes Beispiel zu genau einer Klasse gehört. Einige Beispiele können jedoch gleichzeitig Mitglied mehrerer Klassen sein. Beispiele:

Sie dürfen Softmax nicht verwenden.
Sie müssen sich auf mehrere logistische Regressionen verlassen.

Das 1-gegen-1-Modell in Abbildung 9 oben geht beispielsweise davon aus, genau eine Obstsorte darstellt: einen Apfel, eine Orange, eine Birne oder Traube. Wenn ein Eingabebild jedoch mehrere Obstsorten enthalten könnte – ein Schüssel mit Äpfeln und Orangen haben, müssen Sie mehrere logistische Regressionen behandelt.

Zurück

Interaktive Übungen (15 min)

Weiter

Testen Sie Ihr Wissen (10 Min.)