Neuronale Netzwerke

Vielleicht erinnern Sie sich aus dem Funktionsübergreifende Übungen im Modul Kategoriale Daten dass das folgende Klassifizierungsproblem nicht linear ist:

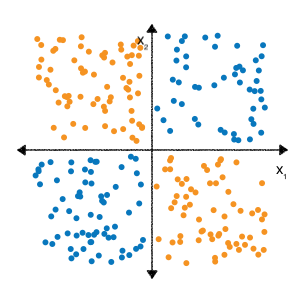
Abbildung 1: kartesische Koordinatenebene, unterteilt in vier Quadranten, die alle mit zufälligen Punkten gefüllt sind, die einer Form ähneln, . Die Punkte oben rechts und links unten sind blau, und die Punkte oben links und unten rechts sind orange.
Abbildung 1. Nicht lineares Klassifizierungsproblem. Eine lineare Funktion kann die blauen von den orangefarbenen Punkten.

„Nicht linear“ bedeutet, dass Sie ein Label mit einem der Form \(b + w_1x_1 + w_2x_2\). Mit anderen Worten, der Parameter „Entscheidungsfläche“ ist keine Linie.

Wenn wir jedoch eine Funktionsverknüpfung für die Funktionen $x_1$ und $x_2$ durchführen, stellen dann die nicht lineare Beziehung zwischen den beiden Funktionen mithilfe eines lineares Modell: $b + w_1x_1 + w_2x_2 + w_3x_3$, wobei $x_3$ die Merkmalsverknüpfung zwischen $x_1$ und $x_2$:

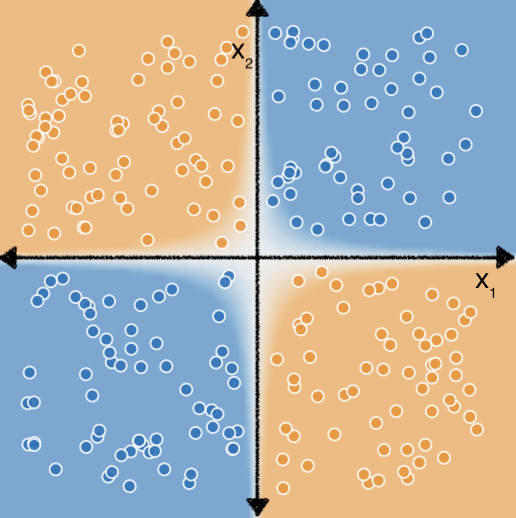
Abbildung 2. Die gleiche kartesische Koordinatenebene von Blau und Orange wie in Abbildung 1 dargestellt. Diesmal ist jedoch eine weiße hyperbolische Kurve über dem Raster, wodurch die blauen Punkte oben rechts und die Quadranten unten links (jetzt mit blauem Hintergrund) von der die orangefarbenen Punkte oben links und rechts unten (jetzt orangefarbenen Hintergrund).
Abbildung 2. Durch das Hinzufügen der Funktionsverknüpfung x1x2 kann das lineare Modell lernen, eine hyperbolische Form, die die blauen von den orangefarbenen Punkten trennt.

Betrachten Sie nun das folgende Dataset:

Abbildung 3: kartesische Koordinatenebene, unterteilt in vier Quadranten. Ein kreisförmiger Cluster mit blauen Punkten ist am Ursprung des und wird von einem Ring aus orangefarbenen Punkten umgeben. <ph type="x-smartling-placeholder">
</ph> Abbildung 3: Ein schwierigeres nicht lineares Klassifizierungsproblem.

Vielleicht erinnern Sie sich auch aus den Übungsreihen zu Funktionsverknüpfungen. dass die Bestimmung des richtigen Merkmals sich überschneidet, um ein lineares Modell an diese Daten anzupassen. etwas mehr Aufwand und Experimentierfreude.

Aber was wäre, wenn Sie nicht all die Experimente selbst durchführen müssten? neuronale Netzwerke gehören zu einer Familie von Modellarchitekturen, die darauf ausgelegt sind, nicht linear Muster in Daten. Beim Training eines neuronalen Netzwerks model automatisch lernt die optimalen Funktionsverknüpfungen für die Eingabedaten, um Verlust.

In den folgenden Abschnitten erfahren Sie, wie neuronale Netzwerke funktionieren.

Zurück
Testen Sie Ihr Wissen (10 Min.)
Weiter
Knoten und ausgeblendete Ebenen (15 Min.)