Sieci neuronowe

Jak być może pamiętasz, Funkcje ćwiczeń przekrojowych w module Dane kategorialne, że następujący problem klasyfikacji jest nieliniowy:

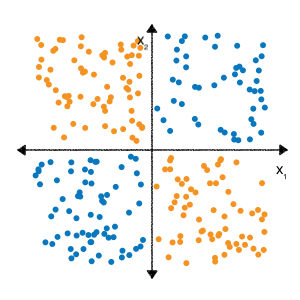
Rysunek 1. Kartezyjski układ współrzędnych podzielony na cztery ćwiartki, z których każdy jest wypełniony losowymi kropkami, do kwadratu. Kropki w prawym górnym i lewym dolnym rogu są niebieskie, a kropki w lewym górnym i prawym dolnym rogu są pomarańczowe.
Rysunek 1. Problem z klasyfikacją nieliniową. Funkcja liniowa nie może wyraźnie oddzielić wszystkie niebieskie kropki od pomarańczowych.

„Nielinearne” oznacza, że nie można dokładnie przewidzieć etykiety z ma postać \(b + w_1x_1 + w_2x_2\). Innymi słowy, "obszar decyzyjny" nie jest linią.

Jeśli jednak przeprowadzimy przekrój cech $x_1$ i $x_2$, możemy następnie zdefiniuj zależność nieliniową między dwoma obiektami za pomocą model liniowy: $b + w_1x_1 + w_2x_2 + w_3x_3$, gdzie $x_3$ to przecięcie funkcji $x_1$ i $x_2$:

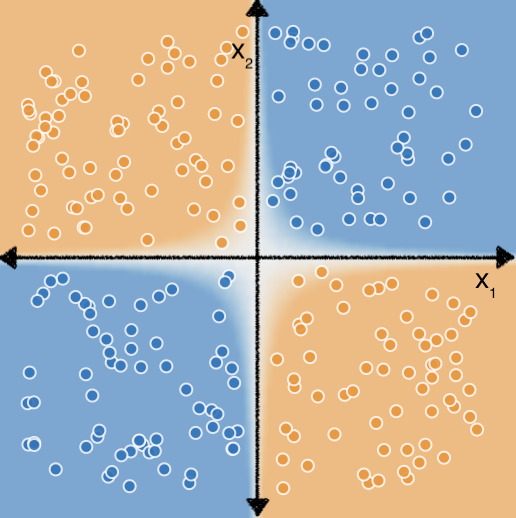
Rysunek 2. Ta sama kartezjańska płaszczyzna współrzędnych niebieskiego i pomarańczowego jak na rys. 1. Tym razem jednak biała krzywa hiperboliczna są wyświetlane nad siatką, która rozdziela niebieskie punkty w prawym górnym rogu, i lewe dolne ćwiartki (teraz zacienione na niebieskim tle) od pomarańczowe kropki w lewym górnym i prawym dolnym rogu (teraz z pomarańczowym tłem).
Rysunek 2. Przez dodanie krzyżyków x1x2, model liniowy może się uczyć hiperboliczny kształt oddzielający niebieskie kropki od pomarańczowych.

Teraz przyjrzyjmy się temu zbiorowi danych:

Rysunek 3. Kartezyjski układ współrzędnych, podzielony na cztery ćwiartki. Okrągły zbiór niebieskich kropek jest wyśrodkowany na początku i jest otoczony pierścieniem pomarańczowych kropek.
Rysunek 3. Trudny problem z klasyfikacją nieliniową.

Być może warto też zapamiętać z ćwiczeń łączących cechy. aby określenie właściwych cech przecinały się, aby dopasować model liniowy do tych danych wymagało to więcej wysiłku i eksperymentów.

Ale co by było, gdyby nie trzeba było samodzielnie przeprowadzać eksperymentów? Sieci neuronowe to rodzina architektur modeli zaprojektowanych pod kątem znajdowania nieliniowe w danych. Podczas trenowania sieci neuronowej model automatycznie uczy się optymalne krzyżówki cech, które będą działać na danych wejściowych, aby zminimalizować straty.

W kolejnych sekcjach przyjrzymy się bliżej, jak działają sieci neuronowe.

Wstecz
Sprawdź swoją wiedzę (10 min)
Dalej
Węzły i ukryte warstwy (15 min)