Нейронні мережі

Ви можете пригадати з вправ на поєднання ознак, наведених у модулі "Категорійні дані", що ця задача класифікації нелінійна:

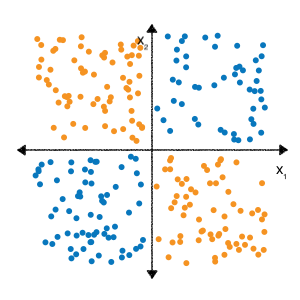
Рисунок 1. Декартова координатна площина, розділена на чотири квадранти, кожен із яких заповнено випадковими точками, що за формою нагадують квадрат. Точки у верхньому правому й нижньому лівому квадрантах – сині, а у верхньому лівому й нижньому правому – помаранчеві.
Рисунок 1. Нелінійна задача класифікації. Лінійна функція не може чітко відокремити всі сині точки від помаранчевих.

"Нелінійна" означає, що не можна точно спрогнозувати мітку за допомогою моделі у вигляді \(b + w_1x_1 + w_2x_2\). Іншими словами, "поверхня рішень" – це не лінія.

Однак, якщо поєднати ознаки $x_1$ і $x_2$, між ними буде встановлено нелінійний зв’язок за допомогою лінійної моделі: $b + w_1x_1 + w_2x_2 + w_3x_3$, де $x_3$ – поєднання ознак $x_1$ і $x_2$:

Рисунок 2. Та сама декартова координатна площина із синіми й помаранчевими точками, що й на рисунку 1. Однак цього разу поверх сітки нанесено білу гіперболічну криву, яка відокремлює сині точки, розміщені в правому верхньому й лівому нижньому квадрантах (тепер на синьому фоні) від помаранчевих точок, наявних у лівому верхньому й правому нижньому квадрантах (тепер на помаранчевому фоні).
Рисунок 2. Якщо додати поєднання ознак x1x2, лінійна модель може вивчити гіперболічну форму, яка відокремлює сині точки від помаранчевих.

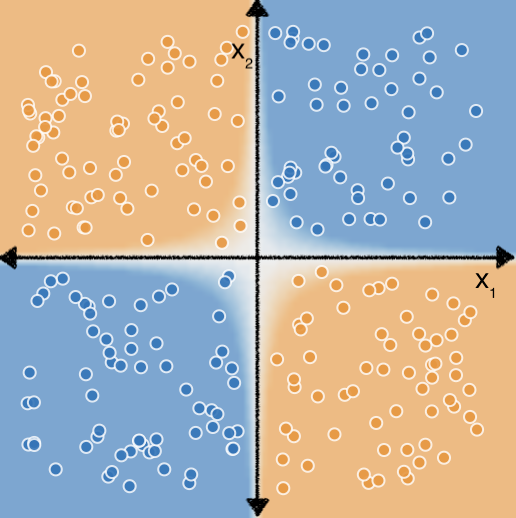
Тепер розгляньмо такий набір даних:

Рисунок 3. Декартова координатна площина, розділена на чотири квадранти. Кругове скупчення синіх точок відцентровано відносно початку координат і оточено кільцем помаранчевих точок.
Рисунок 3. Складніша нелінійна задача класифікації.

Ви можете також пам’ятати з вправ на поєднання ознак, що потрібно докласти більше зусиль і поекспериментувати, щоб визначити правильні поєднання для пристосування лінійної моделі до таких даних.

А що як вам не доведеться проводити всі ці експерименти самостійно? Нейронні мережі – це сімейство архітектур моделей, призначених для пошуку нелінійних закономірностей у даних. Під час тренування нейронної мережі модель автоматично вивчає, які поєднання ознак будуть оптимальними для вхідних даних і мінімізують втрати.

У наступних розділах ми докладно розглянемо, як працюють нейронні мережі.

Назад
知识测验（10 分钟）
Далі
节点和隐藏层（15 分钟）