איור 1. בעיית סיווג לא ליניארית. פונקציה לינארית לא יכולה להפריד בבירור בין כל הנקודות הכחולות לנקודות הכתומות.
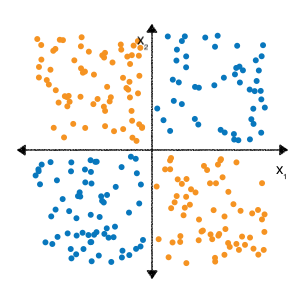
'לא לינארי' פירושו שלא ניתן לחזות באופן מדויק תווית עם
בצורת \(b + w_1x_1 + w_2x_2\). במילים אחרות,
'שטח לקבלת החלטה' הוא לא שורה.
עם זאת, אם נבצע שילוב של תכונות בתכונות $x_1$ ו-$x_2$, נוכל
שמייצג את הקשר הלא ליניארי בין שתי התכונות באמצעות
מודל לינארי:
$b + w_1x_1 + w_2x_2 + w_3x_3$ כאשר $x_3$ הוא שילוב התכונות
$x_1$ ו-$x_2$:
איור 2. הוספת המכפלה של המאפיינים x1x2 מאפשרת למודל ליניארי ללמוד צורה היפרבולית שמפרידה בין הנקודות הכחולות לנקודות הכתומות.
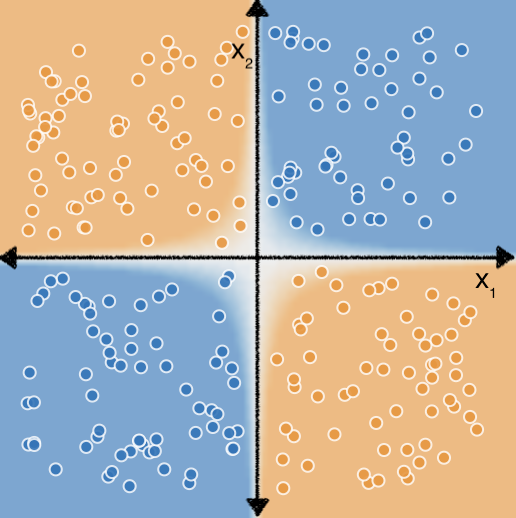
עכשיו נבחן את מערך הנתונים הבא:
איור 3. בעיית סיווג לא ליניארית קשה יותר.
אפשר גם להיזכר בתרגילי פיצ'ר
שקובעת מהי התכונה הנכונה חוצה כדי להתאים מודל ליניארי לנתונים האלה
השקענו קצת יותר מאמץ וניסויים.
אבל מה אם לא הייתם צריכים לבצע את כל הניסויים האלה בעצמכם?
רשתות נוירונים הן משפחה של ארכיטקטורות מודל שנועדו לזהות דפוסים לא לינאריים בנתונים. במהלך האימון של רשת נוירונים,
בניית מודל באופן אוטומטי
לומדת את הצלבות התכונות האופטימליות שצריך לבצע על נתוני הקלט כדי לצמצם
.
בחלקים הבאים נבחן לעומק את אופן הפעולה של רשתות נוירונים.
[null,null,["עדכון אחרון: 2025-07-27 (שעון UTC)."],[[["\u003cp\u003eThis module explores neural networks, a model architecture designed to automatically identify nonlinear patterns in data, eliminating the need for manual feature cross experimentation.\u003c/p\u003e\n"],["\u003cp\u003eYou will learn the fundamental components of a deep neural network, including nodes, hidden layers, and activation functions, and how they contribute to prediction.\u003c/p\u003e\n"],["\u003cp\u003eThe module covers the training process of neural networks, using the backpropagation algorithm to optimize predictions and minimize loss.\u003c/p\u003e\n"],["\u003cp\u003eAdditionally, you will gain insights into how neural networks handle multi-class classification problems using one-vs.-all and one-vs.-one approaches.\u003c/p\u003e\n"],["\u003cp\u003eThis module builds on prior knowledge of machine learning concepts such as linear and logistic regression, classification, and working with numerical and categorical data.\u003c/p\u003e\n"]]],[],null,["# Neural networks\n\n| **Estimated module length:** 75 minutes\n| **Learning objectives**\n|\n| - Explain the motivation for building neural networks, and the use cases they address.\n| - Define and explain the function of the key components of a deep neural network architecture:\n| - **[Nodes](/machine-learning/glossary#node-neural-network)**\n| - **[Hidden layers](/machine-learning/glossary#hidden_layer)**\n| - **[Activation functions](/machine-learning/glossary#activation_function)**\n| - Develop intuition around how neural network predictions are made, by stepping through the inference process.\n| - Build a high-level intuition of how neural networks are trained, using the backpropagation algorithm.\n| - Explain how neural networks can be used to perform two types of multi-class classification: one-vs.-all and one-vs.-one.\n| **Prerequisites:**\n|\n| This module assumes you are familiar with the concepts covered in the\n| following modules:\n|\n| - [Introduction to Machine Learning](/machine-learning/intro-to-ml)\n| - [Linear regression](/machine-learning/crash-course/linear-regression)\n| - [Logistic regression](/machine-learning/crash-course/logistic-regression)\n| - [Classification](/machine-learning/crash-course/classification)\n| - [Working with numerical data](/machine-learning/crash-course/numerical-data)\n| - [Working with categorical data](/machine-learning/crash-course/categorical-data)\n| - [Datasets, generalization, and overfitting](/machine-learning/crash-course/overfitting)\n\nYou may recall from the\n[Feature cross exercises](/machine-learning/crash-course/categorical-data/feature-cross-exercises)\nin the [Categorical data module](/machine-learning/crash-course/categorical-data),\nthat the following classification problem is nonlinear:\n**Figure 1.** Nonlinear classification problem. A linear function cannot cleanly separate all the blue dots from the orange dots.\n\n\"Nonlinear\" means that you can't accurately predict a label with a\nmodel of the form \\\\(b + w_1x_1 + w_2x_2\\\\). In other words, the\n\"decision surface\" is not a line.\n\nHowever, if we perform a feature cross on our features $x_1$ and $x_2$, we can\nthen represent the nonlinear relationship between the two features using a\n[**linear model**](/machine-learning/glossary#linear-model):\n$b + w_1x_1 + w_2x_2 + w_3x_3$ where $x_3$ is the feature cross between\n$x_1$ and $x_2$:\n**Figure 2.** By adding the feature cross *x* ~1~*x* ~2~, the linear model can learn a hyperbolic shape that separates the blue dots from the orange dots.\n\nNow consider the following dataset:\n**Figure 3.** A more difficult nonlinear classification problem.\n\nYou may also recall from the [Feature cross exercises](/machine-learning/crash-course/categorical-data/feature-cross-exercises)\nthat determining the correct feature crosses to fit a linear model to this data\ntook a bit more effort and experimentation.\n\nBut what if you didn't have to do all that experimentation yourself?\n[**Neural networks**](/machine-learning/glossary#neural_network) are a family\nof model architectures designed to find\n[**nonlinear**](/machine-learning/glossary#nonlinear)\npatterns in data. During training of a neural network, the\n[**model**](/machine-learning/glossary#model) automatically\nlearns the optimal feature crosses to perform on the input data to minimize\nloss.\n\nIn the following sections, we'll take a closer look at how neural networks work.\n| **Key terms:**\n|\n| - [Activation function](/machine-learning/glossary#activation_function)\n| - [Hidden layer](/machine-learning/glossary#hidden_layer)\n| - [Linear model](/machine-learning/glossary#linear-model)\n| - [Model](/machine-learning/glossary#model)\n| - [Neural network](/machine-learning/glossary#neural_network)\n| - [Nodes](/machine-learning/glossary#node-neural-network)\n- [Nonlinear](/machine-learning/glossary#nonlinear) \n[Help Center](https://support.google.com/machinelearningeducation)"]]
