前述したように、 特徴クロスの演習 カテゴリデータ モジュールでは、 次の分類問題が非線形であることがわかります。
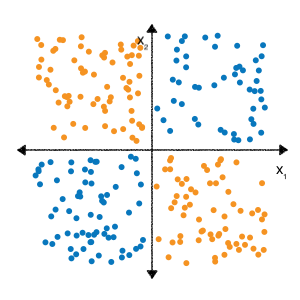
「非線形」とは、 \(b + w_1x_1 + w_2x_2\)形式のモデルではラベルを正確に予測できないことを意味します。つまり、「決定サーフェス」は線ではありません。
ただし、特徴量 $x_1$ と $x_2$ で特徴量の交差を実行すると、線形モデル $b + w_1x_1 + w_2x_2 + w_3x_3$ を使用して、2 つの特徴量間の非線形関係を表すことができます。ここで、$x_3$ は $x_1$ と $x_2$ の特徴量の交差です。
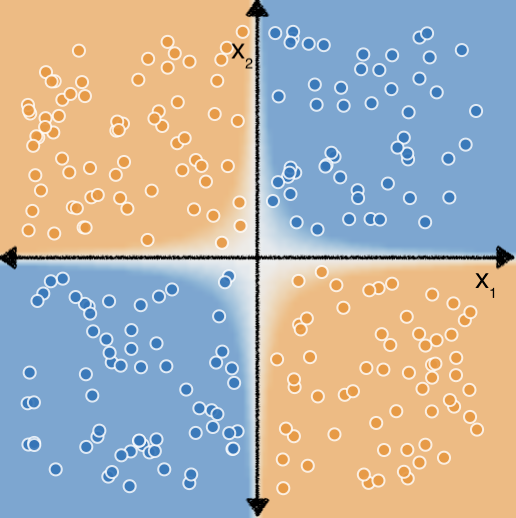
次のデータセットについて考えてみましょう。

特徴の交差演習でも説明しましたが、このデータに線形モデルを適合させる正しい特徴の交差を決定するには、もう少しの労力とテストが必要でした。
しかし、そのようなテストをすべて自分で行う必要がないとしたらどうでしょうか。 ニューラル ネットワークは、 モデルアーキテクチャの nonlinear パターンです。ニューラル ネットワークのトレーニング中に、モデルは、損失を最小限に抑えるために入力データに対して実行する最適な特徴量の交差を自動的に学習します。
以降のセクションでは、ニューラル ネットワークの仕組みについて詳しく説明します。
