การเชื่อมโยง (เรียกอีกอย่างว่า bucketing) คือ
Feature Engineering
เทคนิคที่จัดกลุ่มช่วงย่อยของตัวเลขต่างๆ เป็น bin หรือ
ที่เก็บข้อมูล
ในหลายกรณี Binning จะเปลี่ยนข้อมูลตัวเลขให้เป็นข้อมูลเชิงหมวดหมู่
เช่น ลองพิจารณาฟีเจอร์
ชื่อ X ซึ่งมีค่าต่ำสุดคือ 15 และ
ค่าสูงสุดคือ 425 เมื่อใช้ Binning คุณสามารถเป็นตัวแทนของ X ด้วยฟังก์ชัน
5 ถังขยะดังต่อไปนี้
- ถัง 1: 15 ถึง 34
- ถัง 2: 35 ถึง 117
- ถัง 3: 118 ถึง 279
- ถัง 4: 280 ถึง 392
- ถัง 5: 393 ถึง 425
ถังขยะ 1 จะครอบคลุมช่วง 15 ถึง 34 ดังนั้นทุกค่าของ X จะอยู่ระหว่าง 15 ถึง 34
จะไปอยู่ใน Bin 1 โมเดลที่ฝึกกับ Bin เหล่านี้จะไม่ตอบสนองต่างกัน
เป็น X ที่มีค่า 17 และ 29 เนื่องจากทั้ง 2 ค่าอยู่ใน Bin 1
เวกเตอร์คุณลักษณะ แสดง 5 ถังขยะดังนี้
| หมายเลข Bin | ช่วง | เวกเตอร์ของจุดสนใจ |
|---|---|---|
| 1 | 15-34 | [1.0, 0.0, 0.0, 0.0, 0.0] |
| 2 | 35-117 | [0.0, 1.0, 0.0, 0.0, 0.0] |
| 3 | 118-279 | [0.0, 0.0, 1.0, 0.0, 0.0] |
| 4 | 280-392 | [0.0, 0.0, 0.0, 1.0, 0.0] |
| 5 | 393-425 | [0.0, 0.0, 0.0, 0.0, 1.0] |
แม้ว่า X จะเป็นคอลัมน์เดียวในชุดข้อมูล แต่การเชื่อมโยงจะทําให้โมเดล
เพื่อถือว่า X เป็นคุณลักษณะที่แยกกันห้า ดังนั้น โมเดลจะเรียนรู้
น้ำหนักแยกกันสำหรับแต่ละถัง
Binning เป็นทางเลือกที่ดีในการปรับขนาด หรือการตัดเมื่อ ตรงตามเงื่อนไขต่อไปนี้
- ความสัมพันธ์แบบเชิงเส้นโดยรวมระหว่างฟีเจอร์กับ ป้ายกำกับใช้งานไม่ได้หรือไม่มีอยู่
- เมื่อมีการรวมค่าฟีเจอร์
Binning อาจดูขัดกับสัญชาตญาณเนื่องจากโมเดลใน ตัวอย่างก่อนหน้านี้ถือว่าค่า 37 และ 115 เหมือนกัน แต่เมื่อ มีเนื้อหาที่ดูไม่สมบูรณ์มากกว่าเนื้อหาแบบเชิงเส้น การใช้ Binning เป็นวิธีที่ดีกว่ามาก แสดงถึงข้อมูลนั้นๆ
ตัวอย่างการสรุป: จำนวนผู้เลือกซื้อเทียบกับอุณหภูมิ
สมมติว่าคุณกำลังสร้างโมเดลที่คาดคะเนจำนวนของ ตามอุณหภูมิภายนอกของวันดังกล่าวในวันนั้นๆ นี่คือพล็อตของ อุณหภูมิเทียบกับจำนวนผู้เลือกซื้อ:
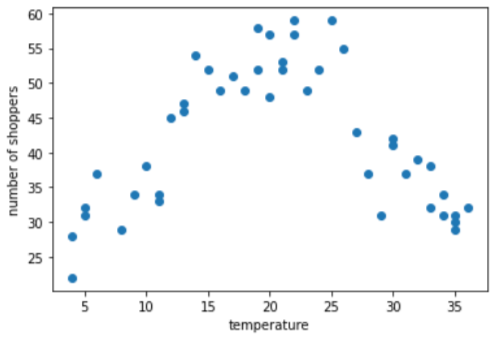
โครงเรื่องได้แสดงให้เห็นว่าจำนวนผู้เลือกซื้อสูงสุดเมื่อ อุณหภูมิตอนนั้นรู้สึกสบายที่สุด
คุณสามารถแสดงจุดสนใจเป็นค่าดิบได้ ซึ่งก็คืออุณหภูมิที่ 35.0 ใน จะเป็น 35.0 ในเวกเตอร์ฟีเจอร์ นั่นเป็นความคิดที่ดีที่สุดแล้วใช่ไหม
ในระหว่างการฝึก โมเดลการถดถอยเชิงเส้นจะเรียนรู้ค่าน้ำหนักเดียวสำหรับแต่ละ ดังนั้น หากอุณหภูมิแสดงเป็นองค์ประกอบเดียว ค่า ที่อุณหภูมิ 35.0 จะมีผลกระทบ 5 เท่า (หรือ 1 ใน 5 ของผลกระทบ ) ในการคาดคะเนเมื่ออุณหภูมิอยู่ที่ 7.0 อย่างไรก็ตาม พล็อตจะไม่ แสดงความสัมพันธ์เชิงเส้นระหว่างป้ายกำกับกับ ของฟีเจอร์
กราฟแนะนำ 3 คลัสเตอร์ในช่วงย่อยต่อไปนี้
- ถัง 1 คือช่วงอุณหภูมิ 4-11
- ถัง 2 คือช่วงอุณหภูมิ 12-26
- ถัง 3 คือช่วงอุณหภูมิ 27-36
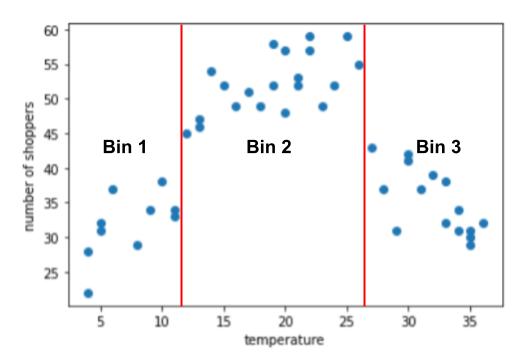
โมเดลจะเรียนรู้น้ำหนักแยกกันสำหรับแต่ละถัง
แม้ว่าคุณจะสามารถสร้างถังขยะมากกว่า 3 ใบ แต่ก็มีถังขยะแยกกันต่างหากสำหรับ ค่าอุณหภูมิที่อ่านได้แต่ละครั้ง มักเป็นความคิดที่ไม่ดีเนื่องจากสาเหตุต่อไปนี้
- โมเดลจะเรียนรู้การเชื่อมโยงระหว่าง Bin และป้ายกำกับเท่านั้นหากมี ตัวอย่างที่เพียงพอใน Bin ในตัวอย่างข้างต้น แต่ละถังทั้ง 3 ใบ มีตัวอย่างอย่างน้อย 10 รายการ ซึ่งอาจเพียงพอสำหรับการฝึก มีถังขยะแยกกัน 33 ใบ ไม่มี Bin ใดที่มีตัวอย่างเพียงพอให้โมเดลฝึกต่อได้
- ดังนั้นการเก็บอุณหภูมิแต่ละก้อนจะแยกออกมาต่างหาก ฟีเจอร์อุณหภูมิแยกกัน 33 แบบ อย่างไรก็ตาม โดยทั่วไปคุณควรลด จำนวนของจุดสนใจในโมเดล
แบบฝึกหัด: ตรวจสอบความเข้าใจ
พล็อตต่อไปนี้แสดงค่ามัธยฐานของราคาบ้านสำหรับแต่ละ 0.2 องศาของ ละติจูดของประเทศฟรีโดเนียตามตำนาน:
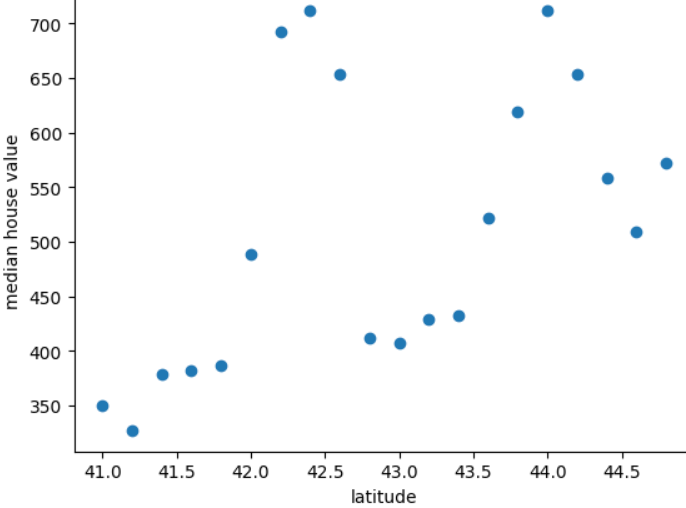
กราฟิกแสดงรูปแบบที่ไม่ใช่เชิงเส้นระหว่างค่าหน้าแรกกับละติจูด ดังนั้นการแสดงละติจูดเป็นค่าจุดลอยตัวก็ไม่น่าจะช่วยอะไรได้ โมเดลสามารถคาดการณ์ได้ดี บางทีการฝากข้อมูลละติจูดอาจดีกว่า ไอเดียของคุณ
- 41.0 ถึง 41.8
- 42.0 ถึง 42.6
- 42.8 ถึง 43.4
- 43.6 ถึง 44.8
การฝากข้อมูลเชิงปริมาณ
การฝากข้อมูลเชิงปริมาณจะสร้างขอบเขตการฝากข้อมูลเพื่อให้จำนวน ของตัวอย่างในแต่ละที่เก็บข้อมูล มีค่าเท่ากับหรือเกือบเท่ากัน การฝากข้อมูลเชิงปริมาณ จะซ่อนค่าผิดปกติไว้เป็นส่วนใหญ่
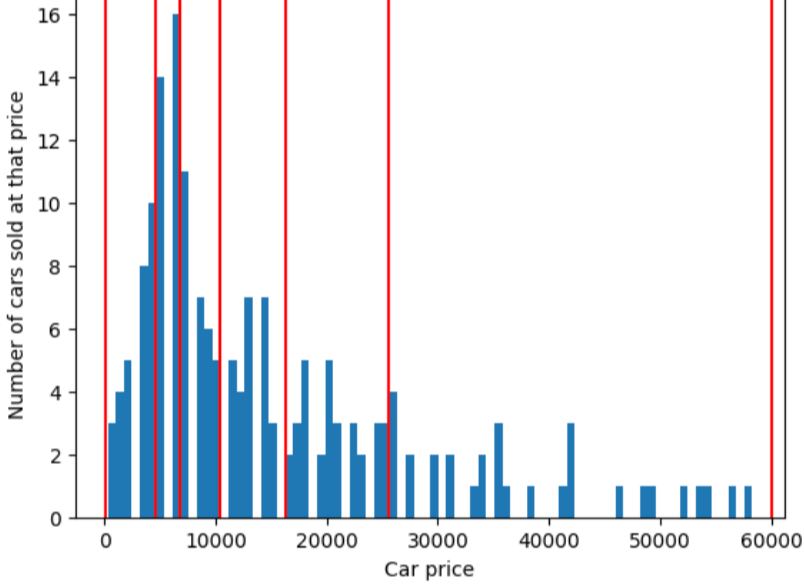
ในการอธิบายปัญหาที่การฝากข้อมูลเชิงควอนไทล์จะแก้ได้ ให้พิจารณา แสดงในรูปต่อไปนี้ โดยที่แต่ละ จากสิบถังหมายถึงจำนวน 10,000 ดอลลาร์พอดี โปรดสังเกตว่าที่เก็บข้อมูลจาก 0 ถึง 10,000 จะมีตัวอย่างหลายสิบรายการ แต่ที่เก็บข้อมูลตั้งแต่ 50,000 ถึง 60,000 จะมีตัวอย่างเพียง 5 รายการ ดังนั้น โมเดลจึงมีตัวอย่างเพียงพอที่จะฝึกในค่า 0 ถึง 10,000 แต่ยังมีตัวอย่างไม่เพียงพอที่จะฝึกสำหรับที่เก็บข้อมูล 50,000 ถึง 60,000 รายการ
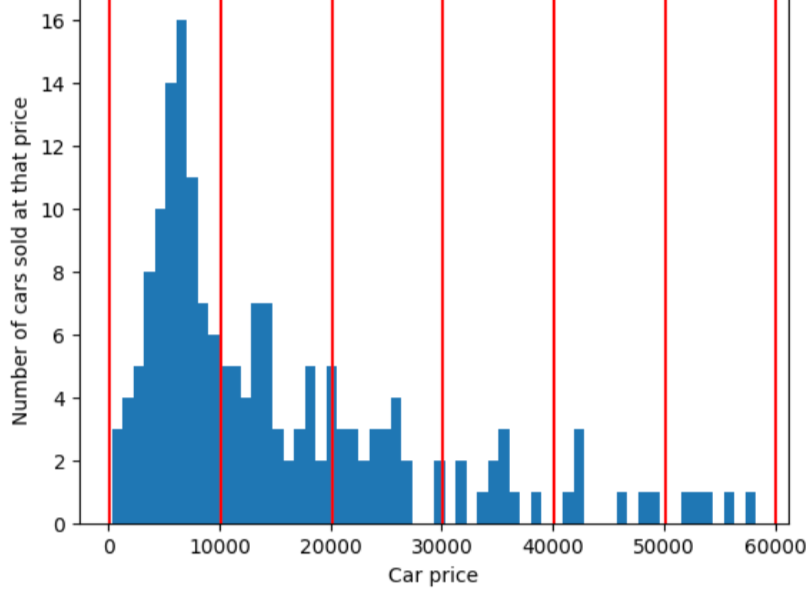
ในทางตรงกันข้าม ตัวเลขต่อไปนี้ใช้การสะสมควอนไทล์เพื่อแบ่งราคารถยนต์ ลงในถังขยะที่มีตัวอย่างจำนวนเท่ากันโดยประมาณในที่เก็บข้อมูลแต่ละชุด สังเกตว่าถังขยะบางกล่องมีช่วงราคาแคบ ขณะที่บางถัง ครอบคลุมช่วงราคาที่กว้างมาก