分箱(也称为分桶)是一种特征工程技术,可将不同的数值子范围分组到箱或桶中。在许多情况下,分箱会将数值数据转换为分类数据。例如,假设有一个名为 X 的特征,其最低值为 15,最高值为 425。使用分箱,您可以使用以下 5 个箱来表示 X:
- 分箱 1:15 至 34
- Bin 2:35 到 117
- Bin 3:118 至 279
- Bin 4:280 至 392
- 箱 5:393 至 425
箱 1 的范围为 15 到 34,因此介于 15 到 34 之间的每个 X 值最终都会进入箱 1。基于这些箱训练的模型对 17 和 29 的 X 值做出的反应不会有任何不同,因为这两个值都位于箱 1 中。
特征向量表示五个箱,如下所示:
| 分箱编号 | Range | 特征向量 |
|---|---|---|
| 1 | 15-34 | [1.0, 0.0, 0.0, 0.0, 0.0] |
| 2 | 35-117 | [0.0, 1.0, 0.0, 0.0, 0.0] |
| 3 | 118-279 | [0.0, 0.0, 1.0, 0.0, 0.0] |
| 4 | 280-392 | [0.0, 0.0, 0.0, 1.0, 0.0] |
| 5 | 393-425 | [0.0, 0.0, 0.0, 0.0, 1.0] |
尽管 X 是数据集中的单列,但分箱会导致模型将 X 视为 5 个单独的特征。因此,模型会为每个箱学习单独的权重。
- 特征与标签之间的总体线性关系较弱或不存在。
- 当特征值聚类时。
鉴于上例中的模型将值 37 和 115 视为相同的值,分箱可能看起来有悖直觉。但如果某个特征的分布比线性分布更集中,那么分箱是表示数据的更好方式。
分箱示例:购物者数量与温度
假设您要创建一个模型,根据当天的室外温度预测购物者人数。下图显示了温度与购物者数量之间的关系:
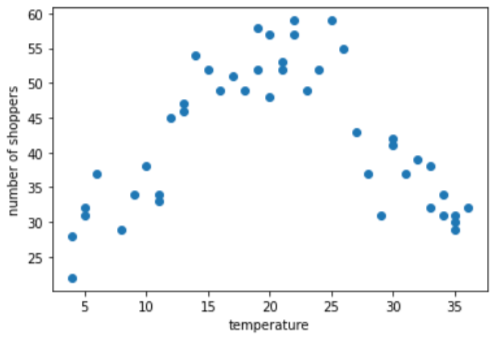
该图显示,毫不意外的是,当温度最舒适时,购物者数量最多。
您可以将特征表示为原始值:数据集中的温度 35.0 在特征向量中将为 35.0。这是最好的主意吗?
在训练期间,线性回归模型会为每个特征学习一个权重。因此,如果温度表示为单个特征,那么 35.0 的温度在预测中的影响力将是 7.0 的温度的五倍(或五分之一)。不过,该图并未真正显示标签与特征值之间的任何线性关系。
该图表显示了以下子范围内的三个聚类:
- 箱 1 是温度范围 4-11。
- 箱 2 是指温度范围 12-26。
- 箱 3 是温度范围 27-36。

模型会为每个箱学习单独的权重。
虽然可以创建三个以上的箱,甚至为每个温度读数创建一个单独的箱,但出于以下原因,这通常不是一个好主意:
- 只有当某个箱中有足够的示例时,模型才能学习箱与标签之间的关联。在给定的示例中,3 个箱中每个箱都包含至少 10 个示例,这可能足以用于训练。如果使用 33 个单独的箱,则没有一个箱会包含足够的样本供模型进行训练。
- 每个温度都使用单独的箱,这样会产生 33 个单独的温度特征。不过,您通常应尽量减少模型中的特征数量。
练习:检查您的理解情况
下图显示了虚构国家弗里多尼亚每 0.2 度纬度的住宅价格中位数:
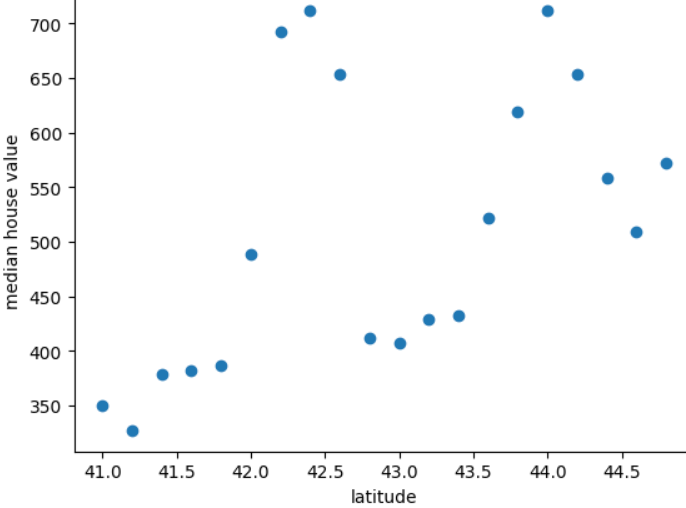
该图显示了房屋价值与纬度之间的非线性关系,因此将纬度表示为浮点值不太可能有助于模型做出良好的预测。或许对纬度进行分桶处理会更好?
- 41.0 至 41.8
- 42.0 至 42.6
- 42.8 至 43.4
- 43.6 至 44.8
分位数分桶
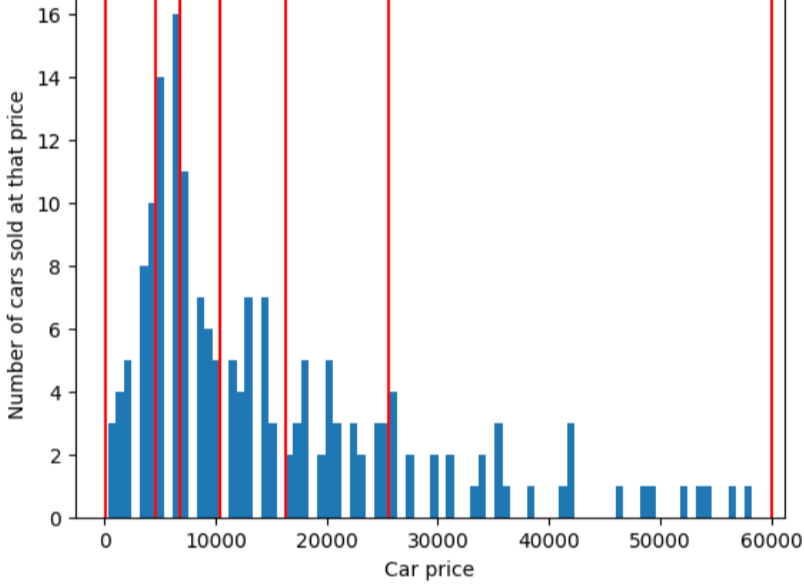
分位数分桶会创建分桶边界,使每个桶中的样本数量完全或几乎相等。分位数分桶主要用于隐藏离群值。
为了说明分位数分桶解决的问题,请考虑下图所示的等间距分桶,其中每个桶代表的范围正好是 10,000 美元。请注意,0 到 10,000 的区间包含数十个示例,而 50,000 到 60,000 的区间仅包含 5 个示例。因此,模型有足够的示例来训练 0 到 10,000 区间,但没有足够的示例来训练 50,000 到 60,000 区间。
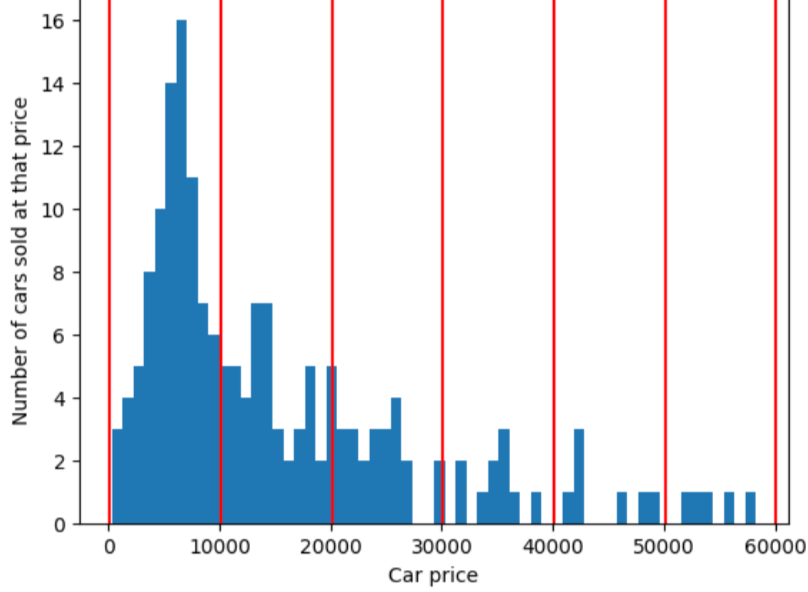
相比之下,下图使用分位数分桶将汽车价格划分为若干个箱,每个箱中包含的样本数量大致相同。请注意,有些箱涵盖的价格范围较窄,而有些箱涵盖的价格范围非常广。