Le binning (également appelé binning) est un
ingénierie des caractéristiques
qui regroupe différentes sous-plages numériques dans des classes ou
buckets :
Dans de nombreux cas, le binning transforme les données numériques en données catégorielles.
Prenons l'exemple d'une fonctionnalité.
nommé X, dont la valeur la plus faible est 15 et
la valeur la plus élevée est 425. À l'aide du binning, vous pouvez représenter X avec le
les cinq classes suivantes:
- Classe 1: 15 à 34
- Classe 2: 35 à 117
- Classe 3: 118 à 279
- Classe 4: 280 à 392
- Classe 5: 393 à 425
Le bin 1 couvre la plage 15 à 34, de sorte que chaque valeur de X est comprise entre 15 et 34
se retrouve dans le bin 1. Un modèle entraîné sur ces classes ne réagira pas différemment
à X des valeurs de 17 et 29, car les deux valeurs se trouvent dans le bin 1.
Le vecteur de caractéristiques représente les cinq bins comme suit:
| Numéro de bin | Plage | Vecteur de caractéristiques |
|---|---|---|
| 1 | 15-34 | [1.0, 0.0, 0.0, 0.0, 0.0] |
| 2 | 35-117 | [0.0, 1.0, 0.0, 0.0, 0.0] |
| 3 | 118-279 | [0,0, 0,0, 1,0, 0,0, 0,0] |
| 4 | 280-392 | [0,0, 0,0, 0,0, 1,0, 0,0] |
| 5 | 393-425 | [0,0, 0,0, 0,0, 0,0, 1,0] |
Même si X est une colonne unique de l'ensemble de données, le binning entraîne le modèle
de traiter X comme cinq caractéristiques distinctes. Par conséquent, le modèle apprend
des pondérations distinctes
pour chaque classe.
Le binning est une bonne alternative au scaling ou le clipping lorsque l'une des les conditions suivantes sont remplies:
- Relation linéaire globale entre la caractéristique et la label est faible ou inexistant.
- Lorsque les valeurs des caractéristiques sont mises en cluster.
Le binning peut sembler contre-intuitif, étant donné que le modèle dans l'exemple précédent traite les valeurs 37 et 115 de manière identique. Mais quand une caractéristique semble plus encombrante que linéaire, le binning est un bien meilleur moyen représentent les données.
Exemple de binning: nombre d'acheteurs par rapport à la température
Supposons que vous créez un modèle qui prédit le nombre clients en fonction de la température extérieure du jour. Voici un graphique des par rapport au nombre d'acheteurs:
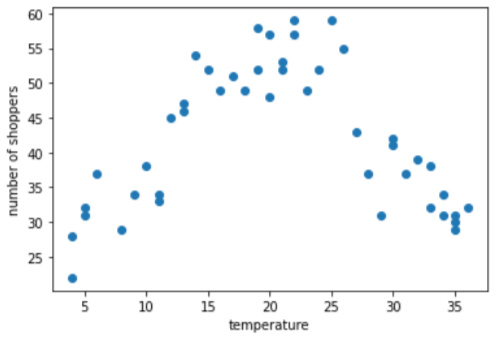
Le tracé montre, sans surprise, que le nombre d'acheteurs était le plus élevé lorsque la température était la plus agréable.
Vous pouvez représenter la caractéristique sous forme de valeurs brutes: une température de 35,0 dans la est de 35,0 dans le vecteur de caractéristiques. Est-ce la meilleure idée ?
Pendant l'entraînement, un modèle de régression linéaire apprend une seule pondération pour chaque . Par conséquent, si la température est représentée par une seule caractéristique, une température de 35,0 aurait cinq fois plus d'influence (ou un cinquième influence) dans une prédiction, sous la forme d'une température de 7,0. Cependant, le tracé ne montrent une relation linéaire entre l'étiquette la valeur de la caractéristique.
Le graphique suggère trois clusters dans les sous-plages suivantes:
- Le bin 1 est la plage de températures 4-11.
- Le bin 2 est la plage de températures 12-26.
- Le bin 3 est la plage de températures de 27 à 36.

Le modèle apprend des pondérations distinctes pour chaque bin.
Bien qu'il soit possible de créer plus de trois bins, même un bin distinct pour chaque température relevée, cette pratique est souvent déconseillée pour les raisons suivantes:
- Un modèle ne peut apprendre l'association entre un bin et une étiquette que s'il existe sont assez d'exemples dans cette classe. Dans l'exemple donné, chacune des trois classes contient au moins 10 exemples, ce qui peut suffire pour l'entraînement. Avec 33 bacs distincts, aucun des bins ne contiendrait suffisamment d'exemples pour l'entraînement du modèle.
- Un bin distinct pour chaque température donne 33 fonctionnalités de température distinctes. Toutefois, vous devez généralement minimiser le nombre de caractéristiques d'un modèle.
Exercice: tester vos connaissances
Le graphique suivant montre le prix médian d’une maison pour chaque 0,2 degré de latitude du pays mythique, la Freedonie:
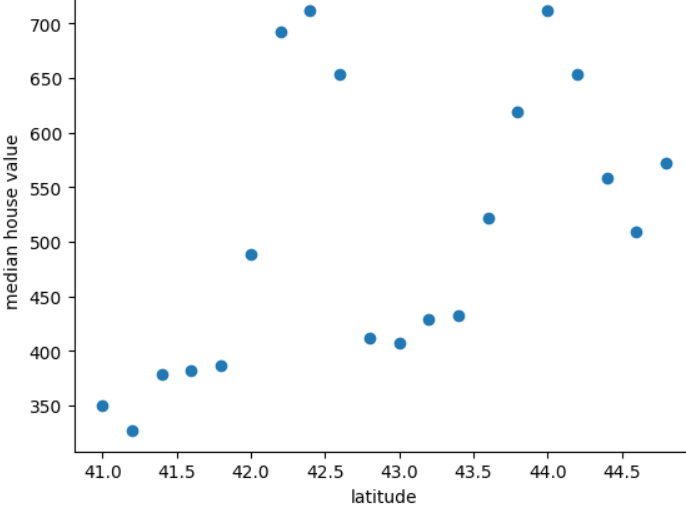
Le graphique montre un schéma non linéaire entre la valeur du logement et la latitude. Il est donc peu probable que représenter la latitude comme sa valeur à virgule flottante pour qu'un modèle réalise de bonnes prédictions. Le binning des latitudes conviendrait peut-être idée ?
- 41,0 à 41,8
- 42,0 à 42,6
- 42,8 à 43,4
- 43,6 à 44,8
Binning de quantiles
Le binning par quantile crée des limites de binning de sorte que le nombre d'exemples dans chaque bucket est exactement ou presque égal. Le binning en quantiles cache principalement les anomalies.
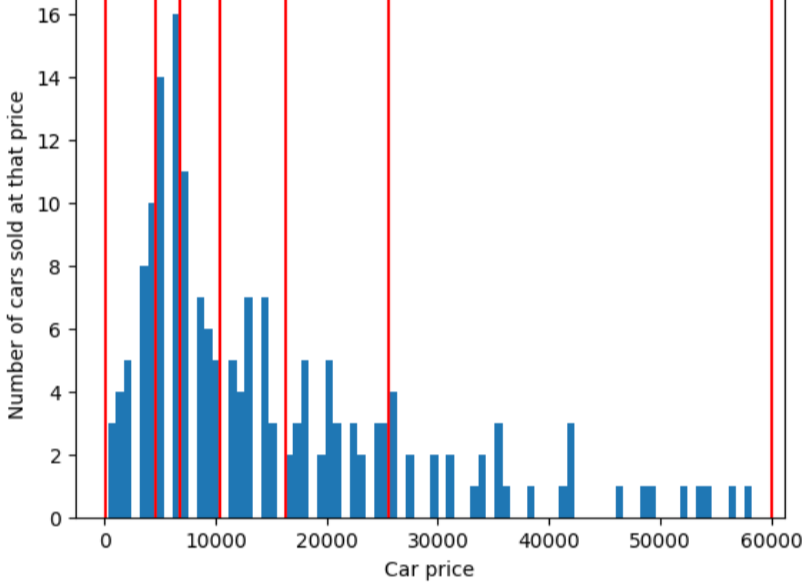
Pour illustrer le problème que permet le binning en quantiles, prenons sont espacés de manière égale, comme illustré dans la figure suivante, où chaque bucket des dix catégories représente une portée de exactement 10 000 dollars. Notez que le bucket compris entre 0 et 10 000 contient des dizaines d'exemples mais le bucket de 50 000 à 60 000 ne contient que 5 exemples. Par conséquent, le modèle dispose de suffisamment d'exemples pour être entraîné sur la plage de 0 à 10 000 mais pas assez d'exemples pour l'entraînement du bucket de 50 000 à 60 000.
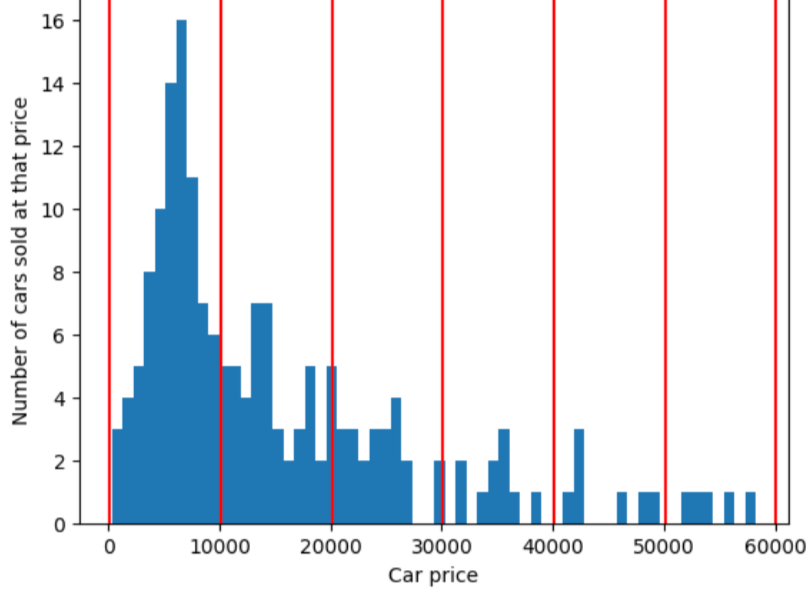
À l'inverse, la figure suivante utilise le binning en quantiles pour diviser le prix des voitures. dans des bins contenant à peu près le même nombre d'exemples dans chaque bucket. Notez que certains segments incluent une fourchette de prix étroite, tandis que d'autres s'adressent à des prix très larges.