Binning (disebut juga bucketing) adalah
rekayasa fitur
teknik yang mengelompokkan subrentang numerik yang berbeda ke dalam kelompok atau
bucket.
Dalam banyak kasus, {i>binning<i} mengubah data numerik menjadi data kategorikal.
Misalnya, pertimbangkan fitur
bernama X yang nilai terendahnya adalah 15 dan
nilai tertinggi adalah 425. Dengan menggunakan binning, Anda dapat merepresentasikan X dengan
lima kelompok berikut:
- Bin 1: 15-34
- Bin 2: 35 hingga 117
- Bin 3: 118-279
- Bin 4: 280 hingga 392
- Bin 5: 393 hingga 425
Bin 1 mencakup rentang 15 hingga 34, sehingga setiap nilai X antara 15 dan 34
berakhir di Bin 1. Model yang dilatih pada kelompok ini tidak akan bereaksi berbeda
menjadi nilai X 17 dan 29 karena kedua nilai berada dalam Bin 1.
Vektor fitur merepresentasikan lima {i>bin<i} sebagai berikut:
| Nomor bin | Rentang | Vektor fitur |
|---|---|---|
| 1 | 15-34 | [1,0, 0,0, 0,0, 0,0, 0,0] |
| 2 | 35-117 | [0,0, 1,0, 0,0, 0,0, 0,0] |
| 3 | 118-279 | [0,0, 0,0, 1,0, 0,0, 0,0] |
| 4 | 280-392 | [0,0, 0,0, 0,0, 1,0, 0,0] |
| 5 | 393-425 | [0,0, 0,0, 0,0, 0,0, 1,0] |
Meskipun X adalah kolom tunggal dalam set data, binning menyebabkan model
untuk memperlakukan X sebagai lima fitur terpisah. Oleh karena itu, model akan mempelajari
bobot terpisah untuk setiap kelompok.
Pengelompokan adalah alternatif yang baik untuk penskalaan atau pemotongan jika salah satu kondisi berikut terpenuhi:
- Keseluruhan hubungan linear antara fitur dan label lemah atau tidak ada.
- Saat nilai fitur dikelompokkan.
Pengelompokan bisa terasa kontra-intuitif, mengingat bahwa model dalam contoh sebelumnya memperlakukan nilai 37 dan 115 secara identik. Tapi ketika fitur tampak lebih kaku daripada linear, binning adalah cara yang jauh lebih baik untuk mewakili data.
Contoh pengelompokan: jumlah pembeli versus suhu
Misalkan Anda membuat model yang memprediksi jumlah pembeli berdasarkan suhu luar pada hari tersebut. Berikut adalah plot versus jumlah pembeli:
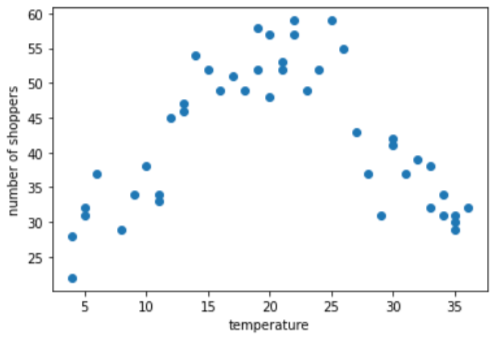
Plot menunjukkan, tidak mengherankan, bahwa jumlah pembeli tertinggi ketika suhu yang paling nyaman.
Anda dapat menyatakan fitur sebagai nilai mentah: suhu 35,0 di akan menjadi 35,0 dalam vektor fitur. Apa itu ide yang terbaik?
Selama pelatihan, model regresi linear mempelajari satu bobot untuk setiap aplikasi baru. Oleh karena itu, jika suhu direpresentasikan sebagai fitur tunggal, maka 35,0 akan memiliki lima kali pengaruh (atau seperlima pengaruh) dalam prediksi sebagai suhu 7,0. Namun demikian, plot tidak benar-benar menunjukkan hubungan linier antara label dan nilai fitur.
Grafik ini menyarankan tiga klaster dalam subrentang berikut:
- Bin 1 adalah kisaran suhu 4-11.
- Bin 2 adalah rentang suhu 12-26.
- Bin 3 adalah kisaran suhu 27-36.

Model ini mempelajari bobot terpisah untuk setiap kelompok.
Meskipun memungkinkan untuk membuat lebih dari tiga {i>bin<i}, bahkan satu {i>bin<i} terpisah untuk setiap pembacaan suhu, ini sering kali merupakan ide yang buruk karena alasan berikut:
- Model hanya bisa mempelajari asosiasi antara bin dan label jika ada yang memiliki cukup contoh. Pada contoh yang diberikan, masing-masing dari 3 bin berisi setidaknya 10 contoh, yang mungkin cukup untuk pelatihan. Dengan 33 {i>bin <i}terpisah, tidak ada satu pun {i>bin<i} yang berisi cukup contoh untuk model yang akan dilatih.
- Tempat terpisah untuk setiap suhu menghasilkan 33 fitur suhu terpisah. Namun, sebaiknya Anda meminimalkan jumlah fitur dalam model.
Latihan: Memeriksa pemahaman Anda
Plot berikut menunjukkan rata-rata harga rumah untuk setiap 0,2 derajat lintang untuk negara mitos Freedonia:
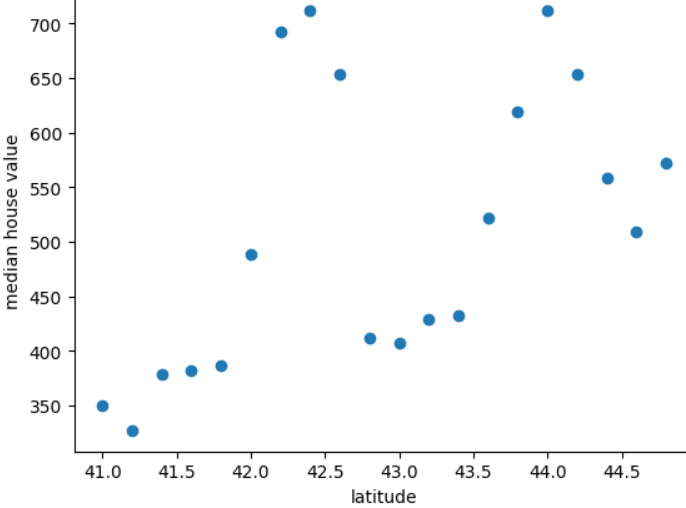
Grafik menunjukkan pola nonlinier antara nilai rumah dan lintang, sehingga merepresentasikan garis lintang sebagai nilai floating point-nya tidak akan membantu model membuat prediksi yang baik. Mungkin garis lintang pengelompokan akan lebih baik ide?
- 41,0 hingga 41,8
- 42,0 hingga 42,6
- 42,8 hingga 43,4
- 43,6 hingga 44,8
Pengelompokkan Kuantil
Bucketing kuantil membuat batas pengelompokan sehingga jumlah contoh di setiap bucket sama persis atau hampir sama. Pengelompokan kuantil kebanyakan yang menyembunyikan {i>outlier.<i}
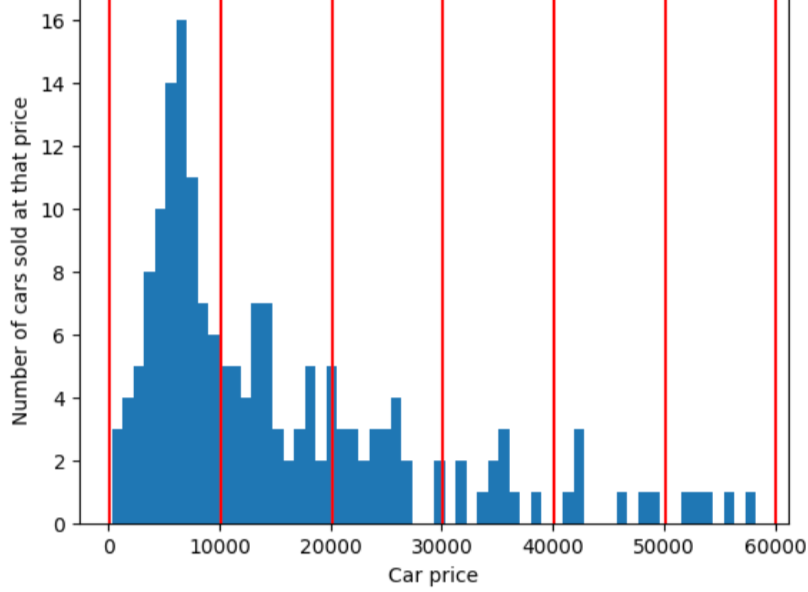
Untuk menggambarkan masalah yang dapat diselesaikan oleh bucketing kuantil, pertimbangkan bucket dengan jarak yang sama yang ditunjukkan dalam gambar berikut, di mana masing-masing dari sepuluh ember mewakili kisaran dengan tepat 10.000 dolar. Perhatikan bahwa bucket dari 0 hingga 10.000 berisi lusinan contoh tetapi bucket dari 50.000 hingga 60.000 hanya berisi 5 contoh. Akibatnya, model memiliki cukup contoh untuk dilatih pada 0 hingga 10.000 tetapi jumlah contoh yang ada tidak cukup untuk dilatih pada bucket 50.000 hingga 60.000.
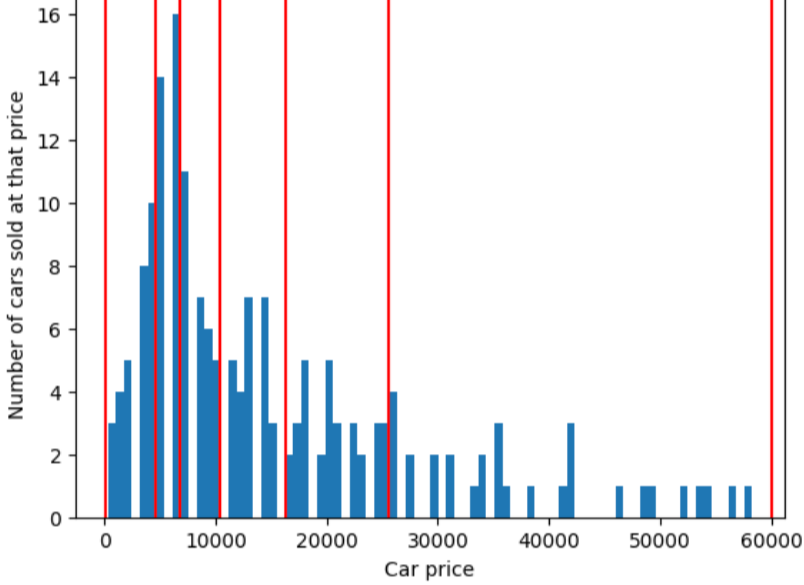
Sebaliknya, gambar berikut menggunakan bucketing kuantil untuk membagi harga mobil ke dalam {i>bin<i} dengan jumlah contoh yang kira-kira sama di setiap {i>bucket<i}. Perhatikan bahwa beberapa bin mencakup rentang harga yang sempit sementara yang lain mencakup rentang harga yang sangat luas.