Binning (נקרא גם יצירת קטגוריות) הוא
הנדסת תכונות
שמקבצת תתי-טווח מספריים שונים לתאונים
קטגוריות.
במקרים רבים, bining הופך נתונים מספריים לנתונים קטגוריים.
לדוגמה, נבחן תכונה
בשם X שהערך הנמוך ביותר שלו הוא 15 ו
הערך הגבוה ביותר הוא 425. באמצעות binning, אפשר לייצג את X עם
חמשת התאים הבאים:
- סל 1: 15 עד 34
- סל 2: 35 עד 117
- סל 3: 118 עד 279
- סל 4: 280 עד 392
- סל 5: 393 עד 425
סל 1 מתפרס על הטווח של 15 עד 34, כך שכל ערך של X בין 15 ל-34
מגיע לסל 1. מודל שאומן לפי מאגרי האשפה האלה לא יגיב בצורה שונה
ל-X ערכים של 17 ו-29 כי שני הערכים נמצאים ב-Bin 1.
וקטור התכונות מייצג את חמשת התאים הבאים:
| מספר סל | טווח | וקטור התכונה |
|---|---|---|
| 1 | 15-34 | [1.0, 0.0, 0.0, 0.0, 0.0] |
| 2 | 35-117 | [0.0, 1.0, 0.0, 0.0, 0.0] |
| 3 | 118-279 | [0.0, 0.0, 1.0, 0.0, 0.0] |
| 4 | 280-392 | [0.0, 0.0, 0.0, 1.0, 0.0] |
| 5 | 393-425 | [0.0, 0.0, 0.0, 0.0, 1.0] |
למרות ש-X היא עמודה יחידה במערך הנתונים, קישור גורמת למודל
כדי להתייחס ל-X כאל חמש תכונות נפרדות. לכן המודל לומד
משקולות נפרדות לכל פח.
Binning הוא חלופה טובה להתאמה לעומס (scaling) או חיתוך כאשר אחד התנאים הבאים מתקיימים:
- הקשר הלינארי הכולל בין התכונה לבין התווית חלשה או לא קיימת.
- כשהערכים של התכונות מקובצים באשכולות.
Binning עלול להרגיש שהוא לא הגיוני, בהינתן שהמודל בדוגמה הקודמת מתייחסים לערכים 37 ו-115 באופן זהה. אבל כאשר תכונה נראית גושית יותר מאשר לינארית, היא דרך הרבה יותר טובה שמייצגים את הנתונים.
דוגמה לצמצום: מספר הקונים לעומת מספר הקונים לעומת הטמפרטורה
נניח שאתם יוצרים מודל שחוזה את מספר קונים לפי הטמפרטורה בחוץ באותו יום. הנה עלילה הטמפרטורה לעומת מספר הקונים:
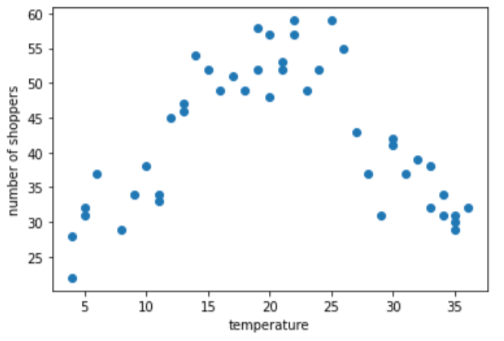
העלילה מראה, באופן לא מפתיע, שמספר הקונים היה הגבוה ביותר כאשר הטמפרטורה הייתה הכי נוחה.
אפשר לייצג את התכונה כערכים גולמיים: טמפרטורה של 35.0 מערך הנתונים יהיה 35.0 בווקטור המאפיין. האם זה הרעיון הכי טוב?
במהלך האימון, מודל רגרסיה ליניארית לומד משקל אחד לכל אחד מהם . לכן, אם הטמפרטורה מיוצגת כמאפיין יחיד, של 35.0, תהיה השפעה פי חמישה (או חמישית השפעה) בחיזוי כטמפרטורה של 7.0. עם זאת, בעלילה להראות קשר ליניארי כלשהו בין התווית .
התרשים מציע שלושה אשכולות בתת-טווחי המשנה הבאים:
- סל 1 הוא טווח הטמפרטורות 4-11.
- סל 2 הוא טווח הטמפרטורות 12-26.
- סל 3 הוא טווח הטמפרטורות 27-36.
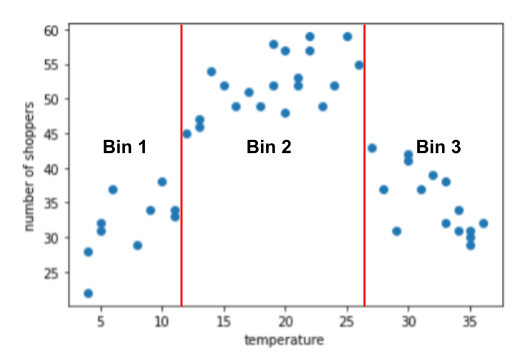
המודל לומד משקלים נפרדים לכל פח.
למרות שניתן ליצור יותר משלושה תאי תאים, גם סל נפרד כל ערך של טמפרטורה, לרוב זה רעיון לא טוב מהסיבות הבאות:
- המודל יכול ללמוד על הקשר בין סל לבין תווית רק אם יש מספיק דוגמאות בפח הזה. בדוגמה שלמעלה, כל אחד מ-3 תאי הפח מכיל לפחות 10 דוגמאות, ועשויות להספיק לאימון. עם 33 סלים נפרדים, אף אחד מהמאגרים לא יכיל מספיק דוגמאות כדי שהמודל יוכל להתאמן עליו.
- תא נפרד לכל טמפרטורה יוביל 33 תכונות נפרדות של הטמפרטורה. עם זאת, בדרך כלל כדאי למזער מספר התכונות במודל.
תרגיל: בדקו את ההבנה שלכם
בתרשים הבא מוצג מחיר הבית החציוני לכל 0.2 מעלות של קו הרוחב של המדינה המיתית פרידוניה:
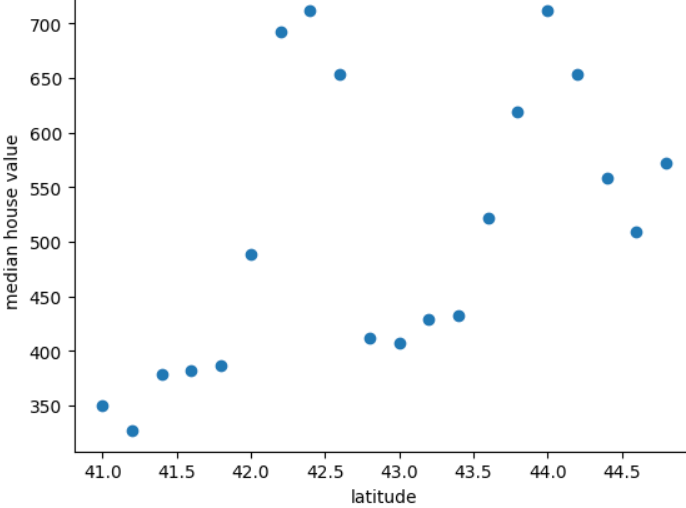
הגרפיקה מציגה דפוס לא ליניארי בין ערך הבית וקו הרוחב, לכן סביר להניח שייצוג של קו רוחב כערך הנקודה הצפה שלו לא יעזור של מודל מסוים הוא יכול להפיק חיזויים טובים. אולי עדיף לקבץ קווי רוחב רעיון?
- 41.0 עד 41.8
- 42.0 עד 42.6
- 42.8 עד 43.4
- 43.6 עד 44.8
סיווג לפי כמות
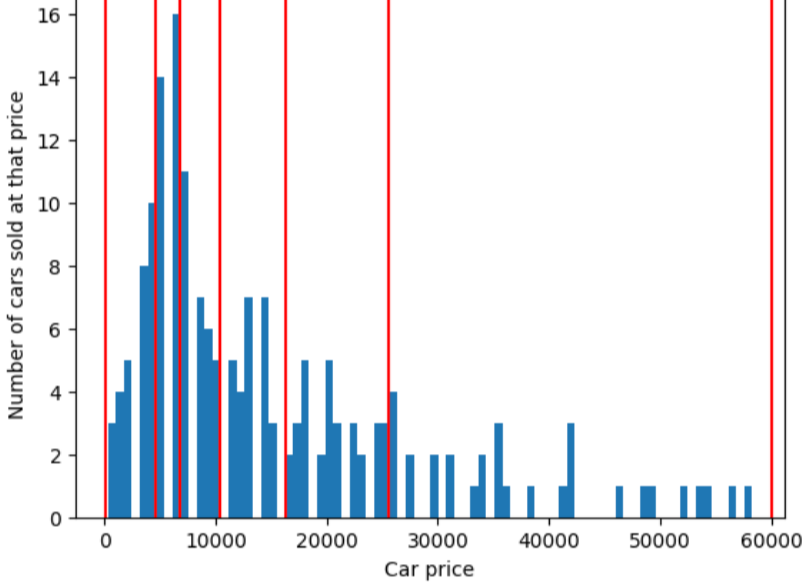
חלוקה לקטגוריות יוצרת גבולות לסיווג, כך שהמספר בכל קטגוריה היא שווה בדיוק או כמעט שווה. סיווג של כמותמים מסתיר בעיקר את נקודות החריגה.
כדי להמחיש את הבעיה שפותרת חלוקה לקטגוריות, נבחן את של הקטגוריות המרווחים באופן שווה, מוצגות באיור הבא, כאשר כל מתוך עשר הקטגוריות, מייצג טווח של 10,000 דולרים בדיוק. שימו לב שהקטגוריה מ-0 עד 10,000 מכילה עשרות דוגמאות אבל הקטגוריה מ-50,000 עד 60,000 מכילה רק 5 דוגמאות. לכן יש למודל מספיק דוגמאות כדי לאמן את הטווח שבין 0 ל-10,000 אבל אין מספיק דוגמאות לאימון עבור קטגוריה של 50,000 עד 60,000.
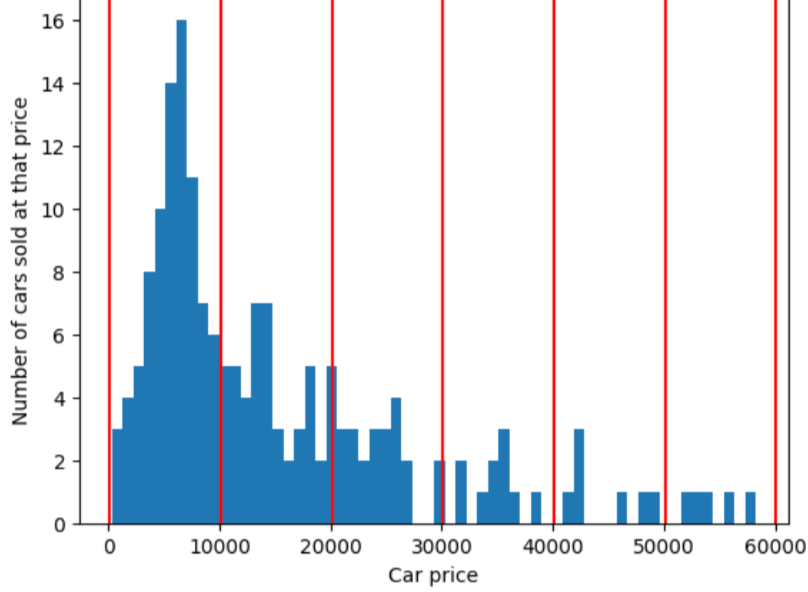
לעומת זאת, האיור הבא משתמש בסיווג כמותיים כדי לחלק את מחירי המכוניות לתאים עם אותו מספר של דוגמאות בכל קטגוריה. שימו לב שחלק מפחי האשפה כוללים טווח מחירים צר, ואילו אחרים מקיפים טווח מחירים רחב מאוד.