Групування (інша назва – сегментація) – це метод конструювання ознак, який об’єднує різні числові піддіапазони в секції або сегменти.
У багатьох випадках групування перетворює числові дані на категорійні.
Наприклад, розгляньмо ознаку X, мінімальне й максимальне значення якої становлять 15 і 425 відповідно. Використовуючи групування, можна представити X як п’ять секцій.
- Секція 1: 15–34
- Секція 2: 35–117
- Секція 3: 118–279
- Секція 4: 280–392
- Секція 5: 393–425
Секція 1 охоплює діапазон 15–34, тому кожне значення X від 15 до 34 потрапляє в неї. Модель, навчена на цих секціях, реагуватиме однаково на значення X 17 і 29, оскільки обидва містяться в секції 1.
Вектор ознак утворює п’ять секцій, наведених нижче.
| Номер секції | Діапазон | Вектор ознак |
|---|---|---|
| 1 | 15–34 | [1.0, 0.0, 0.0, 0.0, 0.0] |
| 2 | 35–117 | [0.0, 1.0, 0.0, 0.0, 0.0] |
| 3 | 118–279 | [0.0, 0.0, 1.0, 0.0, 0.0] |
| 4 | 280–392 | [0.0, 0.0, 0.0, 1.0, 0.0] |
| 5 | 393–425 | [0.0, 0.0, 0.0, 0.0, 1.0] |
Навіть якщо X у наборі даних представлено одним стовпцем, через групування модель розглядає X як п’ять окремих ознак. Тому модель запам’ятовує окремі значення ваги для кожної секції.
Групування – хороша заміна масштабуванню або обрізанню, якщо виконується будь-яка з умов, наведених нижче.
- Загальний лінійний зв’язок між ознакою і міткою слабкий або взагалі відсутній.
- Значення ознак кластеризовано.
Спершу групування може видаватися нелогічним з огляду на те, що модель у попередньому прикладі сприймає значення 37 і 115 однаково. Але коли ознака – не лінійна, а скоріше група значень, групування – набагато кращий спосіб представлення даних.
Приклад групування: кількість покупців залежно від температури повітря
Уявімо, що ви створюєте модель, яка прогнозує кількість покупців за даними про температуру на вулиці в цей день. Нижче наведено графік співвідношення температури й кількості покупців.
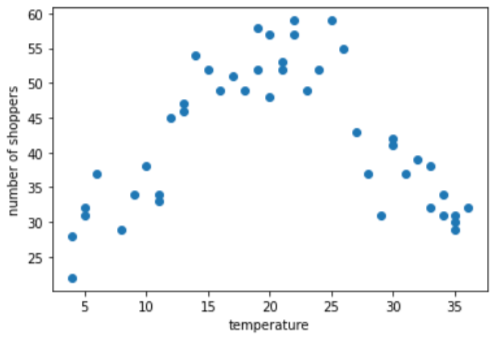
На графіку показано, що кількість покупців була найвищою, коли температура була максимально комфортною, і це не дивно.
Можна представити ознаку у вигляді необроблених значень: температура 35,0 у наборі даних становитиме 35,0 у векторі ознак. Чи це найкращий варіант?
Під час навчання модель лінійної регресії запам’ятовує єдине значення ваги для кожної ознаки. Отже, якщо температуру представлено як єдину ознаку, то значення 35,0 впливатиме на прогноз у п’ять разів більше (становитиме 1/5 впливу), ніж 7,0. Хоча на графіку не видно лінійної залежності між міткою і значенням ознаки.
На графіку можна виділити три кластери в піддіапазонах, наведених нижче.
- Секція 1: діапазон температури 4–11.
- Секція 2: діапазон температури 12–26.
- Секція 3: діапазон температури 27–36.
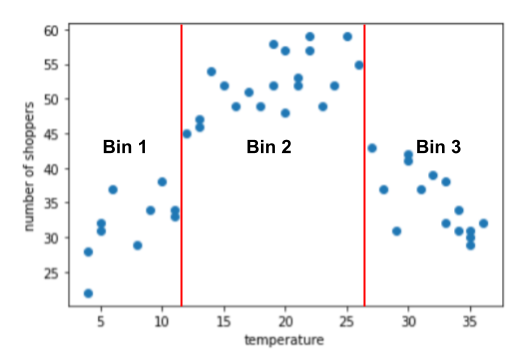
Модель запам’ятовує окремі значення ваги для кожної секції.
Хоча можна створити більше ніж три секції (навіть по одній для кожного значення температури), часто це недоцільно з причин, наведених нижче.
- Модель може вивчати зв’язок між секцією і міткою лише тоді, коли в секції достатньо прикладів. У наведеній моделі кожна з трьох секцій містить щонайменше 10 прикладів, яких може бути достатньо для навчання. Якщо секцій буде 33, то серед них не виявитися тої, яка має достатньо прикладів для навчання моделі.
- Якщо для кожної температури використовувати окрему секцію, отримаємо 33 окремі ознаки температури. Однак зазвичай слід мінімізувати кількість ознак у моделі.
Вправа. Перевірте свої знання
На графіку нижче показано середню ціну на житло для кожних 0,2 градуса широти в гіпотетичній країні Фридонії.
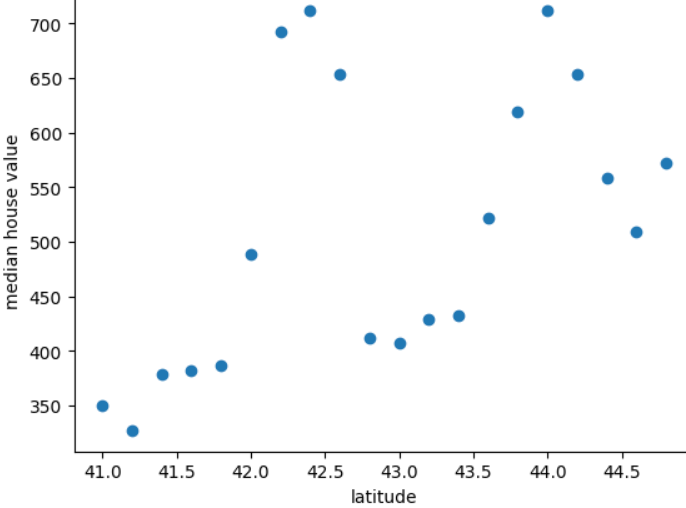
На графіку показано нелінійну залежність між вартістю житла й широтою, тому представлення широти як значення з рухомою комою навряд чи допоможе моделі робити хороші прогнози. Можливо, краще використовувати сегментацію значень широти?
- 41,0–41,8
- 42,0–42,6
- 42,8–43,4
- 43,6–44,8
Квантильна сегментація
Квантильна сегментація розмежовує сегменти так, щоб кількість прикладів у кожному з них була абсолютно або майже однаковою, і здебільшого приховує викиди.
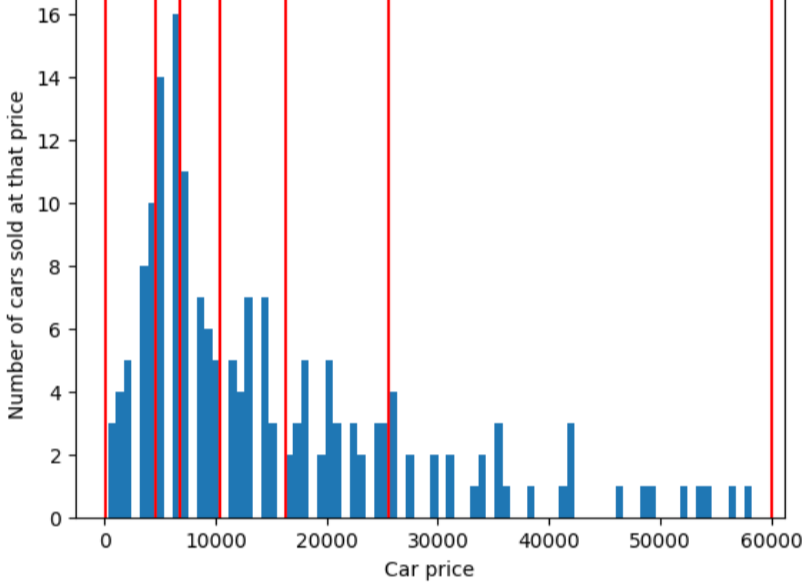
Щоб унаочнити проблему, яку вирішує квантильна сегментація, розгляньмо рівномірно розташовані сегменти, показані на рисунку нижче, де кожен із десяти сегментів – діапазон, що становить рівно 10 000 доларів. Зверніть увагу, що в сегменті 0–10 000 є десятки прикладів, а в сегменті 50 000–60 000 – лише п’ять. Отже, модель має достатньо прикладів для навчання на сегменті 0–10 000, але замало, щоб тренуватися на сегменті 50 000–60 000.
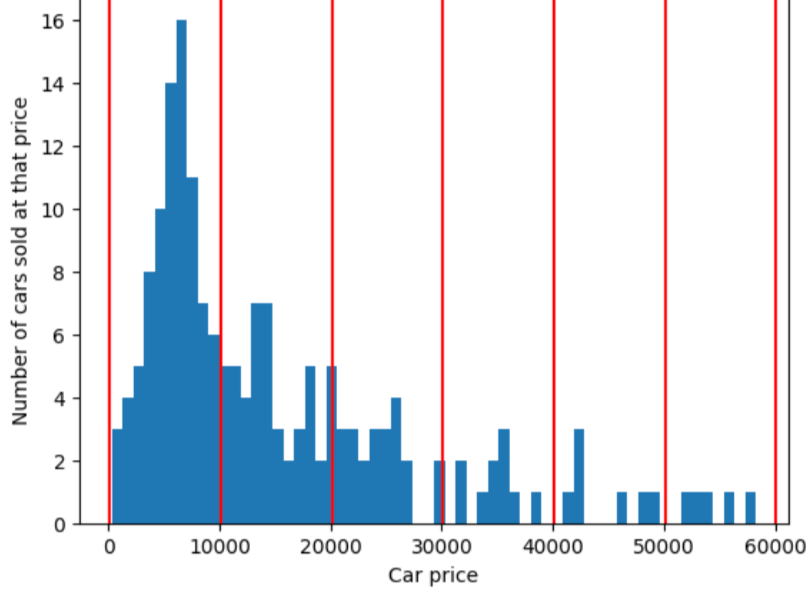
Тимчасом на наступному рисунку використовується квантильна сегментація для розподілу цін на автомобілі в сегменти з приблизно однаковою кількістю прикладів у кожному з них. Зверніть увагу, що одні сегменти покривають вузький ціновий діапазон, а інші – дуже широкий.