Binning (也稱為「值區」) 是
特徵工程
可將不同的數值子範圍分為「bins」或
buckets。
在許多情況下,繫結會將數值資料轉換為類別型資料。
舉例來說,考慮功能
名為 X,最低值為 15 且
最高的值為 425使用繫結功能,您就能以下列項目表示 X:
以下五個特徵分塊:
- 特徵分塊 1:15 至 34
- 特徵分塊 2:35 至 117
- 特徵分塊 3:118 至 279
- 特徵分塊 4:280 至 392
- 5:393 至 425
特徵分塊 1 的範圍涵蓋 15 到 34,因此 X 的所有值介於 15 到 34 之間
最終在作業區 1以這些特徵分塊訓練的模型不會有任何反應
設為 17 和 29 的 X 值,因為這兩個值都位於 Bin 1。
特徵向量代表 五個特徵分塊,如下所示:
| 特徵分塊號碼 | 範圍 | 特徵向量 |
|---|---|---|
| 1 | 15-34 歲 | [1.0、0.0、0.0、0.0、0.0] |
| 2 | 35-117 歲 | [0.0、1.0、0.0、0.0、0.0] |
| 3 | 118-279 人 | [0.0、0.0、1.0、0.0、0.0] |
| 4 | 280-392 人 | [0.0、0.0、0.0、1.0、0.0] |
| 5 | 第 393 至 425 天 | [0.0、0.0、0.0、0.0、1.0] |
雖然 X 是資料集中的單一資料欄,但繫結會導致模型
將 X 視為五個獨立功能。因此模型會學習
為每個特徵分塊單獨權重;
特徵繫結是資源調度的理想替代方案 或裁剪系統 符合下列條件:
- 特徵和整體線性關係 label 錯誤或不存在。
- 將特徵值分群時。
特徵分塊可能會產生違反直覺,因為 先前的範例會將值 37 和 115 視為相同的處理方式。但當場 特徵似乎比線性關係更完整,因此若選擇特徵, 代表資料
特徵分塊範例:購物者人數與溫度
假設您建立的模型會預測 當天的戶外溫度,吸引購物者。以下是 溫度與購物者人數:

這個圖表顯示,當時購物者數量最多 是最舒適的溫度
您可以將特徵表示為原始值: 在特徵向量中是 35.0這個想法是否正確?
在訓練期間,線性迴歸模型會學習 而不是每個特徵的分數因此,如果隨機性參數是以單一特徵表示, 就等於 35.0 度可能成為影響因素的五倍 以 7.0 的溫度計費但本圖沒有 真正會顯示標籤和 特徵值
這張圖表建議下列子範圍有三個叢集:
- 特徵分塊 1 表示溫度範圍為 4 到 11。
- 特徵區間 2 的溫度範圍為 12-26。
- 特徵區間 3 的溫度範圍為 27-36。

這個模型會學習每個特徵分塊的權重。
雖然您可建立超過 3 個特徵分塊 這個想法經常產生錯誤,原因如下:
- 只有在包含特徵分塊和標籤的情況下,模型才能得知 都有足夠的範例在此範例中,3 個特徵分塊 至少包含 10 個樣本,可能已足以用於訓練。 分為 33 個特徵分塊 所有特徵分塊包含的樣本都不足以訓練模型。
- 每個隨機性參數的特徵分塊 33 種不同溫度功能。不過,建議您通常將最小化 例如模型的特徵數量
練習:隨堂測驗
下圖顯示每 0.2 度的房價中位數 神話自由國的緯度:
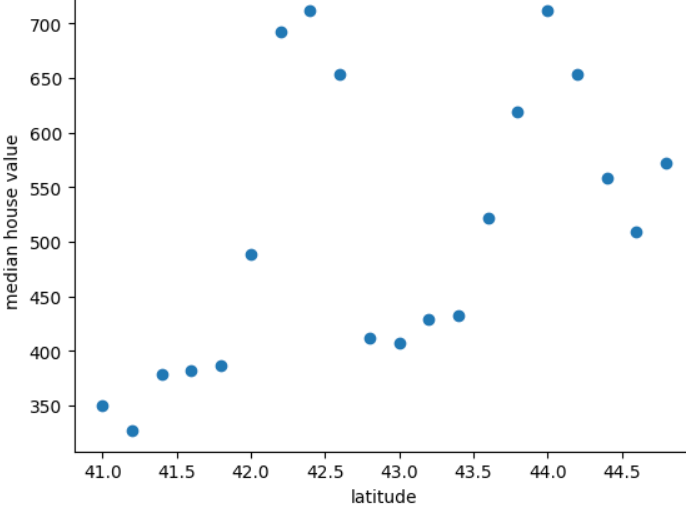
此圖片顯示房屋值和緯度之間的非線性模式, 因此將緯度視為浮點值不太可能對 如何產生良好預測也許是將定位緯度 好嗎?
- 41.0 至 41.8
- 42.0 至 42.6
- 42.8 至 43.4
- 43.6 至 44.8
分四特徵分塊
分位數值區會建立特徵分塊,以達到這個目標 每個區間的範例都完全或幾乎等於分四分塊 大多會隱藏離群值
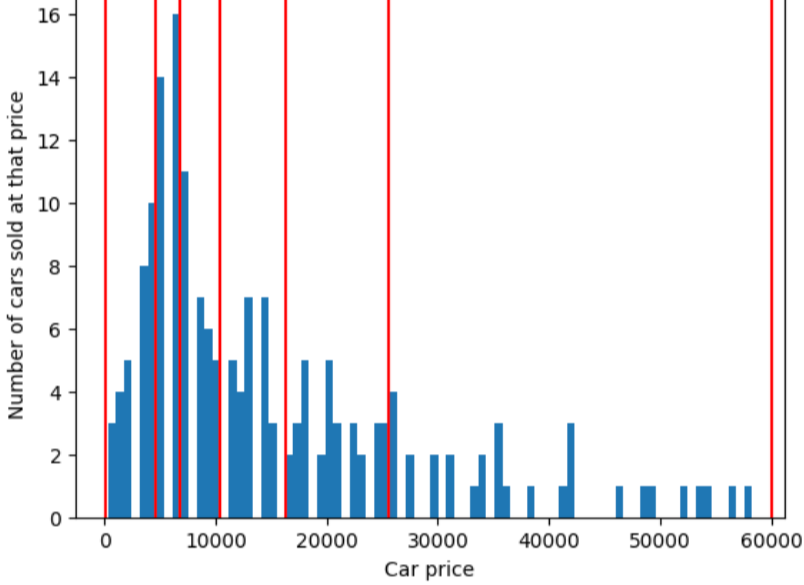
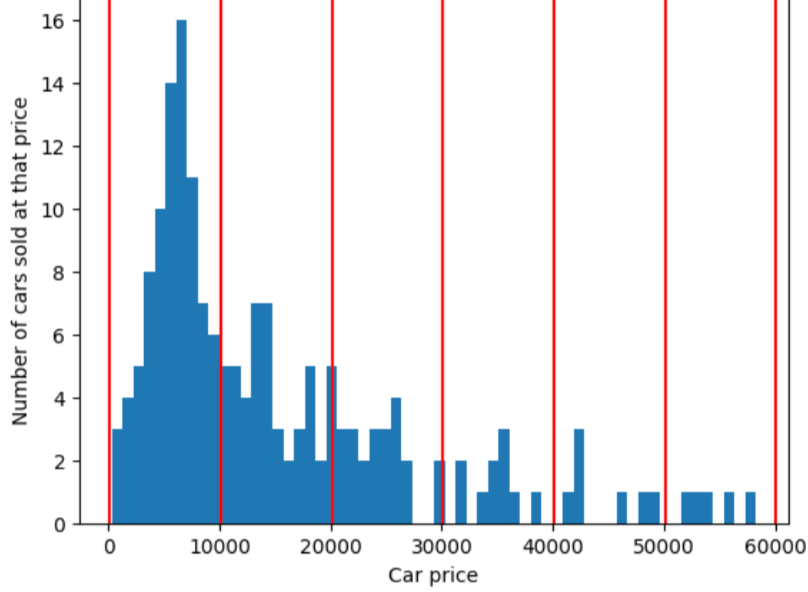
為了說明分量特徵分塊解決的問題,請考慮 如下圖所示,每個值區都含有相同間距 的 10 個區間代表正好 10,000 美元的時距。 請注意,從 0 到 10,000 的值區包含數十個範例 但從 50,000 到 60,000 個值區僅包含 5 個範例 因此,模型已擁有足夠的樣本,可以在 0 至 10,000 時進行訓練 卻不足以針對 50,000 至 60,000 個值區進行訓練。
相較之下,下圖使用分位數值區來劃分車輛價格 轉換為特徵分塊,且每個值區中的範例數量大致相同。 請注意,某些特徵分塊的價格範圍較小,其他特徵分塊 代表價格的區間可能非常廣泛