透過統計和視覺化技術檢查資料後,您應轉換資料,協助模型更有效率地訓練。正規化的目標是轉換特徵,使其測量尺度相近。舉例來說,請考量下列兩項特徵:
- 特徵
X的範圍為 154 至 24,917,482。 - 特徵
Y的範圍為 5 到 22。
這兩項功能涵蓋的範圍差異很大。正規化可能會操縱 X 和 Y,使它們涵蓋類似的範圍,例如 0 到 1。
正規化有以下優點:
- 有助於模型在訓練期間更快收斂。如果不同特徵的範圍不同,梯度下降可能會「反彈」,導致收斂速度變慢。不過,Adagrad 和 Adam 等更進階的最佳化工具,會隨著時間改變有效學習率,以防範這個問題。
- 協助模型推斷更準確的預測結果。 如果不同特徵的範圍不同,產生的模型預測結果可能就比較不實用。
- 有助於在特徵值非常高時避免「NaN 陷阱」。NaN 是「不是數字」的縮寫,如果模型中的值超過浮點數精確度上限,系統會將值設為
NaN,而非數字。當模型中的某個數字變成 NaN 時,模型中的其他數字最終也會變成 NaN。 - 協助模型學習各個特徵的適當權重。如果沒有特徵縮放,模型會過度著重於範圍較廣的特徵,而對範圍較窄的特徵不夠重視。
建議您將涵蓋明顯不同範圍的數值特徵 (例如年齡和收入) 正規化。我們也建議將涵蓋廣泛範圍的單一數值特徵正規化,例如 city population.
請考慮下列兩項功能:
- 特徵「
A」的最低值為 -0.5,最高值為 +0.5。 - 特徵
B的最低值為 -5.0,最高值為 +5.0。
「特徵 A」和「特徵 B」的範圍相對較窄。不過,特徵 B 的範圍是特徵 A 範圍的 10 倍。因此:
- 在訓練開始時,模型會假設特徵
B的「重要性」是特徵A的十倍。 - 訓練時間會比預期長。
- 產生的模型可能不盡理想。
未標準化造成的整體損害相對較小,但我們仍建議將特徵 A 和特徵 B 標準化為相同比例,例如 -1.0 到 +1.0。
現在,請考慮範圍差異較大的兩項特徵:
- 特徵「
C」的最低值為 -1,最高值為 +1。 - 特徵「
D」的最低值為 +5000,最高值為 +1,000,000,000。
如果沒有將特徵 C 和特徵 D 正規化,模型很可能無法達到最佳狀態。此外,訓練會花費更長的時間才能收斂,甚至可能完全無法收斂!
本節將介紹三種常見的正規化方法:
- 線性縮放
- 標準分數縮放
- 對數縮放
本節也會說明剪輯功能。雖然剪除並非真正的正規化技術,但確實能將不規律的數值特徵限制在特定範圍內,進而產生更優質的模型。
線性調整
線性縮放 (通常簡稱為縮放) 是指將浮點值從自然範圍轉換為標準範圍,通常是 0 到 1 或 -1 到 +1。
如果符合下列所有條件,就很適合使用線性調度:
- 資料的上下限不會隨著時間大幅變動。
- 特徵包含極少或沒有離群值,且這些離群值並非極端值。
- 這項特徵大致平均分布在範圍內。 也就是說,直方圖中大部分的值都會顯示大致相同的長條。
假設「human」age 是特徵。線性縮放是 age 的良好正規化技術,原因如下:
- 大約介於 0 到 100 之間。
age包含的離群值比例相對較小。只有約 0.3% 的人口超過 100 歲。- 雖然某些年齡層的代表性較高,但大型資料集應包含所有年齡層的充足範例。
練習:確認您的理解程度
假設您的模型有名為net_worth 的特徵,其中包含不同人士的淨值。線性縮放是否適合用來正規化 net_worth?原因為何?
標準分數縮放
Z 分數是指某個值與平均值之間相差幾個標準差。舉例來說,如果某個值比平均值大 2 個標準差,則 Z 分數為 +2.0。如果某個值比平均值少 1.5 個標準差,則 Z 分數為 -1.5。
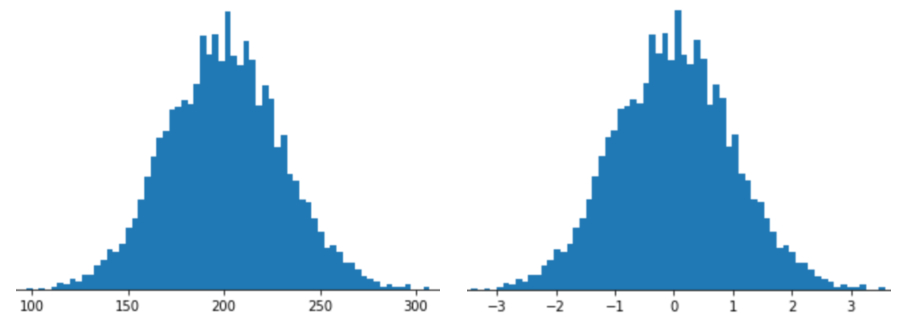
以 Z 分數縮放表示特徵,是指將該特徵的 Z 分數儲存在特徵向量中。舉例來說,下圖顯示兩個直方圖:
- 左側是傳統常態分佈。
- 右側是經過 Z 分數縮放正規化的相同分布。
對於僅略呈常態分布的資料 (如下圖所示),Z 分數縮放也是不錯的選擇。
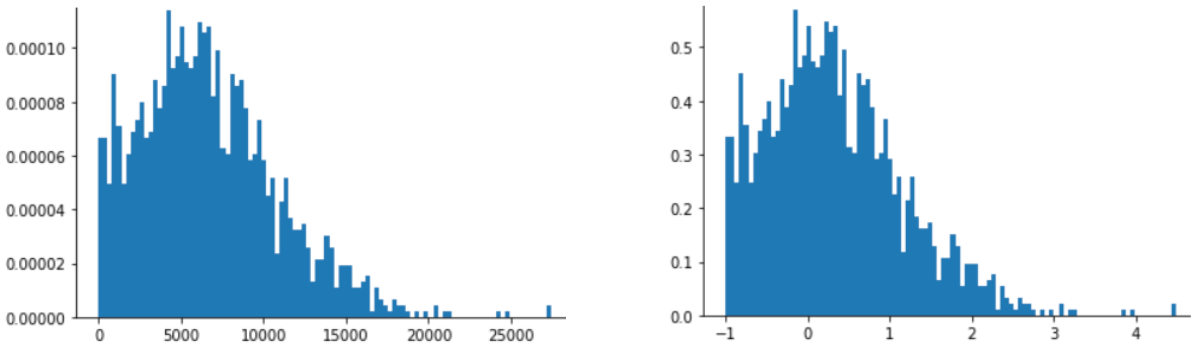
如果資料遵循常態分布或類似常態分布的分布,Z 分數就是不錯的選擇。
請注意,某些分布情形可能在大部分範圍內都屬於正常,但仍包含極端離群值。舉例來說,net_worth 特徵中幾乎所有點都可能落在 3 個標準差內,但這項特徵的幾個例子可能與平均值相差數百個標準差。在這種情況下,您可以結合 Z 分數縮放和另一種形式的正規化 (通常是裁剪),以處理這種情況。
練習:確認您的理解程度
假設模型訓練的特徵名為height,其中包含一千萬名女性的成人身高。Z 分數縮放是否適合用來正規化 height?原因為何?
記錄縮放
對數縮放會計算原始值的對數。理論上,對數可以是任何底數;但實際上,對數縮放通常會計算自然對數 (ln)。
如果資料符合冪律分布,對數縮放功能就很有幫助。 以簡單的說法來說,冪律分布如下所示:
X的值越低,Y的值就越高。X的值增加時,Y的值會快速減少。因此,X的值越高,Y的值就越低。
電影分級就是冪律分布的絕佳例子。在下圖中,請注意:
- 有些電影獲得許多使用者評分。(
X值越低,Y值越高)。 - 大多數電影的使用者評分很少。(
X的值越高,Y的值就越低。)
記錄縮放會改變分布情形,有助於訓練模型,進而做出更準確的預測。

以書籍銷售為例,由於以下原因,書籍銷售量符合冪律分布:
- 大多數出版書籍的銷量極低,可能只有一、兩百本。
- 有些書籍的銷量適中,約有數千本。
- 只有少數暢銷書的銷量會超過一百萬本。
假設您要訓練線性模型,找出書籍封面與書籍銷售量之間的關係。如果線性模型是根據原始值訓練,就必須找出銷售量達一百萬本的書籍封面,其影響力比銷售量僅 100 本的書籍封面高出 10,000 倍。不過,如果將所有銷售數據都進行對數縮放,這項工作就變得可行多了。 舉例來說,100 的對數為:
~4.6 = ln(100)
而 1,000,000 的對數為:
~13.8 = ln(1,000,000)
因此,1,000,000 的對數只比 100 的對數大約多三倍。您可能可以想像,暢銷書的封面比銷售量極低的書籍封面強大 (在某方面) 約三倍。
剪輯
剪除是一種技術,可盡量減少極端離群值的影響。簡單來說,剪除通常會將離群值的上限設為特定最大值,藉此降低離群值。剪輯是個奇怪的想法,但卻非常有效。
舉例來說,假設資料集包含名為 roomsPerPerson 的特徵,代表各個房屋的房間數量 (總房間數除以居住人數)。下圖顯示超過 99% 的特徵值符合常態分佈 (平均值約為 1.8,標準差為 0.7)。不過,這項功能包含一些離群值,其中有些是極端值:
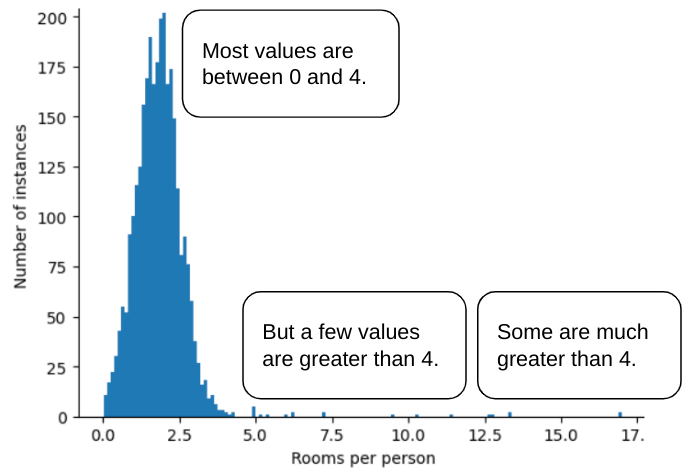
如何盡量減少這些極端離群值的影響?嗯,直方圖並非均勻分布、常態分布或冪律分布。如果只是將 roomsPerPerson 的最大值設為上限或裁剪為任意值 (例如 4.0),會發生什麼情況?
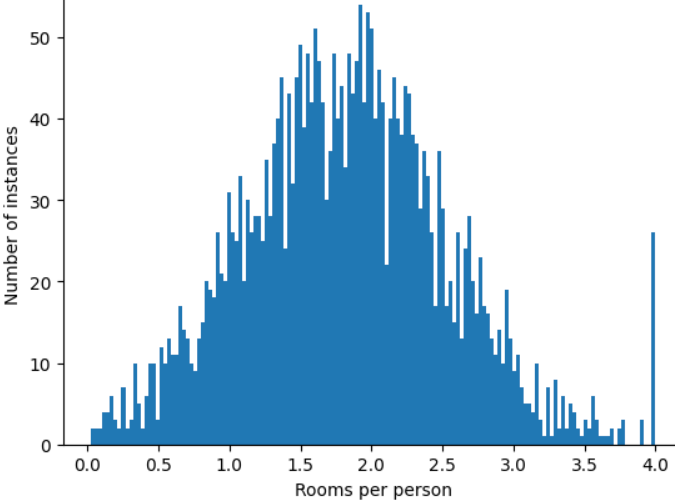
將特徵值剪輯為 4.0,並不代表模型會忽略所有大於 4.0 的值。而是指所有大於 4.0 的值現在都會變成 4.0。這說明瞭 4.0 的特殊山丘。儘管有這項限制,但縮放後的特徵集比原始資料更有用。
等等!您真的能將每個離群值都縮減為任意上限閾值嗎?訓練模型時需要。
您也可以在套用其他形式的正規化後,再剪除值。舉例來說,假設您使用 Z 分數縮放,但有幾個離群值的絕對值遠大於 3。在這種情況下,您可以:
- 將 Z 分數大於 3 的片段設為 3。
- 如果影片片段的 Z 分數低於 -3,系統會將其設為 -3。
剪輯功能可防止模型過度索引不重要的資料。不過,有些離群值其實很重要,因此請謹慎剪除值。
正規化技術摘要
| 正規化技術 | 公式 | 使用時機 |
|---|---|---|
| 線性調整 | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | 當特徵在範圍內大致均勻分布。 扁平狀 |
| 標準分數縮放 | $$ x' = \frac{x - μ}{σ}$$ | 當特徵呈常態分佈 (峰值接近平均值)。 鐘形 |
| 記錄縮放 | $$ x' = log(x)$$ | 當特徵分布在尾部的至少一側嚴重傾斜時。Heavy Tail-shaped |
| 剪輯 | 如果 $x > max$,請將 $x' = max$ 如果 $x < min$,請將 $x' = min$ |
特徵包含極端離群值。 |
練習:測驗你的知識

假設您要開發模型,根據資料中心內測得的溫度預測資料中心的生產力。資料集中的 temperature 值幾乎都介於 15 到 30 (攝氏) 之間,但有以下例外狀況:
- 每年一到兩次,在極度炎熱的日子,
temperature會記錄到介於 31 到 45 之間的值。 temperature中的每 1,000 個點都會設為 1,000,而非實際溫度。
下列何者是合理的正規化技術?
temperature
1,000 的值是錯誤的,應刪除而非裁剪。
31 到 45 之間的值是合法資料點。 假設資料集在這個溫度範圍內沒有足夠的範例,可訓練模型做出良好的預測,那麼剪除這些值可能是不錯的做法。不過,在推論期間,請注意,因此,對於 45 度的溫度,裁剪後的模型會做出與 35 度溫度相同的預測。