Dopo aver esaminato i tuoi dati attraverso tecniche statistiche e di visualizzazione, è necessario trasformare i dati in modi che permettano di addestrare ulteriormente il modello in modo efficace. L'obiettivo normalizzazione è trasformare le caratteristiche su una scala simile. Ad esempio, considera i seguenti due caratteristiche:
- La funzionalità
Xcopre l'intervallo da 154 a 24.917.482. - La funzionalità
Ycomprende l'intervallo da 5 a 22.
Queste due caratteristiche coprono intervalli molto diversi. La normalizzazione potrebbe manipolare
X e Y in modo che coprano un intervallo simile, ad esempio da 0 a 1.
La normalizzazione offre i seguenti vantaggi:
- Aiuta i modelli a convergere più rapidamente durante l'addestramento. Quando caratteristiche diverse hanno intervalli diversi, la discesa del gradiente può "rimbalzare" e rallentare la convergenza. Detto questo, gli ottimizzatori più avanzati come Adagrad e Adam proteggono da questo problema modificando il tasso di apprendimento effettivo nel tempo.
- Aiuta i modelli a dedurre previsioni migliori. Quando caratteristiche diverse hanno intervalli diversi, modello potrebbe fare previsioni un po' meno utili.
- Aiuta a evitare il "trap NaN" quando i valori delle caratteristiche sono molto elevati.
NaN è l'abbreviazione di
not a number. Quando un valore in un modello supera il limite di precisione a virgola mobile, il sistema imposta il valore su
NaNanziché su un numero. Quando un numero nel modello diventa NaN, anche gli altri numeri nel modello diventano NaN. - Aiuta il modello ad apprendere i pesi appropriati per ogni caratteristica. Senza la scalabilità delle caratteristiche, il modello presta troppa attenzione alle caratteristiche con intervalli ampi e non c'è abbastanza attenzione alle caratteristiche con intervalli ristretti.
Consigliamo di normalizzare le caratteristiche numeriche che coprono intervalli distintamente diversi (ad esempio età e reddito).
Consigliamo inoltre di normalizzare una singola caratteristica numerica che copre un ampio intervallo,
come city population.
Considera le seguenti due funzionalità:
- Il valore più basso della caratteristica
Aè -0,5, mentre il più alto è +0,5. - Il valore minimo dell'elemento
Bè -5,0 e il valore massimo è +5,0.
La funzionalità A e la funzionalità B hanno intervalli relativamente stretti. Tuttavia, le funzionalità di B
l'intervallo è 10 volte più ampio dell'intervallo della caratteristica A. Pertanto:
- All'inizio dell'addestramento, il modello presuppone che la caratteristica
Asia dieci volte più "importante" rispetto alla funzionalitàB. - L'addestramento richiederà più tempo del previsto.
- Il modello risultante potrebbe non essere ottimale.
Il danno complessivo dovuto alla mancata normalizzazione sarà relativamente ridotto. ma consigliamo comunque di normalizzare le caratteristiche A e B sulla stessa scala, ad esempio da -1,0 a +1,0.
Ora prendi in considerazione due elementi con una disparità maggiore di intervalli:
- Il valore più basso della caratteristica
Cè -1, mentre il più alto è +1. - Il valore più basso della caratteristica
Dè +5000, mentre il massimo è +1.000.000.000.
Se non normalizzi le caratteristiche C e D, il modello probabilmente
non ottimale. Inoltre, l'addestramento richiederà
convergono o addirittura non riescono a convergere del tutto.
Questa sezione illustra tre metodi di normalizzazione molto utilizzati:
- scalabilità lineare
- Scalabilità punteggio z
- scalabilità dei log
Questa sezione tratta inoltre del taglio. Sebbene non sia un vero di normalizzazione, il clipping impedisce le caratteristiche numeriche indisciplinate che producono modelli migliori.
Scala lineare
La scalabilità lineare (più comunemente abbreviata in scalabilità) consiste nella conversione dei valori in virgola mobile dal loro intervallo naturale in un intervallo standard, in genere da 0 a 1 o da -1 a +1.
La scalabilità lineare è una buona scelta se si verificano tutte le seguenti condizioni:
- I limiti inferiore e superiore dei dati non cambiano molto nel tempo.
- La caratteristica contiene pochi o nessun outlier e questi valori non sono estrema.
- La funzionalità è distribuita in modo approssimativamente uniforme nell'intervallo. In altre parole, un istogramma mostrerebbe barre approssimativamente uniformi per la maggior parte dei valori.
Supponiamo che l'utente age sia una caratteristica. La scalabilità lineare è una buona normalizzazione
tecnica per age perché:
- I limiti inferiori e superiori approssimativi sono da 0 a 100.
agecontiene una percentuale relativamente piccola di outlier. Solo circa lo 0,3% della popolazione ha più di 100 anni.- Sebbene alcune età siano rappresentate meglio di altre, un insieme di dati di grandi dimensioni dovrebbe contenere esempi sufficienti di tutte le età.
Allenamento: verifica le tue conoscenze
Supponiamo che il modello abbia una caratteristica denominatanet_worth che contiene la rete
di persone diverse. La scalabilità lineare sarebbe una buona normalizzazione
per net_worth? Qual è il motivo?
Scalabilità punteggio z
Il punteggio z è il numero di deviazioni standard che un valore proviene dalla media. Ad esempio, un valore che è 2 deviazioni standard maggiori della media ha un valore Z pari a +2,0. Un valore inferiore di 1,5 deviazioni standard rispetto alla media ha un valore Z pari a -1,5.
Rappresentare una caratteristica con la scalatura del punteggio z significa memorizzare il punteggio z della caratteristica nel vettore di caratteristiche. Ad esempio, la figura seguente mostra due istogrammi:
- A sinistra, una distribuzione normale classica.
- A destra, la stessa distribuzione normalizzata per la scalatura del punteggio Z.
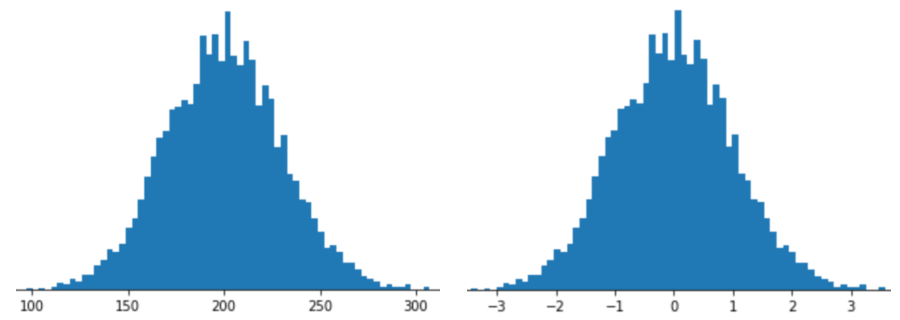
Anche la scalabilità del punteggio z è una buona scelta per dati come quelli mostrati nella figura seguente, che ha solo una distribuzione vagamente normale.
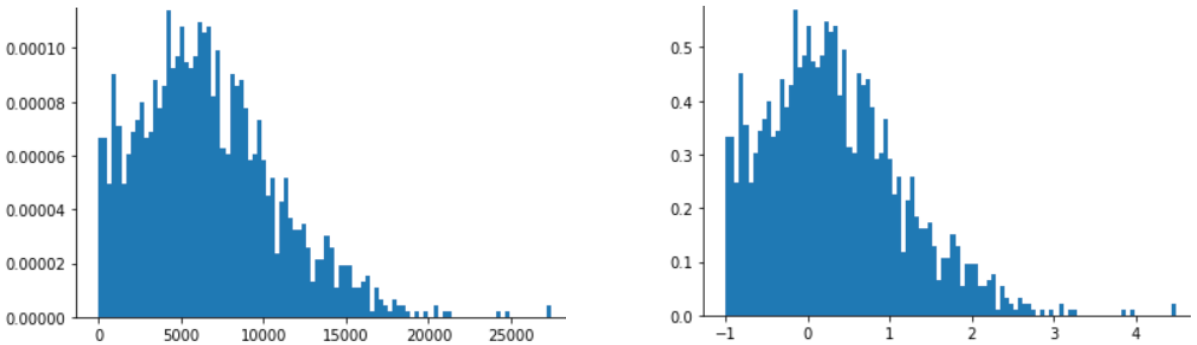
Lo z-score è una buona scelta quando i dati seguono una distribuzione normale o una distribuzione alquanto simile a una normale distribuzione.
Tieni presente che alcune distribuzioni potrebbero essere normali nella maggior parte del loro
intervallo, ma contenere comunque valori anomali estremi. Ad esempio, quasi tutti i punti di una caratteristica net_worth potrebbero rientrare perfettamente in tre deviazioni standard, ma alcuni esempi di questa caratteristica potrebbero essere a centinaia di deviazioni standard dalla media. In queste situazioni, è possibile combinare la scalabilità del punteggio Z con
un'altra forma di normalizzazione (di solito taglio) per gestire questa situazione.
Esercizio: verifica di aver compreso
Supponiamo che il tuo modello venga addestrato su una funzionalità denominataheight che contiene le altezze adulte di dieci milioni di donne. La scalatura del punteggio Z sarebbe una buona tecnica di normalizzazione per height? Qual è il motivo?
Scala logaritmica
La scalabilità dei log calcola il logaritmo del valore non elaborato. In teoria, il logaritmo può avere qualsiasi base; in pratica, la scala logaritmica di solito calcola il logaritmo naturale (ln).
La scalabilità dei log è utile quando i dati sono conformi a una distribuzione della legge dell'alimentazione. In termini informali, una distribuzione di legge di potenza ha il seguente aspetto:
- Valori bassi di
Xhanno valori molto alti diY. - Con l'aumento dei valori di
X, i valori diYdiminuiscono rapidamente. Di conseguenza, valori elevati diXhanno valori molto bassi diY.
Le classificazioni dei film sono un buon esempio di distribuzione della legge elettrica. Nella seguente figura, nota quanto segue:
- Alcuni film hanno molte valutazioni degli utenti. I valori bassi di
Xhanno valori elevati diY. - La maggior parte dei film ha pochissime valutazioni degli utenti. I valori elevati di
Xsono bassi valori diY.)
La scala logaritmica modifica la distribuzione, il che consente di addestrare un modello che effettuerà previsioni migliori.
Come secondo esempio, le vendite di libri sono conformi a una distribuzione di legge di potenza perché:
- La maggior parte dei libri pubblicati vende un numero esiguo di copie, forse una o duecento.
- Alcuni libri ne vendono un numero moderato, nell'ordine delle migliaia.
- Solo pochi bestseller vendono più di un milione di copie.
Supponiamo che tu stia addestrando un modello lineare per trovare la relazione tra, ad esempio, le copertine dei libri e le vendite dei libri. Un modello lineare addestrato su valori non elaborati dovrebbe trovare qualcosa sulle copertine dei libri che vendono un milione di copie che sia 10.000 volte più efficace delle copertine dei libri che ne vendono solo 100. Tuttavia, la scalabilità dei dati di log di tutte le cifre di vendita rende l'attività molto più fattibile. Ad esempio, il logaritmo di 100 è:
~4.6 = ln(100)
mentre il logaritmo di 1.000.000 è:
~13.8 = ln(1,000,000)
Quindi, il logaritmo di 1.000.000 è solo circa tre volte più grande del logaritmo di 100. Probabilmente potresti immaginare che la copertina di un best seller sia circa tre volte più efficace (in qualche modo) di quella di un libro che vende poco.
Clip
Il taglio è una tecnica per ridurre al minimo l'influenza di outlier estreme. In breve, il ritaglio solitamente (riduce) il valore dei valori anomali a un valore massimo specifico. Il ritaglio è una un'idea strana, eppure, può essere molto efficace.
Ad esempio, immagina un set di dati contenente una caratteristica denominata roomsPerPerson,
che rappresenta il numero di camere (le stanze totali divise
per numero di occupanti) per le varie abitazioni. Il seguente grafico mostra che oltre il 99% dei valori delle funzionalità è conforme a una distribuzione normale (approssimativamente una media di 1,8 e una deviazione standard di 0,7). Tuttavia, la caratteristica contiene
alcuni outlier, alcuni dei quali estremi:
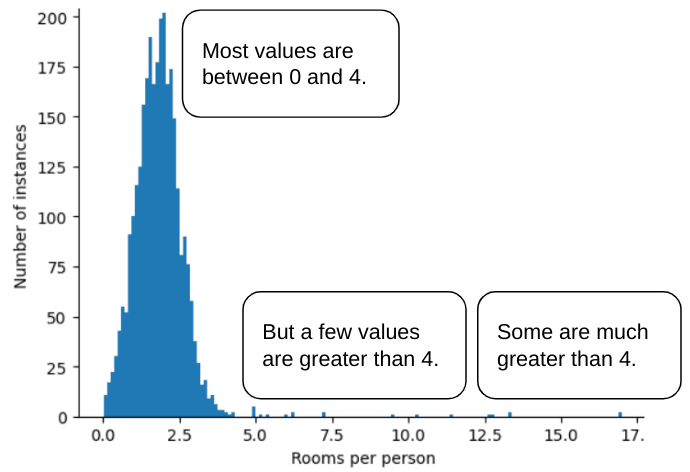
Come si può ridurre al minimo l'influenza di questi outlier estremi? L'istogramma non è una distribuzione uniforme, una distribuzione normale o una distribuzione di legge di potenza. Cosa succede se semplicemente imposti un limite o taglia il valore massimo di
roomsPerPerson a un valore arbitrario, ad esempio 4,0?
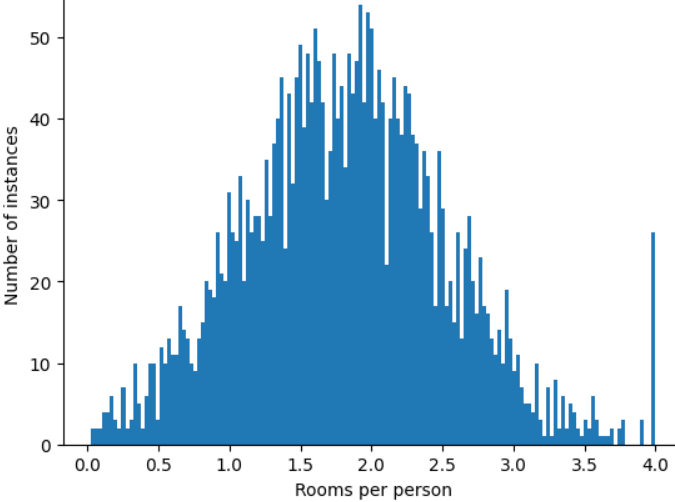
Ritagliare il valore della caratteristica a 4,0 non significa che il modello ignora tutti superiori a 4,0. Piuttosto, significa che tutti i valori maggiori 4.0 ora diventa 4.0. Questo spiega la strana curva a 4,0. Nonostante questo, l'insieme di funzionalità scalate è ora più utile dei dati originali.
Aspetta un attimo. Puoi davvero ridurre ogni valore outlier a un valore arbitrario superiore soglia? Sì, per l'addestramento di un modello.
Puoi anche tagliare i valori dopo aver applicato altre forme di normalizzazione. Ad esempio, supponiamo di utilizzare la scalatura dello z-score, ma alcuni valori anomali hanno valori assoluti molto superiori a 3. In questo caso, potresti:
- Ritaglia i punteggi Z maggiori di 3 per ottenere esattamente 3.
- Taglia i valori Z inferiori a -3 in modo che diventino esattamente -3.
Il ritaglio impedisce al modello di eseguire l'indicizzazione in eccesso su dati non importanti. Tuttavia, alcuni valori anomali sono in realtà importanti, quindi ritaglia i valori con attenzione.
Riepilogo delle tecniche di normalizzazione
| Tecnica di normalizzazione | Formula | Quando utilizzarle |
|---|---|---|
| Scala lineare | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | Quando la funzionalità è distribuita in modo uniforme su un intervallo fisso. |
| Scalabilità punteggio z | $$ x' = \frac{x - μ}{σ}$$ | Quando la distribuzione delle caratteristiche non contiene outlier estremi. |
| Scala logaritmica | $$ x' = log(x)$$ | Quando la funzionalità è conforme alla legge di potenza. |
| Clip | Se $x > max$, imposta $x' = max$ Se $x < min$, imposta $x' = min$ |
Quando la caratteristica contiene anomalie estreme. |
Esercizio: verifica le tue conoscenze
Supponiamo che tu stia sviluppando un modello che prevede la
la produttività in base alla temperatura misurata all'interno del data center.
Quasi tutti i valori temperature nel set di dati rientrano
tra 15 e 30 °C, con le seguenti eccezioni:
- Una o due volte all'anno, in giornate estremamente calde, vengono registrati alcuni valori tra
31 e 45 a
temperature. - Ogni millesimo punto in
temperatureè impostato su 1000 anziché sulla temperatura effettiva.
Quale sarebbe una tecnica di normalizzazione ragionevole per
temperature?
I valori di 1000 sono errori e devono essere eliminati anziché essere tagliati.
I valori compresi tra 31 e 45 sono punti dati legittimi. Il ritaglio potrebbe essere una buona idea per questi valori, supponendo che questo set di dati non contiene abbastanza esempi in questo intervallo di temperature per addestrare il modello per fare previsioni efficaci. Tuttavia, durante l'inferenza, tieni presente che il modello troncato effettuerebbe la stessa previsione per una temperatura di 45 °C e una di 35 °C.