Dane liczbowe: normalizacja

Po zbadaniu danych za pomocą technik statystycznych i wizualizacji należy je przekształcić w sposób, który pozwoli na skuteczniejsze trenowanie modelu. Celem normalizacji jest przekształcenie cech tak, aby były one na podobnej skali. Rozważmy na przykład te 2 funkcje:

• Funkcja X obejmuje zakres od 154 do 24 917 482.
• Funkcja Y ma zakres od 5 do 22.

Te 2 funkcje obejmują bardzo różne zakresy. Normalizacja może zmienić wartości X i Y tak, aby miały podobny zakres, np. od 0 do 1.

Normalizacja zapewnia te korzyści:

• pomaga modelom szybciej się dopasowywać podczas trenowania. Gdy różne cechy mają różne zakresy, metoda gradientu może „odbywać się” i spowolniać konwergencję. Bardziej zaawansowane algorytmy optymalizacyjne, takie jak Adagrad i Adam, zapobiegają temu problemowi, zmieniając skuteczną szybkość uczenia się w czasie.
• Pomaga modelom wyciągać lepsze wnioski. Jeśli różne cechy mają różne zakresy, uzyskany model może generować mniej przydatne prognozy.
• Pomaga uniknąć pułapki typu „NaN”, gdy wartości cech są bardzo wysokie. NaN to skrót od not a number (nie jest liczbą). Gdy wartość w modelu przekracza limit precyzji liczby zmiennoprzecinkowej, system zamiast liczby ustawia wartość NaN. Gdy 1 liczba w modelu stanie się NaN, inne liczby w tym modelu również w końcu staną się NaN.
• Pomaga modelowi uczyć się odpowiednich wag dla każdej cechy. Bez skalowania cech model zwraca zbyt dużą uwagę na cechy o szerokich zakresach i nie wystarczająco dużą na cechy o wąskich zakresach.

Zalecamy normalizowanie cech liczbowych obejmujących wyraźnie różne zakresy (np. wiek i dochody). Zalecamy też znormalizowanie pojedynczej cechy numerycznej, która obejmuje szeroki zakres, takiej jak city population..

Ostrzeżenie: jeśli podczas trenowania normalizujesz cechę, musisz ją też normalizować podczas tworzenia prognoz.

Rozważ te 2 funkcje:

• Najniższa wartość funkcji A to -0,5, a najwyższa to +0,5.
• Najniższa wartość funkcji B to -5,0, a najwyższa – +5,0.

Cechy A i B mają stosunkowo wąskie zakresy. Jednak zakres funkcji B jest 10 razy szerszy niż zakres funkcji A. Dlatego:

• Na początku trenowania model zakłada, że Cecha B jest 10 razy „ważniejsza” niż Cecha A.
• Trening będzie trwał dłużej niż powinien.
• W efekcie model może nie być optymalny.

Ogólne szkody spowodowane brakiem normalizacji będą stosunkowo niewielkie, ale zalecamy normalizację funkcji A i B według tej samej skali, np. od -1,0 do +1,0.

Teraz weź pod uwagę 2 funkcje o większym zakresie:

• Najniższa wartość funkcji C to -1, a najwyższa +1.
• Najniższa wartość funkcji D to +5000, a najwyższa – [phone].

Jeśli nie znormalizujesz atrybutów C i D, Twój model prawdopodobnie nie będzie optymalny. Ponadto trening będzie potrzebował znacznie więcej czasu na zbieżność lub w ogóle nie będzie się zbieży.

W tej sekcji omówiono 3 popularne metody normalizacji:

• skalowanie liniowe
• Skalowanie standaryzacji Z
• skalowanie logarytmiczne

Ta sekcja zawiera również informacje o przycinaniu. Chociaż nie jest to prawdziwa technika normalizacji, przycinanie pozwala uporządkować niesforne cechy liczbowe w zakresy, które dają lepsze modele.

Skala liniowa

Skalowanie liniowe (częściej nazywane po prostu skalowaniem) oznacza konwersję wartości zmiennoprzecinkowych z ich naturalnego zakresu na zakres standardowy, zwykle od 0 do 1 lub od -1 do +1.

Aby zobaczyć obliczenia, kliknij ikonę.

Aby przeskalować dane do zakresu standardowego od 0 do 1, użyj tej formuły:

$$ x' = (x - x_{min}) / (x_{max} - x_{min}) $$

gdzie:

• $x'$ to wartość po skalowaniu.
• $x$ to wartość początkowa.
• $x_{min}$ to najniższa wartość w zbiorze danych tej funkcji.
• $x_{max}$ to najwyższa wartość w zbiorze danych tej cechy.

Weźmy na przykład cechę o nazwie quantity, której naturalny zakres wynosi od 100 do 900. Załóżmy, że naturalna wartość quantity w danym przykładzie to 300. Dlatego wartość 300 możesz obliczyć w ten sposób:

• $x$ = 300
• $x_{min}$ = 100
• $x_{max}$ = 900

x' = (300 - 100) / (900 - 100)
x' = 200 / 800
x' = 0.25

---

Skalowanie liniowe jest dobrym wyborem, gdy są spełnione wszystkie te warunki:

• Dolna i górna granica danych nie zmieniają się znacząco w czasie.
• Funkcja zawiera niewiele lub żadne wartości odstające, które nie są skrajne.
• Cecha jest rozłożona w przybliżeniu równomiernie w całym zakresie. Oznacza to, że histogram będzie zawierał w przybliżeniu równe paski dla większości wartości.

Załóżmy, że człowiek age to funkcja. Skalowanie liniowe to dobra technika normalizacji w przypadku age, ponieważ:

• Przybliżone dolne i górne granice to 0–100.
• Plik age zawiera stosunkowo niewielki odsetek wartości odstających. Tylko około 0,3% ludzi ma więcej niż 100 lat.
• Chociaż niektóre grupy wiekowe są nieco lepiej reprezentowane niż inne, duży zbiór danych powinien zawierać wystarczającą liczbę przykładów dla wszystkich grup wiekowych.

Uwaga: większość funkcji w rzeczywistych zastosowaniach nie spełnia wszystkich kryteriów skalowania liniowego. Skalowanie według wartości z-score jest zwykle lepszym wyborem niż skalowanie liniowe.

Ćwiczenie: sprawdź swoją wiedzę

Załóżmy, że Twój model ma cechę o nazwie net_worth, która zawiera wartość netto różnych osób. Czy skalowanie liniowe byłoby dobrą techniką normalizacji w przypadku net_worth? Dlaczego?

Aby zobaczyć odpowiedź, kliknij ikonę.

Odpowiedź: skalowanie liniowe nie jest dobrym wyborem do normalizacji.net_worth Ta funkcja zawiera wiele wartości odstających, a wartości nie są równomiernie rozłożone w głównym zakresie. Większość osób znalazłaby się w bardzo wąskim paśmie ogólnego zakresu.

---

Skalowanie standaryzacji Z

Wynik testu Z to liczba standardowych odchyleń wartości od średniej. Na przykład wartość, która jest wyższa o 2 odchylenia standardowe od średniej, ma współczynnik Z równy +2,0. Wartość, która jest o 1,5 odchylenia standardowego mniej od średniej, ma współczynnik Z-score równy –1,5.

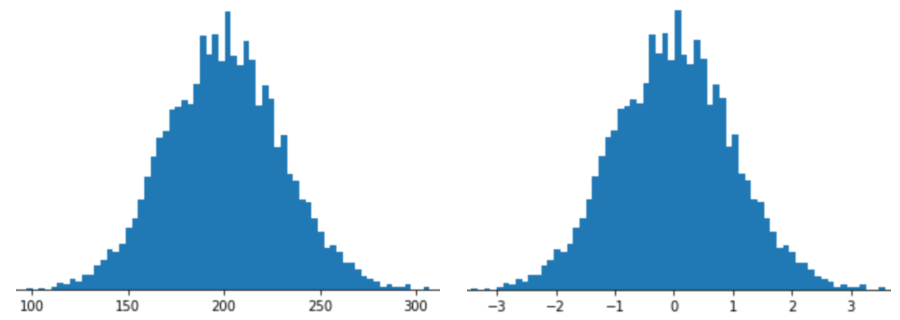
Reprezentowanie cechy za pomocą skalowania na podstawie wyniku Z oznacza przechowywanie w wektorze cech wyniku Z tej cechy. Na przykład na rysunku poniżej widać 2 histogramy:

• Po lewej stronie klasyczny rozkład normalny.
• Po prawej stronie ta sama dystrybucja znormalizowana za pomocą skalowania wartości Z.

Rysunek 4. Dane wyjściowe (po lewej) w porównaniu ze współczynnikiem Z (po prawej) dla rozkładu normalnego.

Skalowanie według wartości z-score jest też dobrym wyborem w przypadku danych takich jak na poniższym rysunku, które mają tylko przybliżoną normalną dystrybucję.

Rysunek 5. Dane wyjściowe (po lewej) w porównaniu ze skalowaniem według wartości Z (po prawej) w przypadku nieklasycznego rozkładu normalnego.

Aby zobaczyć obliczenia, kliknij ikonę.

Aby znormalizować wartość $x$ do wartości Z-score, użyj tej formuły:

$$ x' = (x - μ) / σ $$

gdzie:

• $x'$ to standaryzacja Z.
• $x$ to wartość nieprzetworzona, czyli wartość, którą normalizujesz.
• $μ$ to średnia.
• $σ$ to odchylenie standardowe.

Na przykład:

• mean = 100
• odchylenie standardowe = 20
• wartość początkowa = 130

Dlatego:

  Z-score = (130 - 100) / 20
  Z-score = 30 / 20
  Z-score = +1.5

---

Kliknij ikonę, aby dowiedzieć się więcej o rozkładach normalnych.

W klasycznym rozkładzie normalnym:

• Przynajmniej 68,27% danych ma wynik Z-score w zakresie od -1,0 do +1,0.
• Co najmniej 95,45% danych ma współczynnik Z-score w zakresie od -2,0 do +2,0.
• Co najmniej 99,73% danych ma wynik Z-score w zakresie od -3,0 do +3,0.
• Co najmniej 99,994% danych ma wynik Z-score w zakresie od -4,0 do +4,0.

Punkty danych o wyniku poniżej -4,0 lub powyżej +4,0 są rzadkie, ale czy są one rzeczywiście wartościami odstającemi? Termin wyjątki nie ma ścisłej definicji, więc nikt nie może tego stwierdzić. Pamiętaj, że zbiór danych z wystarczająco dużą liczbą przykładów prawie na pewno będzie zawierać co najmniej kilka takich „rzadkich” przykładów. Na przykład cecha z miliardem przykładów zgodnych z klasycznym rozkładem normalnym może mieć nawet 60 tys. przykładów z wynikiem poza zakresem od -4, 0 do +4,0.

---

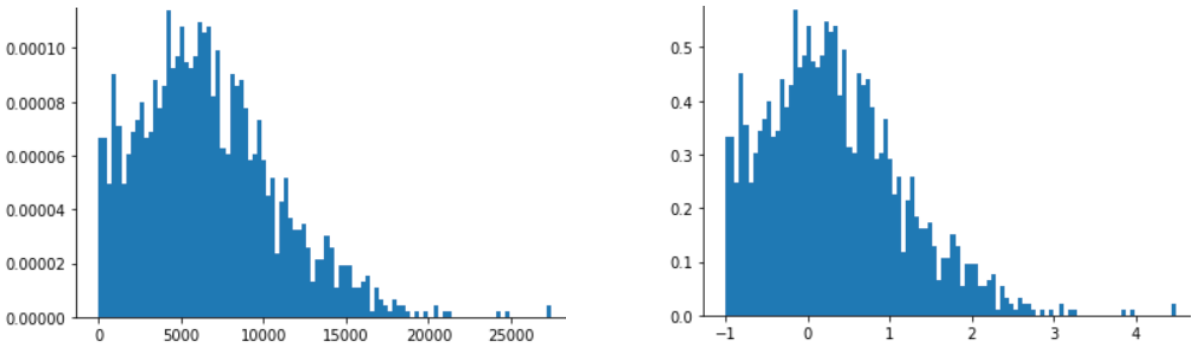
Z-score jest dobrym wyborem, gdy dane mają rozkład normalny lub rozkład podobny do rozkładu normalnego.

Pamiętaj, że niektóre rozkłady mogą być normalne w większości swojego zakresu, ale nadal mogą zawierać wartości skrajne. Na przykład prawie wszystkie punkty cechy net_worth mogą mieścić się w 3 odchyleniach standardowych, ale niektóre przykłady tej cechy mogą znajdować się w setkach odchyleń standardowych od średniej. W takich sytuacjach możesz połączyć skalowanie według wartości Z-score z inną formą normalizacji (zwykle odcięciem) w celu rozwiązania tego problemu.

Ćwiczenie: sprawdź swoją wiedzę

Załóżmy, że Twój model trenuje na podstawie atrybutu o nazwie height, który zawiera dane dotyczące wzrostu 10 milionów dorosłych kobiet. Czy standaryzacja za pomocą Z-score będzie dobrą techniką normalizacji w przypadku height? Dlaczego?

Aby zobaczyć odpowiedź, kliknij ikonę.

Odpowiedź: skalowanie według wartości z testu Z byłoby dobrą techniką normalizacji w przypadku zmiennej height, ponieważ ta zmienna jest zgodna z rozkładem normalnym. 10 milionów przykładów oznacza wiele wartości odstających – prawdopodobnie wystarczająco dużo, aby model mógł nauczyć się wzorów na podstawie bardzo wysokich lub bardzo niskich wartości Z-score.

---

Skalowanie logarytmiczne

Skalibrowanie logarytmiczne oblicza logarytm wartości nieprzetworzonej. Teoretycznie logarytm może mieć dowolną podstawę. W praktyce skalowanie logarytmiczne zwykle oblicza logarytm naturalny (ln).

Aby zobaczyć obliczenia, kliknij ikonę.

Aby znormalizować wartość $x$, użyj tej formuły:

$$ x' = ln(x) $$

gdzie:

• $x'$ to logarytm naturalny z $x$.
• wartość początkowa = 54,598

Dlatego logarytm pierwotnej wartości wynosi około 4, 0:

  4.0 = ln(54.598)

---

Skalowanie logarytmiczne jest przydatne, gdy dane są zgodne z rozkładem mocy. W ogólnym ujęciu rozkład według prawa potęgowego wygląda tak:

• Niskie wartości X mają bardzo wysokie wartości Y.
• Wraz ze wzrostem wartości X wartości Y szybko maleją. W związku z tym wysokie wartości X mają bardzo niskie wartości Y.

Oceny filmów są dobrym przykładem rozkładu według prawa potęgowego. Na poniższym rysunku:

• Kilka filmów ma wiele ocen użytkowników. (niskie wartości atrybutu X mają wysokie wartości atrybutu Y).
• Większość filmów ma bardzo mało ocen użytkowników. (wysokie wartości X mają niskie wartości Y).

Przejście na skalę logarytmiczną zmienia rozkład, co ułatwia wytrenowanie modelu, który będzie lepiej prognozował.

Rysunek 6. Porównanie rozkładu nieprzetworzonego z jego logiem.

Drugi przykład: sprzedaż książek podlega rozkładowi według prawa potęgowego, ponieważ:

• Większość opublikowanych książek sprzedaje się w bardzo niewielkiej liczbie egzemplarzy, może 100–200.
• Niektóre książki sprzedają się w umiarkowanej liczbie, w tysiącach egzemplarzy.
• Tylko kilka najlepiej sprzedających się tytułów osiągnie sprzedaż ponad miliona egzemplarzy.

Załóżmy, że trenujesz model liniowy, aby znaleźć zależność między okładkami książek a ich sprzedażą. Model liniowy trenowany na podstawie wartości nieprzetworzonych musiałby znaleźć coś w okładkach książek, które sprzedały milion egzemplarzy, co jest 10 tysięcy razy bardziej skuteczne niż okładki książek, które sprzedały tylko 100 egzemplarzy. Jednak dzięki skalowaniu wszystkich danych o sprzedaży zadanie to staje się znacznie łatwiejsze do wykonania. Na przykład logarytm z 100 to:

  ~4.6 = ln(100)

natomiast dziennik o długości 1 000 000 znaków:

  ~13.8 = ln(1,000,000)

Zatem log 1 000 000 jest tylko około 3 razy większy niż log 100. Prawdopodobnie możesz sobie wyobrazić, że okładka bestsellera jest około trzykrotnie bardziej atrakcyjna (w jakimś sensie) niż okładka książki, która nie cieszy się zbytnim powodzeniem.

Przycinanie

Odcięcie wartości odstających to technika minimalizowania wpływu wartości skrajnych. Krótko mówiąc, przycinanie zwykle ogranicza (zmniejsza) wartość wartości odstających do określonej wartości maksymalnej. Clipping to dziwna koncepcja, ale może być bardzo skuteczna.

Wyobraź sobie na przykład zbiór danych zawierający cechę o nazwie roomsPerPerson, która reprezentuje liczbę pokoi (łączna liczba pokoi podzielona przez liczbę osób) w różnych domach. Na poniższym wykresie widać, że ponad 99% wartości funkcji jest zgodne z rozkładem normalnym (średnia 1,8 i odchylenie standardowe 0,7). Funkcja zawiera jednak kilka wartości odstających, niektóre z nich są bardzo duże:

Rysunek 7. głównie normalne, ale nie do końca normalne.

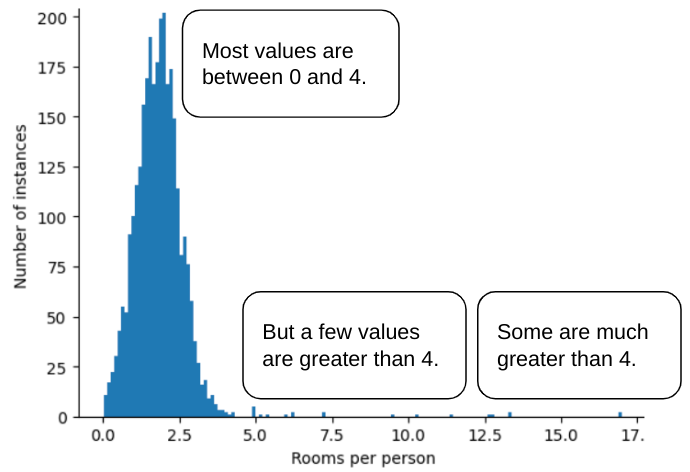
Jak można zminimalizować wpływ tych skrajnych wartości? Widok histogramu nie przypomina rozkładu równomiernego, normalnego ani rozkładu według prawa potęgowego. Co się stanie, jeśli po prostu ograniczysz lub obrzeżysz maksymalną wartość funkcji roomsPerPerson do dowolnej wartości, np.4,0?

Rysunek 8. Obcinanie wartości cech przy wartości 4,0.

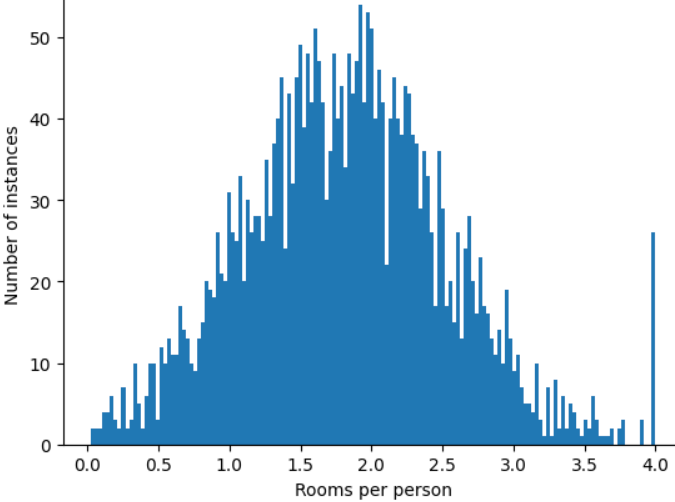
Ograniczenie wartości funkcji na poziomie 4,0 nie oznacza, że model ignoruje wszystkie wartości większe niż 4,0. Oznacza to, że wszystkie wartości większe niż 4,0 są teraz ustawiane na 4,0. To wyjaśnia dziwny szczyt w 4.0. Pomimo tego wzgórza skalowany zestaw funkcji jest teraz bardziej przydatny niż pierwotne dane.

Zaczekaj chwilę. Czy naprawdę możesz zredukować wszystkie wartości odstające do dowolnego górnego progu? Podczas trenowania modelu.

Wartości możesz też przyciąć po zastosowaniu innych form normalizacji. Załóżmy na przykład, że używasz skalowania na podstawie wartości z tabeli Z, ale kilka wartości odstających ma wartości bezwzględne znacznie większe niż 3. W takim przypadku możesz:

• Zredukuj wartości Z-score większe niż 3, aby były dokładnie równe 3.
• Zredukuj wartości poniżej -3, tak aby wynosiły dokładnie -3.

Dzięki temu model nie będzie nadmiernie indeksować nieistotnych danych. Niektóre wartości odstające są jednak ważne, dlatego należy ostrożnie podchodzić do ich przycinania.

Podsumowanie metod normalizacji

Najlepsza technika normalizacji to ta, która sprawdza się w praktyce. Jeśli więc uważasz, że nowe pomysły będą dobrze działać w przypadku rozkładu cech, wypróbuj je.

Technika normalizacji	Formuła	Kiedy używać
Skala liniowa	$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$	Gdy funkcja jest równomiernie rozłożona w ramach stałego zakresu.
Skalowanie standaryzacji Z	$$ x' = \frac{x - μ}{σ}$$	Gdy rozkład funkcji nie zawiera skrajnych wartości odstających.
Skalowanie logarytmiczne	$$ x' = log(x)$$	gdy funkcja jest zgodna z zasadami prawa potęgi.
Przycinanie	Jeśli $x > max$, ustaw $x' = max$ Jeśli $x < min$, ustaw $x' = min$	gdy funkcja zawiera skrajne wartości odstające.

Ćwiczenie: sprawdzenie wiedzy

Która technika najlepiej nadaje się do normalizacji atrybutu o takim rozkładzie?

Skalowanie standaryzacji Z

Punkty danych zwykle odpowiadają rozkładowi normalnemu, więc skalowanie według wartości Z spowoduje, że znajdą się one w zakresie od –3 do +3.

Skala liniowa

Zapoznaj się z dyskusją na temat technik normalizacji na tej stronie i spróbuj ponownie.

Skalowanie logarytmiczne

Zapoznaj się z dyskusją na temat technik normalizacji na tej stronie i spróbuj ponownie.

Przycinanie

Zapoznaj się z dyskusjami na temat technik normalizacji na tej stronie i spróbuj ponownie.

Załóżmy, że opracowujesz model, który przewiduje wydajność centrum danych na podstawie temperatury zmierzonej wewnątrz tego centrum. Prawie wszystkie wartości temperature w Twoim zbiorze danych mieszczą się w zakresie 15–30 °C, z tymi wyjątkami:

• Raz lub dwa razy w roku, w bardzo gorące dni, w temperature rejestruje się kilka wartości z zakresu 31–45.
• Każdy tysiąc punktów w pliku temperature ma wartość 1000, a nie rzeczywistą temperaturę.

Która z tych technik normalizacji byłaby odpowiednia w przypadku temperature?

Wytnij wartości wartości odstające z zakresu 31–45, ale usuń wartości odstające o wartość 1000

Wartości 1000 są błędne i należy je usunąć, a nie przyciąć.

Wartości od 31 do 45 są prawidłowymi punktami danych. W przypadku tych wartości warto zastosować przycinanie, jeśli zbiór danych nie zawiera wystarczającej liczby przykładów w danym zakresie temperatury, aby można było wytrenować model w celu uzyskania dobrych prognoz. Podczas wnioskowania należy jednak pamiętać, że przycięty model będzie przewidywać tę samą temperaturę dla temperatury 45 °C i 35 °C.

Wycięcie wszystkich wartości odstających

Zapoznaj się z dyskusjami na temat technik normalizacji na tej stronie i spróbuj ponownie.

Usuń wszystkie wartości odstające

Zapoznaj się z dyskusjami na temat technik normalizacji na tej stronie i spróbuj ponownie.

Usuń wartości odstające z zakresu 31–45, ale przytnij wartości odstające o wartość 1000.

Zapoznaj się z dyskusją na temat technik normalizacji na tej stronie i spróbuj ponownie.

Kluczowe terminy:

• Przycinanie
• Pułapka NaN
• Normalizacja
• Skalowanie
• Normalizacja z wykorzystaniem standaryzacji Z