Числові дані: нормалізація

Після вивчення даних за допомогою статистичних методів і методів візуалізації слід трансформувати їх так, щоб ваша модель навчалась ефективніше. Мета нормалізації – трансформувати ознаки так, щоб вони мали подібний масштаб. Наприклад, розгляньмо дві ознаки, наведені нижче.

• Ознака X охоплює діапазон від 154 до 24 917 482.
• Ознака Y – від 5 до 22.

Діапазони значень цих двох ознак дуже різні. Нормалізація може обробити X і Y так, щоб ці діапазони були подібні, наприклад, від 0 до 1.

Нижче перелічено переваги нормалізації.

• Допомагає моделям швидше збігатися під час навчання. Коли ознаки мають різні діапазони, градієнтний спуск може "скакати" й сповільнювати збіжність. Новітні оптимізатори, як-от Adagrad і Adam захищають від цієї проблеми, змінюючи ефективну швидкість навчання із часом.
• Допомагає моделям робити кращі прогнози. Якщо ознаки мають різні діапазони, отримана модель може давати менш корисні прогнози.
• Допомагає уникнути "пастки NaN", коли значення ознак дуже великі. NaN – це абревіатура, яка означає не число. Коли певне значення в моделі перевищує обмеження точності з рухомою комою, система змінює це число на NaN. Коли одне число в моделі змінюється на NaN, інші також із часом стають такими.
• Допомагає моделі вивчити відповідні значення ваги для кожної ознаки. Без масштабування ознак модель приділяє забагато уваги ознакам із широкими діапазонами й недостатньо тим, які мають вузькі діапазони.

Рекомендуємо нормалізувати числові ознаки, у яких абсолютно різні діапазони (наприклад, вік і дохід). Також рекомендуємо нормалізувати одну числову ознаку, діапазон якої широкий, наприклад city population. (населення міста).

Увага: якщо ви нормалізували ознаку під час навчання, її також потрібно нормалізувати під час прогнозування.

Розгляньмо дві ознаки, наведені нижче.

• Найменше значення ознаки A становить –0,5, а найвище дорівнює +0,5.
• Найменше значення ознаки B становить –5,0, а найвище дорівнює +5,0.

Ознака A і ознака B мають відносно вузьку ширину діапазону. Однак діапазон ознаки B в 10 разів ширший за діапазон ознаки A. Тому:

• на початку навчання модель припускає, що ознака B в десять разів "важливіша", ніж A;
• навчання займе більше часу, ніж мало б;
• отримана модель може бути субоптимальною.

Загальна шкода через відсутність нормалізації буде відносно невеликою; однак ми все одно рекомендуємо нормалізувати ознаки A і B до однакового масштабу (наприклад, діапазону від –1,0 до +1,0).

Тепер розгляньмо дві ознаки, які мають більшу невідповідність діапазонів.

• Найменше значення ознаки C становить –1, а найвище дорівнює +1.
• Найменше значення ознаки D становить +5000, а найвище дорівнює [phone].

Якщо ви не нормалізуєте ознаки C й D, ваша модель, найімовірніше, буде субоптимальною. Крім того, модель досягне збіжності тільки після значно довшого навчання або їй не вдасться цього зробити взагалі.

У цьому розділі розглядаються три популярні методи нормалізації:

• лінійне масштабування;
• масштабування значення Z;
• логарифмічне масштабування.

Крім того, тут пояснюється поняття обрізання. Хоча обрізання не є фактичним методом нормалізації, воно допомагає нормалізувати неконтрольовані числові ознаки в діапазони, на основі яких створюються кращі моделі.

Лінійне масштабування

Лінійне масштабування (частіше скорочено – масштабування) означає перетворення значень із рухомою комою з їх звичайного діапазону в стандартний (типові – від 0 до 1 або від –1 до +1).

Натисніть значок, щоб побачити математичне підґрунтя.

Використовуйте формулу, наведену нижче, щоб масштабувати дані до стандартного діапазону від 0 до 1 включно:

$$ x' = (x - x_{min}) / (x_{max} - x_{min}) $$

Визначення змінних:

• $x'$ – масштабоване значення;
• $x$ – початкове значення;
• $x_{min}$ – найменше значення з набору даних цієї ознаки;
• $x_{max}$ – найбільше значення з набору даних цієї ознаки.

Наприклад, розгляньмо ознаку quantity (кількість), звичайний діапазон якої – від 100 до 900. Припустімо, що звичайне значення quantity в конкретному прикладі дорівнює 300. Нормалізоване значення 300 можна обчислити так:

• $x$ = 300
• $x_{min}$ = 100
• $x_{max}$ = 900

x' = (300 - 100) / (900 - 100)
x' = 200 / 800
x' = 0.25

---

Лінійне масштабування – гарний вибір, якщо виконуються всі умови, наведені нижче.

• Нижня й верхня межі даних не дуже змінюються із часом.
• Ознака містить небагато викидів або їх немає взагалі, і вони не екстремальні.
• Ознака приблизно рівномірно розподілена по всьому діапазону, тобто гістограма показала б приблизно однакові стовпчики для більшості значень.

Припустімо, що ознакою є age (вік людини). Лінійне масштабування – гарний метод нормалізації age із причин, наведених нижче.

• Приблизні нижня й верхня межі становлять від 0 до 100.
• Ознака age має відносно невеликий відсоток викидів. Вік лише близько 0,3% населення більший за 100 років.
• Хоча певні вікові групи представлено дещо краще, ніж інші, великий набір даних має містити достатню кількість прикладів для всіх вікових груп.

Примітка. Більшість реальних ознак не відповідають усім критеріям лінійного масштабування. Кращим методом нормалізації, ніж лінійне масштабування, зазвичай є масштабування значення Z.

Вправа. Перевірте свої знання

Припустімо, що ваша модель має ознаку net_worth (чистий капітал різних людей). Чи буде лінійне масштабування гарним методом нормалізації для ознаки net_worth? Чому?

Натисніть значок, щоб побачити відповідь.

Відповідь. Лінійне масштабування – поганий вибір для нормалізації net_worth. Ця ознака має багато викидів, а значення нерівномірно розподілені в первинному діапазоні. Більшість людей представляла б дуже вузька смуга загального діапазону.

---

Масштабування значення Z

Значення Z – це кількість стандартних відхилень, на які число більше чи менше за середнє значення. Наприклад, число, яке на 2 стандартні відхилення більше за середнє, має значення Z +2,0. Число, яке на 1,5 стандартного відхилення менше за середнє, має значення Z –1,5.

Представити ознаку за допомогою масштабування значення Z – це зберегти її значення Z у векторі ознак. Наприклад, на наступному рисунку показано дві гістограми:

• ліворуч – класичний нормальний розподіл;
• праворуч – той самий розподіл, нормалізований за допомогою масштабування значення Z.

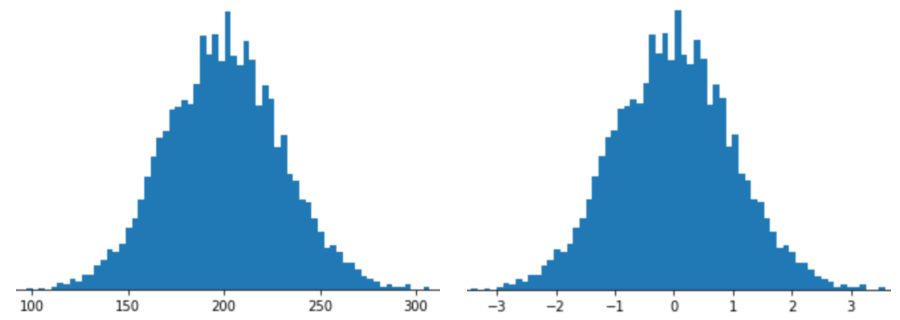
Рисунок 4. Дані з нормальним розподілом: необроблені (ліворуч) і нормалізовані за допомогою масштабування значення Z (праворуч).

Масштабування значення Z – це також гарний вибір для даних, подібних до показаних на наступному рисунку, які мають лише приблизно нормальний розподіл.

Рисунок 5. Дані з некласичним нормальним розподілом: необроблені (ліворуч) і нормалізовані за допомогою масштабування значення Z (праворуч).

Натисніть значок, щоб побачити математичне підґрунтя.

Використовуйте формулу, наведену нижче, щоб нормалізувати $x$ до значення Z:

$$ x' = (x - μ) / σ $$

Визначення змінних:

• $x'$ – значення Z;
• $x$ – необроблене значення (тобто $x$ – це число, яке нормалізується);
• $μ$ – середнє значення;
• $σ$ – стандартне відхилення.

Припустімо, що:

• середнє значення становить 100;
• стандартне відхилення дорівнює 20;
• первинне значення становить 130.

Тоді:

  Z-score = (130 - 100) / 20
  Z-score = 30 / 20
  Z-score = +1.5

---

Натисніть значок, щоб дізнатися більше про нормальні розподіли.

У класичному нормальному розподілі:

• принаймні 68,27% даних мають значення Z від –1,0 до +1,0;
• принаймні 95,45% даних мають значення Z від –2,0 до +2,0;
• принаймні 99,73% даних мають значення Z від –3,0 до +3,0;
• принаймні 99,994% даних мають значення Z від –4,0 до +4,0.

Тому точки даних зі значенням Z менше ніж –4,0 або більше ніж +4,0 зустрічаються рідко. Але чи справді вони є викидами? Оскільки поняття викиди не має чіткого визначення, не можна сказати напевно. Зауважте, що набір даних із достатньо великою кількістю прикладів майже напевно міститиме принаймні кілька таких "рідкісних" прикладів. Наприклад, якщо ознака з класичним нормальним розподілом має один мільярд прикладів, значення до 60 000 із них можуть виходити за межі діапазону від –4,0 до +4,0.

---

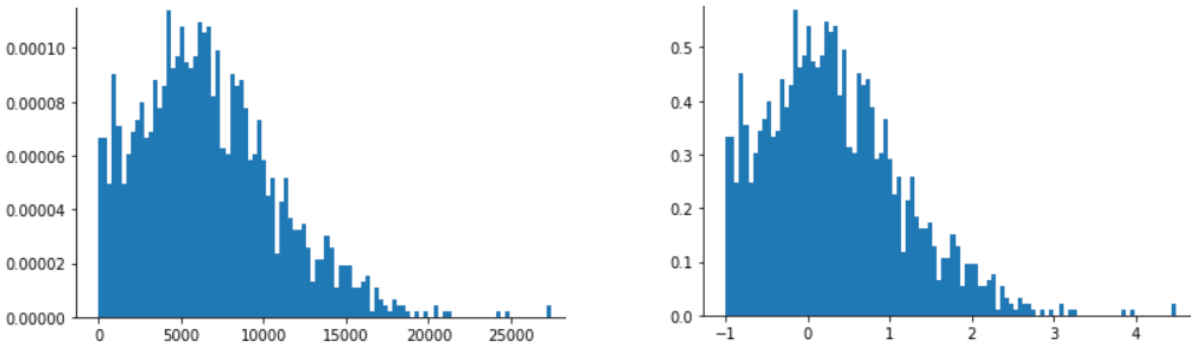
Значення Z – гарний вибір, якщо дані відповідають нормальному розподілу або схожому на нього.

Зауважте, що іноді більшість даних діапазону відповідає нормальному розподілу, але є екстремальні викиди. Наприклад, майже всі точки ознаки net_worth можуть бути в межах трьох стандартних відхилень, але кілька її прикладів будуть відрізнятися від середнього значення на сотні стандартних відхилень. У такому разі можна поєднати масштабування значення Z з іншим видом нормалізації (зазвичай це обрізання).

Вправа. Перевірте свої знання

Припустімо, що ваша модель навчається на ознаці height (зріст), яка містить дані десяти мільйонів жінок. Чи буде масштабування значення Z гарним методом нормалізації для height? Чому?

Натисніть значок, щоб побачити відповідь.

Відповідь. Масштабування значення Z – гарний метод нормалізації height, оскільки ця ознака відповідає нормальному розподілу. Серед десяти мільйонів прикладів буде багато викидів. Імовірно, їх достатньо, щоб модель могла вивчити шаблони на дуже великих або малих значеннях Z.

---

Логарифмічне масштабування

У логарифмічному масштабуванні обчислюється логарифм необробленого значення. Теоретично логарифм може мати будь-яку основу; на практиці логарифмічне масштабування зазвичай обчислює натуральний логарифм (ln).

Натисніть значок, щоб побачити математичне підґрунтя.

Використовуйте формулу, наведену нижче, щоб нормалізувати значення $x$ до його логарифма:

$$ x' = ln(x) $$

Визначення змінних:

• $x'$ – натуральний логарифм $x$;
• первинне значення становить 54,598.

Отже, логарифм первинного значення становить приблизно 4,0:

  4.0 = ln(54.598)

---

Логарифмічне масштабування корисне, якщо дані відповідають степеневому розподілу. Умовно кажучи, степеневий розподіл можна описати так:

• малим значенням X відповідають дуже великі значення Y;
• якщо значення X зростають, значення Y швидко зменшуються, тому великим значенням X відповідають дуже малі значення Y.

Хорошим прикладом степеневого розподілу є рейтинги фільмів. Розгляньте рисунок, наведений нижче, і зверніть увагу на таке:

• кілька фільмів мають багато оцінок користувачів (малим значенням X відповідають великі значення Y);
• більшість фільмів мають дуже мало оцінок користувачів (великим значенням X відповідають малі значення Y).

Логарифмічне масштабування змінює цей розподіл, що допомагає навчити модель, яка даватиме кращі прогнози.

Рисунок 6. Порівняння необробленого розподілу з нормалізованим за допомогою логарифмічного масштабування.

Розгляньмо другий приклад. Дані про продаж книг відповідають степеневому розподілу з причин, наведених нижче.

• Найчастіше продається невеликий тираж виданої книги (одна чи дві сотні екземплярів).
• Іноді продається помірний тираж (тисячі екземплярів).
• Лише деякі бестселери розійдуться тиражем понад мільйон екземплярів.

Припустімо, що ви навчаєте лінійну модель, щоб знайти зв’язок, наприклад, між продажами книг і їх обкладинками. Лінійна модель, яка навчається на необроблених значеннях, мала б знайти певні особливості обкладинок бестселерів, які мають у 10 000 разів більший вплив, ніж особливості обкладинок книг, що продаються тиражем лише 100 примірників. Однак завдання стає значно здійсненнішим, якщо нормалізувати всі показники продажів за допомогою логарифмічного масштабування. Наприклад, логарифм 100 становить:

  ~4.6 = ln(100)

А ось логарифм 1 000 000:

  ~13.8 = ln(1,000,000)

Отже, логарифм 1 000 000 лише приблизно втричі більший, ніж логарифм 100. Мабуть, можна уявити собі обкладинку бестселера, яка має приблизно в три рази більший вплив (у певному сенсі), ніж обкладинка книги, що продається малим тиражем.

Обрізання

Обрізання – це метод мінімізації впливу екстремальних викидів. Якщо коротко, обрізання зазвичай обмежує (зменшує) значення викидів до певного максимального значення. Ця ідея здається дивною, однак може бути дуже ефективною.

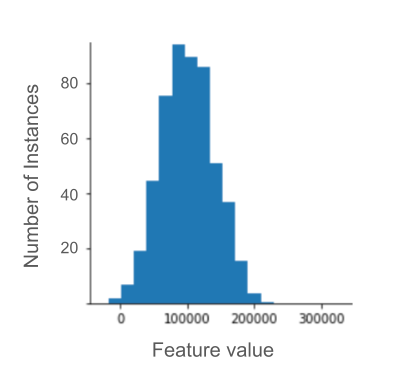
Наприклад, уявіть набір даних про будинки, що містить ознаку roomsPerPerson (загальна кількість кімнат, поділена на кількість мешканців). Як видно з графіка нижче, понад 99% значень ознак відповідають нормальному розподілу (середнє значення й стандартне відхилення становлять приблизно 1,8 і 0,7). Проте ця ознака має кілька викидів, і деякі з них екстремальні.

Рисунок 7. Переважно нормальний розподіл, але не повністю.

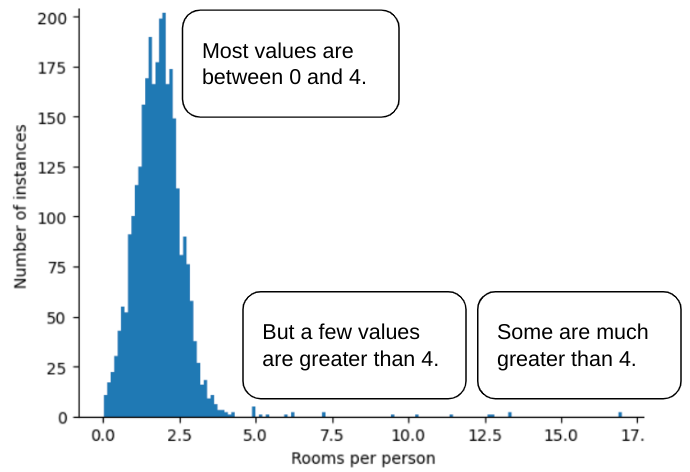
Як можна звести до мінімуму вплив цих екстремальних викидів? Що ж, розподіл, показаний на цій гістограмі, не рівномірний, нормальний чи степеневий. Що як просто обмежити чи обрізати максимальне значення roomsPerPerson до довільного числа (наприклад, 4,0)?

Рисунок 8. Обрізання значень ознак на рівні координати 4,0.

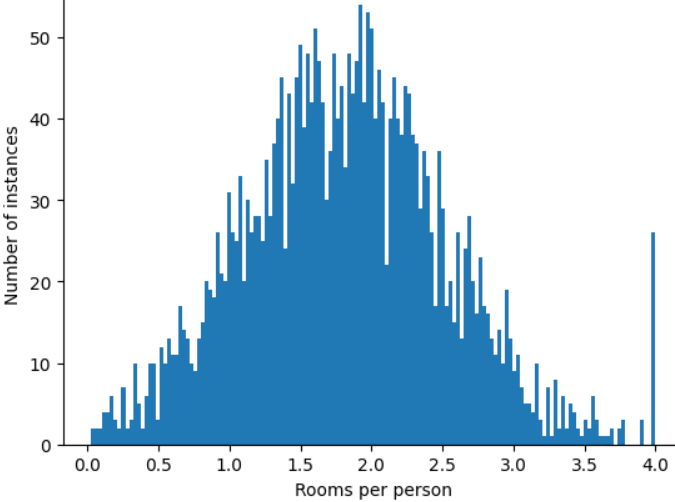
Обрізання значень ознак на рівні координати 4,0 не призведе до того, що модель ігноруватиме всі числа, більші за 4,0. А радше до того, що всі значення, які були більші за 4,0, дорівнюватимуть цьому числу. Саме тому незвично багато значень мають координату 4,0. Попри це, масштабований набір ознак тепер корисніший, ніж первинні дані.

Зачекайте! Справді можна зменшити кожне викидне значення до якогось довільного верхнього порогу? Під час навчання моделі – так.

Ви також можете обрізати значення після застосування інших форм нормалізації. Наприклад, припустімо, що ви використовуєте масштабування значення Z, але абсолютні значення кількох викидів набагато більші за 3. У цьому разі можна:

• обрізати значення Z, більші за 3, щоб вони дорівнювали цьому числу;
• обрізати значення Z, менші за –3, щоб вони дорівнювали цьому числу.

Завдяки обрізанню модель не індексуватиме надмірно неважливі дані. Однак деякі викиди насправді важливі, тому слід обрізати значення обережно.

Короткий опис методів нормалізації

Найкращий метод нормалізації – той, який добре працює на конкретних даних, тому пробуйте нові способи, якщо вважаєте, що вони добре підійдуть для вашого розподілу ознак.

Метод нормалізації	Формула	Коли використовувати
Лінійне масштабування	$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$	Коли ознаку рівномірно розподілено у фіксованому діапазоні.
Масштабування значення Z	$$ x' = \frac{x - μ}{σ}$$	Коли в розподілі ознак немає екстремальних викидів.
Логарифмічне масштабування	$$ x' = log(x)$$	Коли ознака відповідає степеневому розподілу.
Обрізання	Якщо $x > max$, нехай $x' = max$ Якщо $x < min$, нехай $x' = min$	Коли ознака має екстремальні викиди.

Вправа: перевірте свої знання

Який метод буде найпридатнішим для нормалізації ознаки з таким розподілом?

Масштабування значення Z

Точки даних загалом відповідають нормальному розподілу, тому масштабування значення Z трансформує їх у діапазон від –3 до +3.

Лінійне масштабування

Перегляньте пояснення методів нормалізації, наведене на цій сторінці, і повторіть спробу.

Логарифмічне масштабування

Перегляньте пояснення методів нормалізації, наведене на цій сторінці, і повторіть спробу.

Обрізання

Перегляньте пояснення методів нормалізації, наведене на цій сторінці, і повторіть спробу.

Припустімо, ви розробляєте модель, яка прогнозує продуктивність центру обробки даних на основі температури, виміряної всередині нього. Майже всі значення ознаки temperature (температура) з вашого набору даних становлять від 15 до 30 (градусів за Цельсієм), крім винятків, наведених нижче.

• Один-два рази на рік, у надзвичайно спекотні дні, для ознаки temperature реєструється кілька значень від 31 до 45.
• Кожна 1000-на точка ознаки temperature дорівнює 1000, а не значенню фактичної температури.

Який метод нормалізації підійде для temperature?

Обрізати значення викидів із діапазону 31–45, але видалити викиди зі значенням 1000.

Значення 1000 помилкові, тому їх слід видалити, а не обрізати.

Значення з діапазону 31–45 – допустимі точки даних. Обрізання цих значень може бути гарним методом, якщо припустити, що набір даних не містить достатньо прикладів із цього діапазону температур, щоб модель навчилася робити хороші прогнози. Однак зверніть увагу, що при виведенні результатів обрізана модель даватиме однаковий прогноз для температури 45 і 35 градусів.

Обрізати всі викиди

Перегляньте пояснення методів нормалізації, наведене на цій сторінці, і повторіть спробу.

Видалити всі викиди

Перегляньте пояснення методів нормалізації, наведене на цій сторінці, і повторіть спробу.

Видалити викиди з діапазону 31–45, але обрізати викиди зі значенням 1000.

Перегляньте пояснення методів нормалізації, наведене на цій сторінці, і повторіть спробу.

Ключові терміни

• Обрізання
• "Пастка NaN"
• Нормалізація
• Масштабування
• Нормалізація значення Z