پس از بررسی داده های خود از طریق تکنیک های آماری و تجسمی، باید داده های خود را به روش هایی تغییر دهید که به آموزش موثرتر مدل شما کمک کند. هدف نرمال سازی تبدیل ویژگی ها به یک مقیاس مشابه است. به عنوان مثال، دو ویژگی زیر را در نظر بگیرید:
- ویژگی
Xمحدوده 154 تا 24917482 را در بر می گیرد. - ویژگی
Yبین 5 تا 22 را در بر می گیرد.
این دو ویژگی محدوده های بسیار متفاوتی را در بر می گیرند. عادی سازی ممکن است X و Y را طوری دستکاری کند که محدوده مشابهی را در بر گیرند، شاید 0 تا 1.
عادی سازی مزایای زیر را ارائه می دهد:
- کمک می کند تا مدل ها در طول آموزش سریعتر همگرا شوند . هنگامی که ویژگیهای مختلف دامنههای متفاوتی دارند، نزول گرادیان میتواند "جهش" و همگرایی کند شود. گفته می شود، بهینه سازهای پیشرفته تری مانند Adagrad و Adam با تغییر نرخ موثر یادگیری در طول زمان در برابر این مشکل محافظت می کنند.
- به مدل ها کمک می کند تا پیش بینی های بهتری را استنباط کنند . وقتی ویژگیهای مختلف دامنههای متفاوتی دارند، مدل به دست آمده ممکن است پیشبینیهای کمتر مفیدی انجام دهد.
- هنگامی که مقادیر ویژگی بسیار بالا هستند ، از "تله NaN" جلوگیری می کند. NaN مخفف نه عدد است. هنگامی که یک مقدار در یک مدل از حد دقت ممیز شناور فراتر رود، سیستم به جای عدد، مقدار را روی
NaNتنظیم می کند. هنگامی که یک عدد در مدل به NaN تبدیل می شود، اعداد دیگر در مدل نیز در نهایت به NaN تبدیل می شوند. - به مدل کمک می کند تا وزن های مناسب برای هر ویژگی را یاد بگیرد . بدون مقیاسبندی ویژگی، مدل به ویژگیهایی با دامنه وسیع توجه زیادی میکند و به ویژگیهایی با محدوده باریک توجه کافی نمیکند.
توصیه میکنیم ویژگیهای عددی را عادی کنید که محدودههای کاملاً متفاوتی را پوشش میدهند (به عنوان مثال، سن و درآمد). ما همچنین توصیه میکنیم یک ویژگی عددی واحد را که طیف وسیعی از جمله city population.
دو ویژگی زیر را در نظر بگیرید:
- کمترین مقدار ویژگی
A0.5- و بیشترین مقدار 0.5+ است. - کمترین مقدار ویژگی
B-5.0 و بالاترین +5.0 است.
ویژگی A و ویژگی B دهانه های نسبتاً باریکی دارند. با این حال، دهانه ویژگی B 10 برابر بیشتر از دهانه ویژگی A است. بنابراین:
- در شروع آموزش، مدل فرض میکند که ویژگی
Bده برابر «مهمتر» از ویژگیAاست. - آموزش بیش از آنچه باید طول بکشد.
- مدل حاصل ممکن است کمتر از حد بهینه باشد.
آسیب کلی ناشی از عادی نشدن نسبتاً کوچک خواهد بود. با این حال، ما همچنان توصیه می کنیم که ویژگی A و ویژگی B را در مقیاس یکسان، شاید -1.0 تا +1.0 عادی کنید.
اکنون دو ویژگی را با اختلاف دامنه بیشتر در نظر بگیرید:
- کمترین مقدار ویژگی
C-1 و بیشترین مقدار 1+ است. - کمترین مقدار ویژگی
D+5000 و بالاترین +1,000,000,000 است.
اگر ویژگی C و ویژگی D را عادی نکنید، مدل شما احتمالاً کمتر از حد مطلوب خواهد بود. علاوه بر این، آموزش خیلی بیشتر طول می کشد تا همگرا شوند یا حتی نتوانند به طور کامل همگرا شوند!
این بخش سه روش عادی سازی رایج را پوشش می دهد:
- مقیاس بندی خطی
- مقیاس بندی Z-score
- مقیاس بندی ورود به سیستم
این بخش علاوه بر این برش را پوشش می دهد. اگرچه یک تکنیک عادی سازی واقعی نیست، اما برش ویژگی های عددی سرکش را در محدوده هایی که مدل های بهتری تولید می کنند رام می کند.
مقیاس بندی خطی
مقیاسبندی خطی (که معمولاً به صرف مقیاسگذاری کوتاه میشود) به معنای تبدیل مقادیر ممیز شناور از محدوده طبیعی آنها به یک محدوده استاندارد است - معمولاً 0 تا 1 یا -1 به +1.
مقیاس خطی انتخاب خوبی است زمانی که تمام شرایط زیر برآورده شود:
- مرزهای پایین و بالای داده های شما در طول زمان تغییر چندانی نمی کند.
- این ویژگی حاوی مقادیر کمی است یا اصلاً وجود ندارد، و آن نقاط پرت شدید نیستند.
- این ویژگی تقریباً به طور یکنواخت در محدوده آن توزیع شده است. به این معنا که یک هیستوگرام تقریباً میله های یکنواخت را برای اکثر مقادیر نشان می دهد.
فرض کنید age انسان یک ویژگی است. مقیاس بندی خطی یک تکنیک نرمال سازی خوب برای age است زیرا:
- کران پایین و بالایی تقریبی 0 تا 100 است.
-
ageشامل درصد نسبتا کمی از نقاط پرت است. تنها حدود 0.3 درصد از جمعیت بالای 100 سال هستند. - اگرچه سنین خاص تا حدودی بهتر از سایرین نمایش داده می شوند، یک مجموعه داده بزرگ باید شامل نمونه های کافی از همه سنین باشد.
تمرین: درک خود را بررسی کنید
فرض کنید مدل شما دارای ویژگی به نامnet_worth است که دارایی خالص افراد مختلف را در خود جای داده است. آیا مقیاس خطی یک تکنیک عادی سازی خوب برای net_worth خواهد بود؟ چرا یا چرا نه؟ مقیاس بندی Z-score
Z-score تعداد انحرافات استاندارد یک مقدار از میانگین است. به عنوان مثال، مقداری که 2 انحراف استاندارد بیشتر از میانگین است دارای امتیاز Z 2.0+ است. مقداری که 1.5 انحراف استاندارد کمتر از میانگین است دارای امتیاز Z -1.5 است.
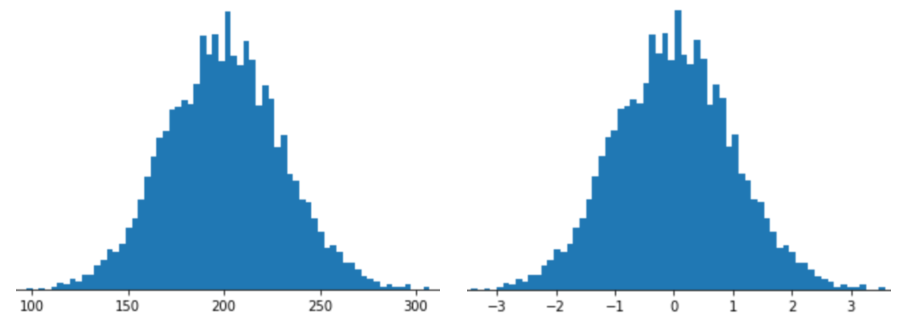
نمایش یک ویژگی با مقیاس بندی Z-score به معنای ذخیره امتیاز Z آن ویژگی در بردار ویژگی است. به عنوان مثال، شکل زیر دو هیستوگرام را نشان می دهد:
- در سمت چپ، یک توزیع نرمال کلاسیک.
- در سمت راست، همان توزیع با مقیاس بندی Z-score نرمال شد.
مقیاس بندی Z-score نیز برای داده هایی مانند آنچه در شکل زیر نشان داده شده است، که فقط توزیع نرمال مبهمی دارد، انتخاب خوبی است.
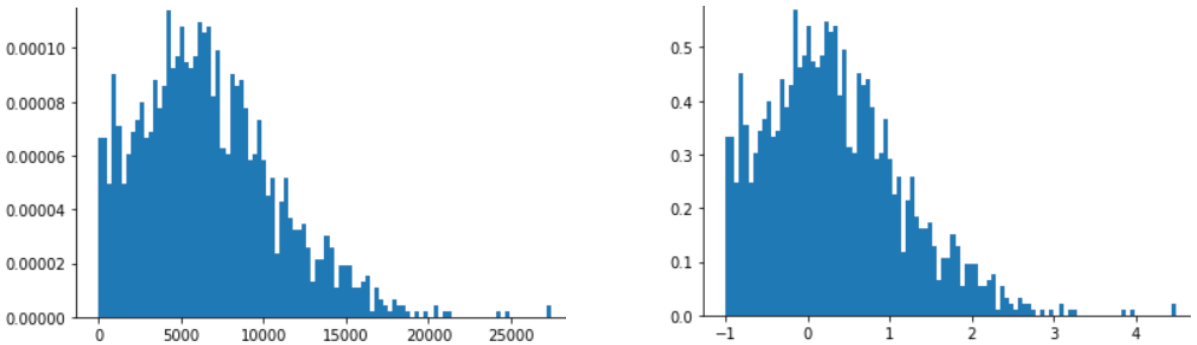
زمانی که داده ها از توزیع نرمال یا توزیعی تا حدودی شبیه توزیع نرمال پیروی می کنند، امتیاز Z انتخاب خوبی است.
توجه داشته باشید که برخی از توزیعها ممکن است در محدوده وسیعی از آنها نرمال باشند، اما همچنان دارای مقادیر پرت شدید هستند. برای مثال، تقریباً تمام نقاط یک ویژگی net_worth ممکن است به طور منظم در 3 انحراف استاندارد قرار بگیرند، اما چند نمونه از این ویژگی میتواند صدها انحراف استاندارد از میانگین فاصله داشته باشد. در این شرایط، میتوانید مقیاس Z-score را با شکل دیگری از نرمالسازی (معمولاً برش) ترکیب کنید تا این وضعیت را مدیریت کنید.
تمرین: درک خود را بررسی کنید
فرض کنید مدل شما روی یک ویژگی به نامheight تمرین می کند که قد بالغ ده میلیون زن را در خود جای می دهد. آیا مقیاس بندی Z-score یک تکنیک نرمال سازی خوب برای height است؟ چرا یا چرا نه؟ مقیاس بندی ورود به سیستم
مقیاس لاگ لگاریتم مقدار خام را محاسبه می کند. در تئوری، لگاریتم می تواند هر پایه ای باشد. در عمل، مقیاس log معمولاً لگاریتم طبیعی (ln) را محاسبه می کند.
مقیاس ثبت زمانی مفید است که داده ها با توزیع قانون توان مطابقت داشته باشند. به طور معمول، توزیع قانون قدرت به صورت زیر است:
- مقادیر پایین
Xدارای مقادیر بسیار بالایYهستند. - با افزایش مقادیر
X، مقادیرYبه سرعت کاهش می یابد. در نتیجه، مقادیر بالایXدارای مقادیر بسیار پایینYهستند.
رتبه بندی فیلم ها نمونه خوبی از توزیع قانون قدرت است. در شکل زیر توجه کنید:
- تعداد کمی از فیلم ها رتبه بندی کاربران زیادی دارند. (مقادیر پایین
Xدارای مقادیر بالایYهستند.) - اکثر فیلم ها رتبه بندی کاربران بسیار کمی دارند. (مقادیر بالای
Xدارای مقادیر پایینYهستند.)
مقیاس لاگ توزیع را تغییر می دهد، که به آموزش مدلی کمک می کند که پیش بینی های بهتری انجام دهد.

به عنوان مثال دوم، فروش کتاب با توزیع قانون قدرت مطابقت دارد زیرا:
- اکثر کتاب های منتشر شده تعداد کمی از نسخه ها، شاید یک یا دویست نسخه به فروش می رسند.
- برخی از کتاب ها تعداد متوسطی از نسخه ها را به هزاران می فروشند.
- تنها تعداد کمی از پرفروشترینها بیش از یک میلیون نسخه فروش خواهند داشت.
فرض کنید در حال آموزش یک مدل خطی هستید تا رابطه مثلاً جلد کتاب با فروش کتاب را پیدا کنید. یک آموزش مدل خطی در مورد ارزشهای خام باید چیزی در مورد جلد کتابهایی پیدا کند که یک میلیون نسخه میفروشند که 10000 جلد قویتر از جلد کتابهایی است که فقط 100 نسخه میفروشند. با این حال، مقیاس بندی ورود به سیستم تمام ارقام فروش، این کار را بسیار امکان پذیرتر می کند. برای مثال، لاگ 100 عبارت است از:
~4.6 = ln(100)
در حالی که لاگ 1,000,000 برابر است با:
~13.8 = ln(1,000,000)
بنابراین، لاگ 1,000,000 فقط حدوداً سه برابر بزرگتر از 100 است. احتمالاً می توانید تصور کنید که جلد کتاب پرفروش تقریباً سه برابر (به نوعی) قدرتمندتر از یک جلد کتاب پرفروش باشد.
بریدن
برش تکنیکی برای به حداقل رساندن تأثیر نقاط پرت شدید است. به طور خلاصه، برش معمولاً مقدار نقاط پرت را به یک مقدار حداکثر مشخص میپوشاند (کاهش میدهد). بریدن ایده عجیبی است، و با این حال، می تواند بسیار موثر باشد.
برای مثال، مجموعه داده ای را تصور کنید که حاوی ویژگی به نام roomsPerPerson است که تعداد اتاق ها (کل اتاق ها تقسیم بر تعداد ساکنان) را برای خانه های مختلف نشان می دهد. نمودار زیر نشان می دهد که بیش از 99٪ از مقادیر ویژگی با توزیع نرمال مطابقت دارد (تقریباً میانگین 1.8 و انحراف استاندارد 0.7). با این حال، این ویژگی حاوی چند ویژگی پرت است که برخی از آنها بسیار شدید است:
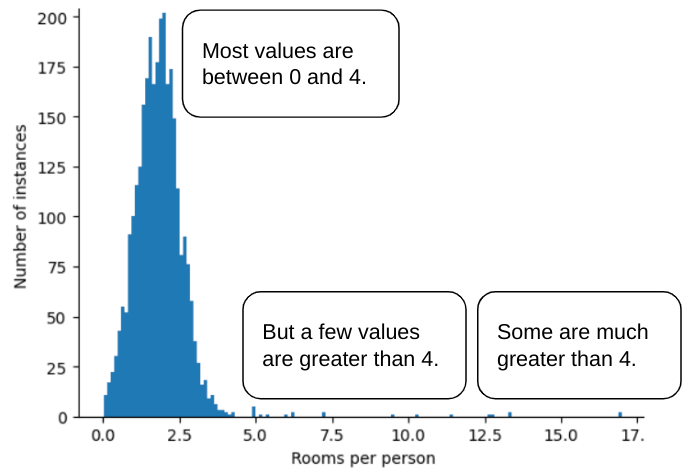
چگونه میتوانید تأثیر آن عوامل پرت را به حداقل برسانید؟ خب، هیستوگرام یک توزیع زوج، یک توزیع نرمال یا یک توزیع قانون توان نیست. اگر به سادگی حداکثر مقدار roomsPerPerson را در یک مقدار دلخواه، مثلاً 4.0، درپوش یا برش دهید ، چه؟
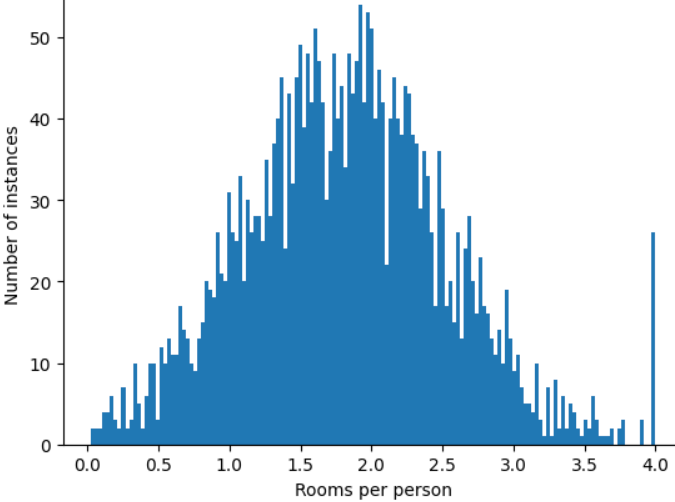
برش دادن مقدار ویژگی در 4.0 به این معنی نیست که مدل شما همه مقادیر بزرگتر از 4.0 را نادیده می گیرد. بلکه به این معنی است که تمام مقادیری که بیشتر از 4.0 بودند اکنون به 4.0 تبدیل می شوند. این تپه عجیب و غریب در 4.0 را توضیح می دهد. با وجود آن تپه، مجموعه ویژگی های مقیاس شده اکنون مفیدتر از داده های اصلی است.
یک ثانیه صبر کن آیا واقعاً می توانید هر مقدار پرت را به آستانه بالایی دلخواه کاهش دهید؟ هنگام آموزش یک مدل، بله.
شما همچنین می توانید مقادیر را پس از اعمال سایر اشکال نرمال سازی، کلیپ کنید. به عنوان مثال، فرض کنید از مقیاس بندی Z-score استفاده می کنید، اما چند عدد پرت مقادیر مطلق بسیار بزرگتر از 3 دارند. در این مورد، می توانید:
- امتیاز Z بزرگتر از 3 را گیره دهید تا دقیقاً 3 شود.
- امتیاز Z را کمتر از -3 بگیرید تا دقیقاً -3 شود.
Clipping مانع از فهرست شدن بیش از حد مدل شما در داده های بی اهمیت می شود. با این حال، برخی از نقاط پرت در واقع مهم هستند، بنابراین مقادیر را با دقت برش دهید.
خلاصه ای از تکنیک های عادی سازی
| تکنیک عادی سازی | فرمول | زمان استفاده |
|---|---|---|
| مقیاس بندی خطی | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | هنگامی که ویژگی عمدتاً به طور یکنواخت در سراسر محدوده توزیع شده است. به شکل تخت |
| مقیاس بندی Z-score | $$ x' = \frac{x - μ}{σ}$$ | هنگامی که ویژگی به طور معمول توزیع شده است (اوج نزدیک به میانگین). زنگی شکل |
| مقیاس بندی ورود به سیستم | $$ x' = log(x)$$ | هنگامی که توزیع ویژگی سنگین است حداقل در هر دو طرف دم. به شکل دم سنگین |
| بریدن | اگر $x > max$، $x' = max$ را تنظیم کنید اگر $x <min$، $x' = min$ را تنظیم کنید | زمانی که ویژگی دارای نقاط پرت شدید باشد. |
تمرین: دانش خود را بیازمایید

فرض کنید در حال توسعه مدلی هستید که بهره وری یک مرکز داده را بر اساس دمای اندازه گیری شده در مرکز داده پیش بینی می کند. تقریباً همه مقادیر temperature در مجموعه داده شما بین 15 تا 30 (سلسیوس) قرار می گیرند، به استثنای موارد زیر:
- یک یا دو بار در سال، در روزهای بسیار گرم، مقدار کمی بین 31 تا 45 در
temperatureثبت می شود. - هر 1000 نقطه
temperatureبه جای دمای واقعی روی 1000 تنظیم می شود.
کدام یک روش نرمال سازی معقول برای temperature خواهد بود؟
مقادیر 1000 اشتباه هستند و به جای بریده شدن باید حذف شوند.
مقادیر بین 31 و 45 نقاط داده قانونی هستند. برش دادن احتمالاً ایده خوبی برای این مقادیر خواهد بود، با فرض اینکه مجموعه داده شامل نمونه های کافی در این محدوده دما نباشد تا مدل را برای پیش بینی های خوب آموزش دهد. با این حال، در حین استنباط، توجه داشته باشید که مدل بریده شده برای دمای 45 همان پیش بینی را برای دمای 35 انجام می دهد.
