ข้อมูลตัวเลข: การทำให้เป็นมาตรฐาน

หลังจากตรวจสอบข้อมูลผ่านเทคนิคทางสถิติและการแสดงภาพแล้ว คุณควรเปลี่ยนรูปแบบข้อมูลในลักษณะที่จะช่วยให้โมเดลได้รับการฝึกอย่างมีประสิทธิภาพมากขึ้น เป้าหมายของการปรับให้เป็นมาตรฐานคือการเปลี่ยนรูปแบบฟีเจอร์ให้อยู่ในระดับที่คล้ายกัน ตัวอย่างเช่น ลองพิจารณาฟีเจอร์ 2 อย่างต่อไปนี้

• ฟีเจอร์ X อยู่ในช่วง 154 ถึง 24,917,482
• ฟีเจอร์ Y อยู่ในช่วง 5 ถึง 22

ฟีเจอร์ทั้ง 2 อย่างนี้มีช่วงที่แตกต่างกันมาก การทำให้มาตรฐานอาจดัดแปลง X และ Y เพื่อให้อยู่ในช่วงใกล้เคียงกัน เช่น 0 ถึง 1

การแปลงค่าให้เป็นมาตรฐานมีประโยชน์ดังนี้

• ช่วยให้โมเดลเข้าใกล้ค่าที่ถูกต้องได้เร็วขึ้นระหว่างการฝึก เมื่อฟีเจอร์ต่างๆ มีช่วงต่างกัน การลดเชิงลาดอาจ "ตีกลับ" และทำให้การทำงานช้าลง อย่างไรก็ตาม เครื่องมือเพิ่มประสิทธิภาพขั้นสูงอย่าง Adagrad และ Adam จะป้องกันปัญหานี้ด้วยการเปลี่ยนอัตราการเรียนรู้ที่มีประสิทธิภาพเมื่อเวลาผ่านไป
• ช่วยให้โมเดลคาดการณ์ได้ดีขึ้น เมื่อฟีเจอร์ต่างๆ มีช่วงต่างกัน โมเดลที่ได้อาจทําการคาดการณ์ที่มีประโยชน์น้อยลง
• ช่วยหลีกเลี่ยง "กับดัก NaN" เมื่อค่าของฟีเจอร์สูงมาก NaN เป็นตัวย่อของnot a number เมื่อค่าในโมเดลเกินขีดจำกัดความแม่นยำของทศนิยม ระบบจะตั้งค่าเป็น NaN แทนตัวเลข เมื่อตัวเลข 1 รายการในโมเดลกลายเป็น NaN ตัวเลขอื่นๆ ในโมเดลก็จะกลายเป็น NaN ด้วย
• ช่วยให้โมเดลเรียนรู้น้ำหนักที่เหมาะสมสําหรับแต่ละฟีเจอร์ หากไม่มีการปรับขนาดฟีเจอร์ โมเดลจะให้ความสำคัญกับฟีเจอร์ที่มีช่วงกว้างมากเกินไปและไม่ให้ความสำคัญกับฟีเจอร์ที่มีช่วงแคบมากพอ

เราขอแนะนําให้ทำให้ฟีเจอร์ที่เป็นตัวเลขเป็นมาตรฐานโดยครอบคลุมช่วงที่แตกต่างกันอย่างชัดเจน (เช่น อายุและรายได้) นอกจากนี้ เราขอแนะนําให้ทำให้ฟีเจอร์ตัวเลขรายการเดียวเป็นมาตรฐานซึ่งครอบคลุมช่วงกว้าง เช่น city population.

คําเตือน: หากปรับมาตรฐานฟีเจอร์ระหว่างการฝึกอบรม คุณต้องปรับมาตรฐานฟีเจอร์นั้นด้วยเมื่อทําการคาดการณ์

ลองพิจารณา 2 ฟีเจอร์ต่อไปนี้

• ค่าต่ำสุดของฟีเจอร์ A คือ -0.5 และค่าสูงสุดคือ +0.5
• ค่าต่ำสุดของฟีเจอร์ B คือ -5.0 และค่าสูงสุดคือ +5.0

ฟีเจอร์ A และฟีเจอร์ B มีช่วงแคบกว่าเมื่อเทียบกับฟีเจอร์อื่นๆ อย่างไรก็ตาม ช่วงของฟีเจอร์ B กว้างกว่าช่วงของฟีเจอร์ A 10 เท่า ดังนั้น

• ในช่วงเริ่มต้นการฝึกโมเดลจะถือว่าฟีเจอร์ B "สำคัญ" กว่าฟีเจอร์ A 10 เท่า
• การฝึกอบรมจะใช้เวลานานกว่าที่ควรจะเป็น
• โมเดลที่ได้อาจไม่เหมาะสม

ความเสียหายโดยรวมเนื่องจากการไม่ทำให้เป็นมาตรฐานจะค่อนข้างน้อย อย่างไรก็ตาม เรายังคงแนะนําให้ทำให้ฟีเจอร์ ก และ ข เป็นมาตรฐานเดียวกัน เช่น -1.0 ถึง +1.0

มาดูฟีเจอร์ 2 รายการที่มีช่วงความหลากหลายมากกว่ากัน

• ค่าต่ำสุดของฟีเจอร์ C คือ -1 และค่าสูงสุดคือ +1
• ค่าต่ำสุดของฟีเจอร์ D คือ +5000 และค่าสูงสุดคือ +1,000,000,000

หากคุณไม่ได้ทำให้ฟีเจอร์ C และฟีเจอร์ D เป็นมาตรฐาน โมเดลของคุณอาจทำงานได้ไม่ดีที่สุด นอกจากนี้ การฝึกอบรมจะใช้เวลานานขึ้นมากในการบรรจบหรืออาจบรรจบไม่สำเร็จเลย

ส่วนนี้จะกล่าวถึงวิธีการทําให้เป็นมาตรฐานที่นิยมกัน 3 วิธี ได้แก่

• การปรับขนาดเชิงเส้น
• การปรับขนาดคะแนนมาตรฐาน (Z-Score)
• การปรับขนาดบันทึก

ส่วนนี้ยังครอบคลุมการตัดด้วย แม้ว่าจะไม่ใช่เทคนิคการปรับให้เป็นมาตรฐานอย่างแท้จริง แต่การตัดทอนจะควบคุมฟีเจอร์ตัวเลขที่ควบคุมยากให้อยู่ในช่วงที่จะสร้างโมเดลที่ดีขึ้นได้

การปรับสเกลเชิงเส้น

การปรับสเกลเชิงเส้น (มักเรียกสั้นๆ ว่าการปรับสเกล) หมายถึงการเปลี่ยนค่าทศนิยมจากช่วงปกติเป็นช่วงมาตรฐาน ซึ่งมักจะเป็น 0 ถึง 1 หรือ -1 ถึง +1

คลิกไอคอนเพื่อดูคณิตศาสตร์

ใช้สูตรต่อไปนี้เพื่อปรับขนาดเป็นช่วงมาตรฐาน 0 ถึง 1 โดยรวม

$$ x' = (x - x_{min}) / (x_{max} - x_{min}) $$

where:

• $x'$ คือค่าที่ปรับขนาด
• $x$ คือค่าเดิม
• $x_{min}$ คือค่าต่ำสุดในชุดข้อมูลของฟีเจอร์นี้
• $x_{max}$ คือค่าสูงสุดในชุดข้อมูลของฟีเจอร์นี้

ตัวอย่างเช่น ลองพิจารณาฟีเจอร์ชื่อ quantity ที่มีช่วงค่าตามปกติ 100 ถึง 900 สมมติว่าค่าตามปกติของ quantity ในตัวอย่างหนึ่งๆ คือ 300 คุณจึงคํานวณค่ามาตรฐานของ 300 ได้โดยทำดังนี้

• $x$ = 300
• $x_{min}$ = 100
• $x_{max}$ = 900

x' = (300 - 100) / (900 - 100)
x' = 200 / 800
x' = 0.25

---

การกําหนดขนาดแบบเชิงเส้นเป็นตัวเลือกที่ดีเมื่อเป็นไปตามเงื่อนไขทั้งหมดต่อไปนี้

• ขอบเขตล่างและขอบเขตบนของข้อมูลไม่เปลี่ยนแปลงมากนักเมื่อเวลาผ่านไป
• ฟีเจอร์มีค่าผิดปกติน้อยหรือไม่มีเลย และค่าผิดปกติเหล่านั้นไม่ได้อยู่ในช่วงสุดขั้ว
• องค์ประกอบมีการกระจายอย่างสม่ำเสมอทั่วทั้งช่วง กล่าวคือ ฮิสโตแกรมจะแสดงแท่งที่มีความสูงใกล้เคียงกันสำหรับค่าส่วนใหญ่

สมมติว่า age เป็นฟีเจอร์ การปรับขนาดเชิงเส้นเป็นเทคนิคการปรับมาตรฐานที่ดีสําหรับ age เนื่องจาก

• ขอบเขตล่างและขอบเขตบนโดยประมาณคือ 0 ถึง 100
• age มีค่าที่ผิดปกติในเปอร์เซ็นต์ค่อนข้างต่ำ มีเพียงประมาณ 0.3% ของประชากรที่มีอายุมากกว่า 100 ปี
• แม้ว่าบางวัยจะมีตัวอย่างที่ดีกว่ากลุ่มอื่นๆ แต่ชุดข้อมูลขนาดใหญ่ควรมีตัวอย่างที่เพียงพอสำหรับทุกวัย

หมายเหตุ: ฟีเจอร์ในชีวิตจริงส่วนใหญ่ไม่เป็นไปตามเกณฑ์ทั้งหมดสำหรับการปรับขนาดเชิงเส้น โดยทั่วไปแล้วการปรับขนาดคะแนน Z เป็นตัวเลือกการปรับมาตรฐานที่ดีกว่าการปรับขนาดเชิงเส้น

แบบฝึกหัด: ทดสอบความเข้าใจ

สมมติว่าโมเดลของคุณมีฟีเจอร์ชื่อ net_worth ที่เก็บมูลค่าสุทธิของบุคคลต่างๆ การปรับขนาดเชิงเส้นเป็นเทคนิคการปรับให้เป็นมาตรฐานที่ดีสำหรับ net_worth ไหม เพราะเหตุใด

คลิกไอคอนเพื่อดูคำตอบ

คําตอบ: การปรับขนาดเชิงเส้นเป็นตัวเลือกที่ไม่เหมาะสําหรับการปรับค่า net_worth ฟีเจอร์นี้มีค่าที่ผิดปกติจำนวนมาก และค่าต่างๆ ไม่ได้กระจายอย่างสม่ำเสมอในช่วงหลัก ผู้คนส่วนใหญ่จะอยู่ในแถบแคบๆ ของช่วงโดยรวม

---

การปรับขนาดคะแนนมาตรฐาน (Z-Score)

คะแนน Z คือจํานวนค่าเบี่ยงเบนมาตรฐานของค่าหนึ่งๆ จากค่าเฉลี่ย เช่น ค่าที่ค่าเบี่ยงเบนมาตรฐานมากกว่าค่าเฉลี่ย 2 เท่าจะมีคะแนน z ที่ +2.0 ค่าที่น้อยกว่าค่ามัธยฐาน 1.5 ค่าเบี่ยงเบนมาตรฐานจะมีคะแนน z ที่ -1.5

การนําเสนอองค์ประกอบด้วยการปรับขนาด Z-Score หมายถึงการจัดเก็บ Z-Score ขององค์ประกอบนั้นในเวกเตอร์องค์ประกอบ เช่น รูปภาพต่อไปนี้แสดงฮิสโตแกรม 2 รายการ

• ทางด้านซ้ายคือการกระจายปกติแบบคลาสสิก
• ทางด้านขวาคือการแจกแจงเดียวกันที่ปรับมาตรฐานโดยการปรับขนาดคะแนน z

รูปที่ 4 ข้อมูลดิบ (ซ้าย) เทียบกับคะแนน Z (ขวา) สำหรับการแจกแจงปกติ

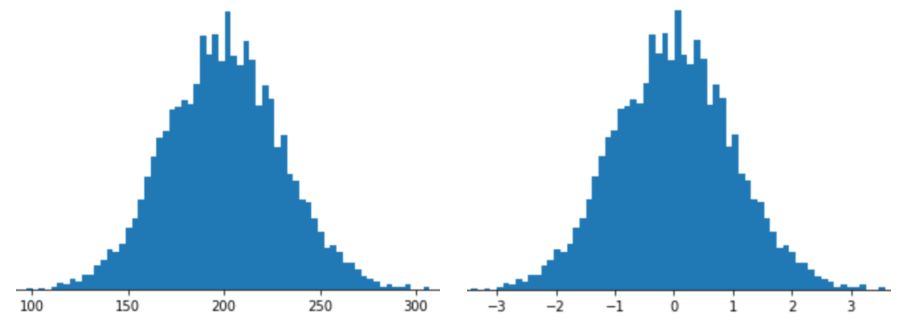
การปรับขนาดคะแนน z ยังเป็นตัวเลือกที่ดีสําหรับข้อมูลอย่างเช่นที่แสดงในรูปภาพต่อไปนี้ ซึ่งมีเพียงการแจกแจงแบบปกติเพียงเล็กน้อย

รูปที่ 5 ข้อมูลดิบ (ซ้าย) เทียบกับการปรับขนาดคะแนน Z (ขวา) สำหรับการแจกแจงแบบปกติที่ไม่ใช่แบบคลาสสิก

คลิกไอคอนเพื่อดูคณิตศาสตร์

ใช้สูตรต่อไปนี้เพื่อทำให้ค่า $x$ เป็นค่ามาตรฐานเพื่อหาคะแนน Z

$$ x' = (x - μ) / σ $$

where:

• $x'$ คือคะแนนมาตรฐาน (Z-Score)
• $x$ คือค่าดิบ กล่าวคือ $x$ คือค่าที่คุณกําลังทำให้เป็นมาตรฐาน
• $μ$ คือค่าเฉลี่ย
• $σ$ คือค่าเบี่ยงเบนมาตรฐาน

เช่น สมมติว่า

• ค่าเฉลี่ย = 100
• ค่าเบี่ยงเบนมาตรฐาน = 20
• original value = 130

ดังนั้น

  Z-score = (130 - 100) / 20
  Z-score = 30 / 20
  Z-score = +1.5

---

คลิกไอคอนเพื่อดูข้อมูลเพิ่มเติมเกี่ยวกับความถี่แบบปกติ

ในการแจกแจงปกติแบบคลาสสิก

• ข้อมูลอย่างน้อย 68.27% มีคะแนน Z อยู่ระหว่าง -1.0 ถึง +1.0
• ข้อมูลอย่างน้อย 95.45% มีคะแนน Z อยู่ระหว่าง -2.0 ถึง +2.0
• ข้อมูลอย่างน้อย 99.73% มีคะแนน Z ระหว่าง -3.0 ถึง +3.0
• ข้อมูลอย่างน้อย 99.994% มีคะแนน Z ระหว่าง -4.0 ถึง +4.0

ดังนั้น จุดข้อมูลที่มีคะแนน z น้อยกว่า -4.0 หรือมากกว่า +4.0 จะพบได้น้อย แต่จุดข้อมูลเหล่านี้เป็นค่าผิดปกติจริงหรือไม่ เนื่องจากค่าที่ผิดปกติเป็นแนวคิดที่ไม่มีคำจำกัดความที่ชัดเจน จึงไม่มีใครบอกได้แน่ชัด โปรดทราบว่าชุดข้อมูลที่มีตัวอย่างจำนวนมากพอจะมีตัวอย่าง "ที่พบไม่บ่อย" เหล่านี้อย่างน้อย 2-3 รายการ ตัวอย่างเช่น ฟีเจอร์ที่มีตัวอย่าง 1, 000 ล้านรายการซึ่งเป็นไปตามการแจกแจงแบบปกติคลาสสิกอาจมีตัวอย่างมากถึง 60,000 รายการที่มีคะแนนอยู่นอกช่วง -4.0 ถึง +4.0

---

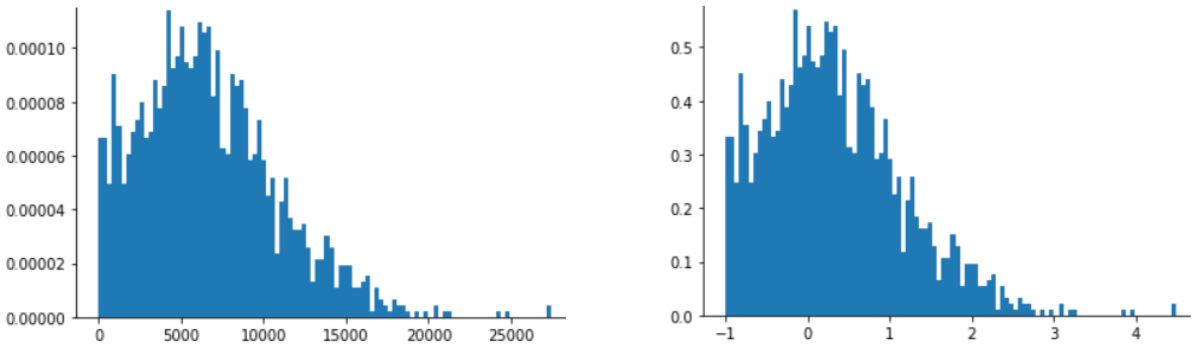
ค่า z เป็นตัวเลือกที่ดีเมื่อข้อมูลเป็นไปตามการแจกแจงแบบปกติหรือการแจกแจงที่คล้ายกับการแจกแจงแบบปกติ

โปรดทราบว่าการแจกแจงบางรายการอาจเป็นไปตามปกติในช่วงส่วนใหญ่ แต่ยังคงมีค่าที่ผิดปกติอย่างมาก ตัวอย่างเช่น จุดเกือบทั้งหมดในฟีเจอร์ net_worth อาจอยู่ในการเบี่ยงเบนมาตรฐาน 3 รายการได้พอดี แต่ตัวอย่างฟีเจอร์นี้ 2-3 รายการอาจอยู่ห่างจากค่าเฉลี่ยหลายร้อยค่าเบี่ยงเบนมาตรฐาน ในสถานการณ์เหล่านี้ คุณสามารถรวมการปรับขนาดคะแนน Z เข้ากับการปรับให้เป็นมาตรฐานรูปแบบอื่น (โดยปกติคือการตัด) เพื่อจัดการกับสถานการณ์นี้

แบบฝึกหัด: ทดสอบความเข้าใจ

สมมติว่าโมเดลของคุณฝึกกับฟีเจอร์ชื่อ height ที่มีข้อมูลความสูงของผู้หญิงวัยผู้ใหญ่ 10 ล้านคน การปรับสเกล Z-Score เป็นเทคนิคการปรับให้เป็นมาตรฐานที่ดีสำหรับ height ไหม เพราะเหตุใด

คลิกไอคอนเพื่อดูคำตอบ

คําตอบ: การปรับขนาดคะแนน z เป็นเทคนิคการปรับมาตรฐานที่ดีสําหรับ height เนื่องจากฟีเจอร์นี้เป็นไปตามการแจกแจงแบบปกติ ตัวอย่าง 10 ล้านรายการแสดงถึงค่าเบี่ยงเบนมาก ซึ่งอาจเป็นค่าเบี่ยงเบนมากพอที่โมเดลจะเรียนรู้รูปแบบเกี่ยวกับคะแนน Z ที่สูงมากหรือต่ำมาก

---

การปรับขนาดบันทึก

การแปลงข้อมูลเป็นลําดับเลขฐาน 10 จะคํานวณลอการิทึมของค่าดิบ ในทางทฤษฎีแล้ว ลอการิทึมอาจเป็นฐานใดก็ได้ แต่ในทางปฏิบัติ การแปลงข้อมูลแบบลอการิทึมมักจะคํานวณลอการิทึมธรรมชาติ (ln)

คลิกไอคอนเพื่อดูคณิตศาสตร์

ใช้สูตรต่อไปนี้เพื่อทำให้ค่า $x$ เป็นมาตรฐานเพื่อเข้าสู่บันทึก

$$ x' = ln(x) $$

where:

• $x'$ คือลอการิทึมธรรมชาติของ $x$
• original value = 54.598

ดังนั้น บันทึกของค่าเดิมจึงมีค่าประมาณ 4.0

  4.0 = ln(54.598)

---

การกําหนดขนาดข้อมูลแบบลอจิกมีประโยชน์เมื่อข้อมูลเป็นไปตามการแจกแจงแบบกฎกำลัง พูดง่ายๆ ก็คือ การแจกแจงของกฎกำลังสองมีลักษณะดังนี้

• ค่าต่ำของ X มีค่า Y สูงมาก
• เมื่อค่าของ X เพิ่มขึ้น ค่าของ Y จะลดลงอย่างรวดเร็ว ดังนั้น X ที่มีค่าสูงจึงมี Y ที่มีค่าต่ำมาก

การจัดประเภทภาพยนตร์เป็นตัวอย่างที่ดีของการแจกแจงแบบกำลังของจำนวน ในรูปภาพต่อไปนี้ ให้สังเกตสิ่งต่อไปนี้

• ภาพยนตร์บางเรื่องมีคะแนนจากผู้ใช้จำนวนมาก (ค่าต่ำของ X มีค่า Y สูง)
• ภาพยนตร์ส่วนใหญ่มีคะแนนจากผู้ใช้น้อยมาก (ค่า X ที่สูงมีค่า Y ที่ต่ำ)

การปรับขนาดข้อมูลบันทึกจะเปลี่ยนการแจกแจง ซึ่งช่วยฝึกโมเดลที่จะทําการคาดการณ์ได้ดีขึ้น

รูปที่ 6 การเปรียบเทียบการแจกแจงข้อมูลดิบกับบันทึก

ตัวอย่างที่ 2 คือ ยอดขายหนังสือเป็นไปตามการแจกแจงแบบกำลังเนื่องจาก

• หนังสือส่วนใหญ่ที่ตีพิมพ์มียอดขายเพียงไม่กี่เล่ม อาจจะ 1-2 ร้อยเล่ม
• หนังสือบางเล่มขายได้จำนวนปานกลางประมาณหลายพันเล่ม
• มีเพียงหนังสือขายดีไม่กี่เล่มเท่านั้นที่จะขายได้มากกว่า 1 ล้านเล่ม

สมมติว่าคุณกําลังฝึกโมเดลเชิงเส้นเพื่อหาความสัมพันธ์ของสิ่งต่างๆ เช่น ปกหนังสือกับยอดขายหนังสือ การฝึกโมเดลเชิงเส้นด้วยค่าดิบจะต้องค้นหาข้อมูลเกี่ยวกับปกหนังสือที่ขายได้ 1 ล้านเล่มซึ่งมีประสิทธิภาพมากกว่าปกหนังสือที่ขายได้เพียง 100 เล่ม 10,000 เท่า อย่างไรก็ตาม การบันทึกการปรับขนาดตัวเลขยอดขายทั้งหมดทําให้งานนี้เป็นไปได้จริงมากขึ้น เช่น ลอการิทึมของ 100 คือ

  ~4.6 = ln(100)

ขณะที่บันทึกของ 1,000,000 คือ

  ~13.8 = ln(1,000,000)

ดังนั้น ลอgarithm ของ 1,000,000 จึงมีค่ามากกว่าลอgarithm ของ 100 เพียงประมาณ 3 เท่า คุณอาจจินตนาการได้ว่าภาพปกหนังสือขายดีมีประสิทธิภาพมากกว่า (ในบางแง่) กว่าภาพปกหนังสือที่ขายได้น้อยประมาณ 3 เท่า

การตัด

การตัดเป็นเทคนิคในการลดอิทธิพลของค่าที่ผิดปกติมาก กล่าวโดยย่อคือ การตัดมักจะจำกัด (ลด) ค่าของค่าเบี่ยงเบนมาตรฐานให้เป็นค่าสูงสุดที่เฉพาะเจาะจง การคลิปเป็นแนวคิดที่แปลก แต่กลับมีประสิทธิภาพมาก

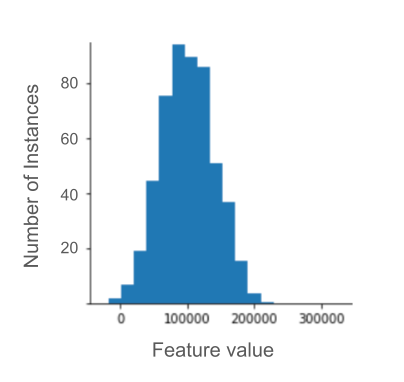
ตัวอย่างเช่น ลองจินตนาการถึงชุดข้อมูลที่มีองค์ประกอบชื่อ roomsPerPerson ซึ่งแสดงจํานวนห้อง (จํานวนห้องทั้งหมดหารด้วยจํานวนผู้พักอาศัย) สําหรับบ้านหลังต่างๆ ผังต่อไปนี้แสดงให้เห็นว่าค่าฟีเจอร์มากกว่า 99% เป็นไปตามการแจกแจงปกติ (ค่าเฉลี่ยโดยประมาณคือ 1.8 และค่าเบี่ยงเบนมาตรฐานคือ 0.7) อย่างไรก็ตาม ฟีเจอร์นี้มีข้อผิดพลาดบางประการ ซึ่งบางรายการก็รุนแรง

รูปที่ 7 ส่วนใหญ่เป็นปกติ แต่ก็ไม่ปกติทั้งหมด

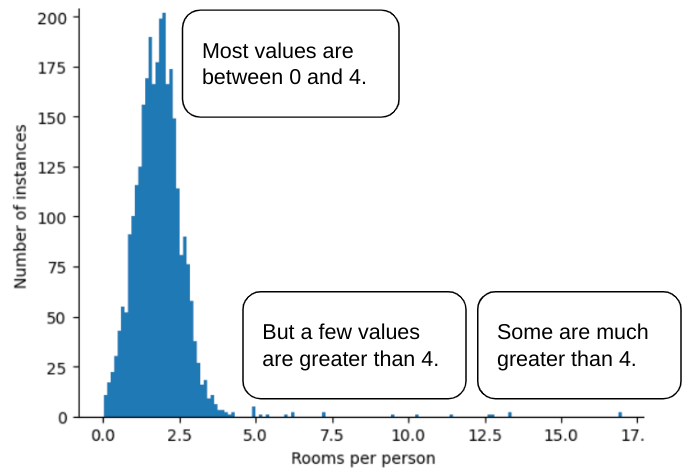
คุณลดอิทธิพลของค่าผิดปกติสุดขั้วเหล่านั้นได้อย่างไร ฮิสโตแกรมไม่ใช่การแจกแจงแบบสม่ำเสมอ การแจกแจงแบบปกติ หรือการแจกแจงแบบกฎกำลัง จะเกิดอะไรขึ้นหากคุณจำกัดหรือตัดค่าสูงสุดของ roomsPerPerson ที่ค่าที่กำหนดเอง เช่น 4.0

รูปที่ 8 การตัดค่าองค์ประกอบที่ 4.0

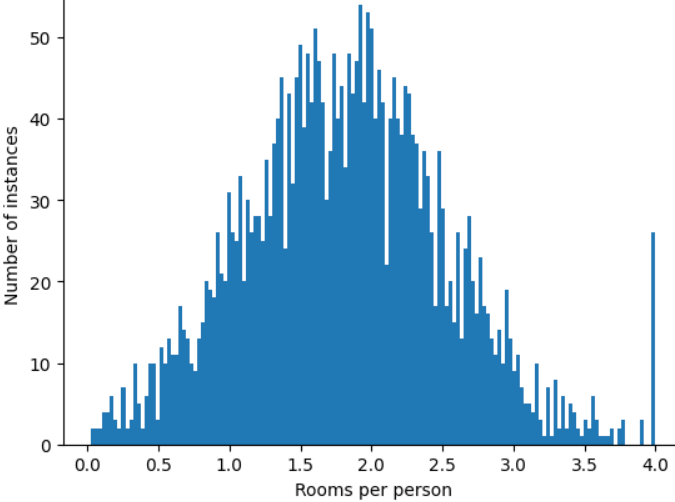
การจำกัดค่าฟีเจอร์ที่ 4.0 ไม่ได้หมายความว่าโมเดลจะละเว้นค่าที่มากกว่า 4.0 ทั้งหมด แต่หมายความว่าค่าทั้งหมดที่มากกว่า 4.0 จะกลายเป็น 4.0 ซึ่งอธิบายถึงเนินแปลกๆ ที่ 4.0 อย่างไรก็ตาม ตอนนี้ชุดฟีเจอร์ที่ปรับขนาดแล้วมีประโยชน์มากกว่าข้อมูลเดิม

เดี๋ยวก่อน คุณลดค่าที่ผิดปกติทุกค่าให้อยู่ต่ำกว่าเกณฑ์บนที่กำหนดเองได้ไหม ใช่ เมื่อฝึกโมเดล

นอกจากนี้ คุณยังตัดค่าหลังจากใช้การทำให้เป็นมาตรฐานรูปแบบอื่นๆ ได้ด้วย เช่น สมมติว่าคุณใช้การปรับขนาดคะแนน Z แต่ค่าที่ผิดปกติบางค่ามีค่าสัมบูรณ์มากกว่า 3 มาก ในกรณีนี้ คุณจะทำสิ่งต่อไปนี้ได้

• ตัดคะแนน Z ที่มากกว่า 3 ให้เหลือ 3
• ตัด Z-score ที่น้อยกว่า -3 ให้เท่ากับ -3

การตัดข้อมูลจะช่วยป้องกันไม่ให้โมเดลจัดทําดัชนีข้อมูลที่ไม่สําคัญมากเกินไป อย่างไรก็ตาม ค่าที่ผิดปกติบางค่าก็มีความสำคัญ ดังนั้นให้ตัดค่าอย่างระมัดระวัง

สรุปเทคนิคการปรับมาตรฐาน

เทคนิคการปรับมาตรฐานที่ดีที่สุดคือเทคนิคที่ได้ผลจริง ดังนั้นลองใช้แนวคิดใหม่ๆ หากคิดว่าจะเหมาะกับการแจกแจงฟีเจอร์ของคุณ

เทคนิคการปรับให้เป็นมาตรฐาน	สูตร	กรณีที่ควรใช้
การปรับสเกลเชิงเส้น	$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$	เมื่อองค์ประกอบมีการกระจายอย่างสม่ำเสมอในหลากหลายที่
การปรับขนาดคะแนนมาตรฐาน (Z-Score)	$$ x' = \frac{x - μ}{σ}$$	เมื่อการแจกแจงฟีเจอร์ไม่มีค่าที่ผิดปกติมาก
การปรับขนาดบันทึก	$$ x' = log(x)$$	เมื่อฟีเจอร์เป็นไปตามกฎกำลัง
การตัด	หาก $x > max$ ให้ตั้งค่า $x' = max$ หาก $x < min$ ให้ตั้งค่า $x' = min$	เมื่อฟีเจอร์มีค่าที่ผิดปกติมาก

แบบฝึกหัด: ทดสอบความรู้

เทคนิคใดเหมาะสําหรับการปรับมาตรฐานฟีเจอร์ที่มีการแจกแจงต่อไปนี้มากที่สุด

การปรับขนาดคะแนนมาตรฐาน (Z-Score)

โดยทั่วไปจุดข้อมูลจะเป็นไปตามการแจกแจงแบบปกติ ดังนั้นการปรับขนาดคะแนน z จะบังคับให้จุดข้อมูลอยู่ในช่วง –3 ถึง +3

การปรับสเกลเชิงเส้น

โปรดอ่านการพูดคุยเกี่ยวกับเทคนิคการปรับมาตรฐานในหน้านี้ แล้วลองอีกครั้ง

การปรับขนาดบันทึก

โปรดอ่านการพูดคุยเกี่ยวกับเทคนิคการปรับมาตรฐานในหน้านี้ แล้วลองอีกครั้ง

การตัด

โปรดอ่านการพูดคุยเกี่ยวกับเทคนิคการปรับมาตรฐานในหน้านี้ แล้วลองอีกครั้ง

สมมติว่าคุณกําลังพัฒนาโมเดลที่คาดการณ์ประสิทธิภาพของศูนย์ข้อมูลตามอุณหภูมิที่วัดได้ภายในศูนย์ข้อมูล ค่า temperature เกือบทั้งหมดในชุดข้อมูลอยู่ในช่วง 15-30 (องศาเซลเซียส) โดยมีข้อยกเว้นต่อไปนี้

• 1 หรือ 2 ครั้งต่อปีในวันที่อากาศร้อนจัด ระบบบันทึกค่า 2-3 ค่าระหว่าง 31 ถึง 45 ใน temperature
• ระบบจะตั้งค่าจุดที่ 1,000 ในทุกๆ temperature เป็น 1,000 แทนอุณหภูมิจริง

เทคนิคการปรับมาตรฐานที่สมเหตุสมผลสําหรับ temperature คืออะไร

ตัดค่าที่ผิดปกติระหว่าง 31 ถึง 45 แต่ลบค่าที่ผิดปกติซึ่งมีค่า 1,000

ค่า 1,000 เป็นค่าที่ผิดพลาดและควรลบออกแทนที่จะตัด

ค่าระหว่าง 31 ถึง 45 เป็นจุดข้อมูลที่ถูกต้อง การจำกัดค่าเหล่านี้อาจเป็นความคิดที่ดี ในกรณีที่ชุดข้อมูลไม่มีตัวอย่างมากพอในช่วงอุณหภูมินี้เพื่อฝึกโมเดลให้คาดการณ์ได้ดี อย่างไรก็ตาม ในระหว่างการอนุมาน โปรดทราบว่าโมเดลที่ตัดข้อมูลออกจะคาดการณ์อุณหภูมิ 45 องศาเซลเซียสเหมือนกับอุณหภูมิ 35 องศาเซลเซียส

ตัดค่าที่ผิดปกติทั้งหมด

โปรดอ่านการพูดคุยเกี่ยวกับเทคนิคการปรับมาตรฐานในหน้านี้ แล้วลองอีกครั้ง

ลบค่าที่ผิดปกติทั้งหมด

โปรดอ่านการพูดคุยเกี่ยวกับเทคนิคการปรับมาตรฐานในหน้านี้ แล้วลองอีกครั้ง

ลบค่าที่ผิดปกติระหว่าง 31 ถึง 45 แต่ตัดค่าที่ผิดปกติซึ่งมีค่า 1,000

โปรดอ่านการพูดคุยเกี่ยวกับเทคนิคการปรับมาตรฐานในหน้านี้ แล้วลองอีกครั้ง

คําสําคัญ:

• การตัด
• กับดัก NaN
• การปรับมาตรฐาน
• การปรับขนาด
• การปรับให้เป็นมาตรฐานตามคะแนน z