通过统计和可视化技术检查数据后,您应以有助于模型更有效地训练的方式转换数据。归一化的目标是将特征转换为相似的比例。例如,请考虑以下两项功能:
- 特征
X的范围为 154 到 24,917,482。 - 特征
Y的范围为 5 到 22。
这两个特征的范围差异很大。归一化可能会处理 X 和 Y,使它们跨越相似的范围(可能为 0 到 1)。
归一化具有以下优势:
- 有助于模型在训练期间更快地收敛。当不同特征的范围不同时,梯度下降可能会“反弹”,从而减慢收敛速度。不过,Adagrad 和 Adam 等更高级的优化器会随时间改变有效学习速率,从而避免此问题。
- 有助于模型做出更准确的推理预测。 如果不同特征的范围不同,生成的模型可能会做出不太有用的预测。
- 有助于在特征值非常高时避免“NaN 陷阱”。
NaN 是非数字的缩写。当模型中的某个值超出浮点精确率限制时,系统会将该值设置为
NaN而不是某个数字。当模型中的一个数值变成 NaN 时,模型中的其他数值最终也会变成 NaN。 - 帮助模型为每个特征确定合适的权重。如果不进行特征缩放,模型会过于关注范围较大的特征,而对范围较小的特征关注不足。
我们建议对涵盖明显不同范围的数值特征(例如年龄和收入)进行归一化处理。我们还建议对涵盖广泛范围的单个数值特征(例如 city population.)进行归一化处理
请考虑以下两项功能:
- 特征
A的最低值为 -0.5,最高值为 +0.5。 - 特征
B的最低值为 -5.0,最高值为 +5.0。
特征 A 和特征 B 的跨度相对较窄。不过,功能 B 的跨度是功能 A 的 10 倍。因此:
- 在训练开始时,模型会假设特征
B比特征A“重要”十倍。 - 训练时间会比预期长。
- 生成的模型可能不是最佳模型。
不进行归一化处理造成的总体损害相对较小;不过,我们仍然建议将特征 A 和特征 B 归一化到相同的范围,例如 -1.0 到 +1.0。
现在,我们来考虑两个范围差异更大的特征:
- 特征
C的最低值为 -1,最高值为 +1。 - 功能
D的最低值为 +5000,最高值为 +1,000,000,000。
如果不对特征 C 和特征 D 进行归一化处理,模型很可能无法达到最佳效果。此外,训练将需要更长时间才能收敛,甚至可能完全无法收敛!
本部分介绍了三种常用的归一化方法:
- 线性缩放
- Z 分数缩放
- 对数缩放
本部分还将介绍剪辑。虽然剪裁不是真正的归一化技术,但它确实可以将不规则的数值特征限制在可生成更好模型的范围内。
线性缩放
线性缩放(通常简称为缩放)是指将浮点值从其自然范围转换为标准范围(通常为 0 到 1 或 -1 到 +1)。
如果满足以下所有条件,线性缩放是不错的选择:
- 数据的下限和上限不会随时间发生太大变化。
- 特征包含的离群值很少或没有,并且这些离群值并不极端。
- 该特征在其范围内大致呈均匀分布。 也就是说,直方图会显示大致均匀的条形,对应于大多数值。
假设人类 age 是一项功能。线性缩放是 age 的一种很好的归一化技术,原因如下:
- 近似下限和上限为 0 到 100。
age包含的离群值百分比较低。只有约 0.3% 的人口超过 100 岁。- 虽然某些年龄段的代表性可能略好于其他年龄段,但大型数据集应包含所有年龄段的充足示例。
练习:检查您的理解情况
假设您的模型有一个名为net_worth 的特征,用于保存不同人员的净资产。线性缩放是否适合作为 net_worth 的一种归一化技术?请说明原因。
Z 分数缩放
Z 得分是指某个值与平均值相差的标准差数。 例如,比平均值高 2 个标准差的值的 Z 得分为 +2.0。比平均值低 1.5 个标准差的值的 Z 得分为 -1.5。
使用 Z 得分缩放表示特征意味着将该特征的 Z 得分存储在特征向量中。例如,下图显示了两个直方图:
- 左侧为经典正态分布。
- 右侧是经过 Z-score 缩放归一化的同一分布。
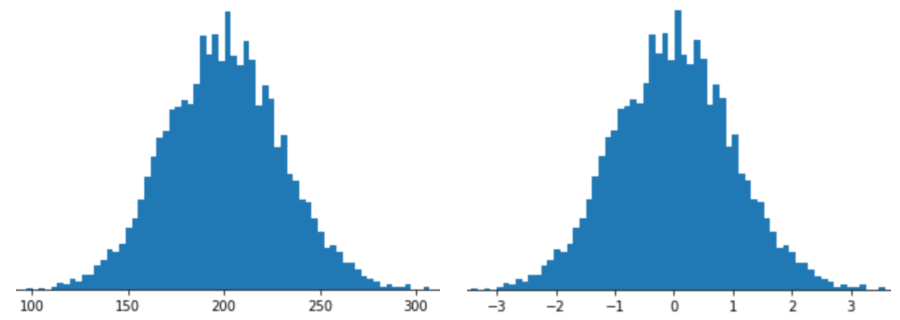
对于下图所示的仅具有模糊正态分布的数据,Z 得分缩放也是一个不错的选择。
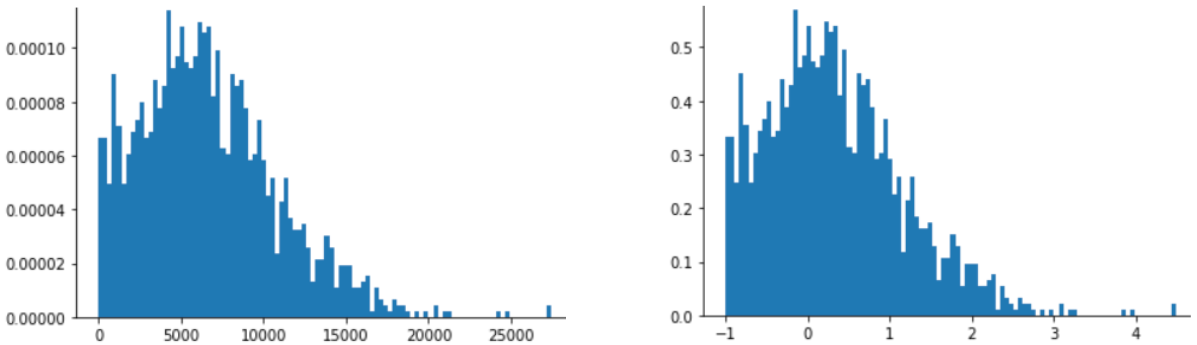
如果数据遵循正态分布或某种程度上类似于正态分布,则 Z 得分是一个不错的选择。
请注意,某些分布可能在其大部分范围内都是正态分布,但仍包含极值离群点。例如,net_worth 特征中的几乎所有点都可能恰好位于 3 个标准差范围内,但此特征的少数几个示例可能与平均值相差数百个标准差。在这种情况下,您可以将 Z 得分缩放与其他形式的归一化(通常是剪裁)相结合来处理这种情况。
练习:检查您的理解情况
假设您的模型基于名为height 的特征进行训练,该特征包含 1,000 万名女性的成人身高。Z-score 缩放是否适合作为 height 的归一化技术?请说明原因。
对数缩放
对数缩放会计算原始值的对数。从理论上讲,对数可以是任意底数;但在实践中,对数缩放通常会计算自然对数 (ln)。
当数据符合幂律分布时,对数缩放很有用。通俗地说,幂律分布如下所示:
X的值较低时,Y的值非常高。- 随着
X值的增加,Y值会快速减小。 因此,X的值较高时,Y的值会非常低。
电影评分是幂律分布的一个很好的例子。在下图中,请注意:
- 有些电影有很多用户评分。(
X的值较低时,Y的值较高。) - 大多数电影的用户评分都很少。(
X的值较高时,Y的值较低。)
对数缩放会改变分布,有助于训练出能够做出更好预测的模型。

再举一个例子,图书销售额符合幂律分布,因为:
- 大多数已出版的图书的销量都非常低,可能只有一两百本。
- 有些书的销量适中,达到数千册。
- 只有少数畅销书的销量会超过 100 万册。
假设您正在训练一个线性模型,以找出图书封面与图书销量之间的关系。如果线性模型基于原始值进行训练,则必须找到畅销百万册的图书封面与仅售出 100 册的图书封面之间相差 10,000 倍的某种特征。 不过,对所有销售数据进行对数缩放可使任务的可行性大大提高。 例如,100 的对数是:
~4.6 = ln(100)
而 1,000,000 的对数是:
~13.8 = ln(1,000,000)
因此,1,000,000 的对数仅比 100 的对数大三倍左右。 您可能可以想象,畅销书的封面在某些方面比销量很低的图书封面强大三倍左右。
裁剪
裁剪是一种可最大限度减少极端离群值影响的技术。简而言之,剪裁通常会将离群值限制(减少)为特定的最大值。剪辑是一个奇怪的想法,但它可能非常有效。
例如,假设有一个数据集包含一个名为 roomsPerPerson 的特征,该特征表示各种房屋的房间数(总房间数除以居住人数)。下图显示,超过 99% 的特征值符合正态分布(大致来说,平均值为 1.8,标准差为 0.7)。不过,该特征包含一些离群值,其中一些是极值:
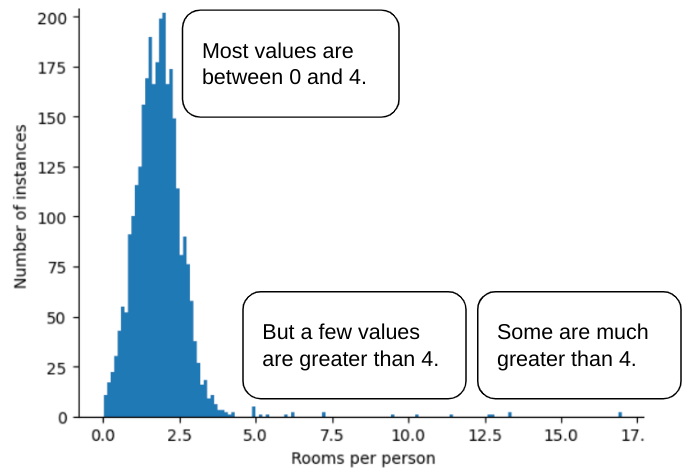
如何最大限度地减少这些极端离群值的影响?直方图不是均匀分布、正态分布或幂律分布。如果我们只是简单地将 roomsPerPerson 的最大值“限制”或“削减”为某个任意值(比如 4.0),会发生什么情况呢?
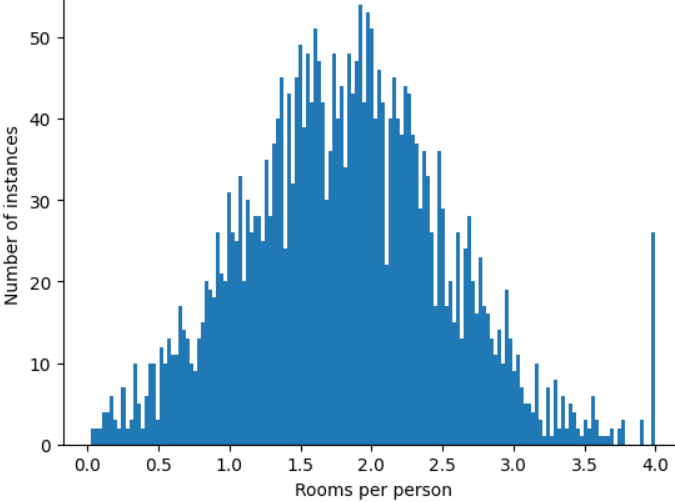
将特征值剪裁为 4.0 并不意味着模型会忽略所有大于 4.0 的值。而是指所有大于 4.0 的值现在都变为 4.0。这解释了 4.0 处的特殊山丘。尽管存在这个山峰,但缩放后的特征集现在比原始数据更有用。
等一下!您真的可以将每个离群值都减少到某个任意上限吗?在训练模型时,是的。
您还可以在应用其他形式的归一化后剪裁值。例如,假设您使用 Z 得分缩放,但少数离群点的绝对值远大于 3。在这种情况下,您可以:
- 将大于 3 的 Z 分数裁剪到正好 3。
- 将 Z 得分小于 -3 的值裁剪为正好 -3。
剪裁可防止模型过度关注不重要的数据。不过,有些离群值实际上很重要,因此请谨慎剪裁值。
归一化技术摘要
| 归一化技术 | 公式 | 适用情形 |
|---|---|---|
| 线性缩放 | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | 当特征在整个范围内大致均匀分布时。 扁平状 |
| Z 分数缩放 | $$ x' = \frac{x - μ}{σ}$$ | 当特征呈正态分布时(峰值接近平均值)。 钟形 |
| 对数缩放 | $$ x' = log(x)$$ | 当特征分布在至少一侧的尾部严重偏斜时。 重尾形 |
| 裁剪 | 如果 $x > max$,则设置 $x' = max$ 如果 $x < min$,则设置 $x' = min$ |
当特征包含极端离群值时。 |
练习:知识测验
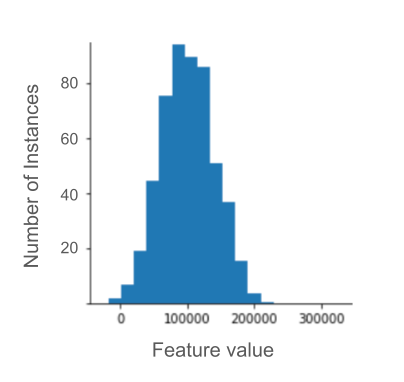
假设您正在开发一个模型,该模型可根据数据中心内部测得的温度预测数据中心的生产力。
数据集中的几乎所有 temperature 值都介于 15 到 30(摄氏度)之间,但以下情况除外:
- 在一年中,极热的天气会出现一到两次,此时
temperature中会记录一些介于 31 到 45 之间的值。 temperature中每第 1,000 个点都设置为 1,000,而不是实际温度。
哪种归一化技术适合用于 temperature?
1,000 的值是错误的,应删除而不是剪裁。
31 到 45 之间的值是合法的数据点。 假设数据集在此温度范围内没有足够的示例来训练模型以做出良好的预测,那么对这些值进行剪裁可能是一个好主意。不过,在推理期间,请注意,剪裁后的模型对 45 度和 35 度的温度做出的预测是相同的。