Parfois, lorsque l'expert en ML dispose de connaissances du domaine suggérant qu'une variable est liée au carré, au cube ou à une autre puissance d'une autre variable, il est utile de créer une fonctionnalité synthétique à partir de l'une des fonctionnalités numériques existantes.
Considérons la répartition des points de données suivante, où les cercles roses représentent une classe ou une catégorie (par exemple, une espèce d'arbre) et les triangles verts une autre classe (ou espèce d'arbre):
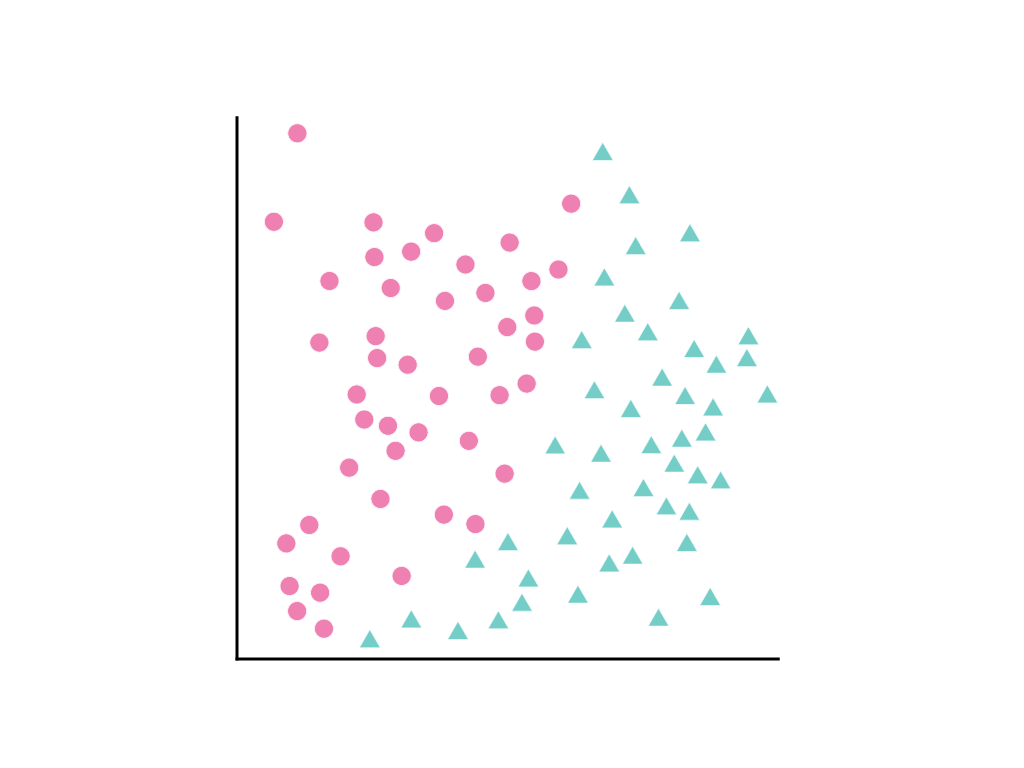
Il est impossible de tracer une ligne droite qui sépare clairement les deux classes, mais il est possible de tracer une courbe qui le fait:
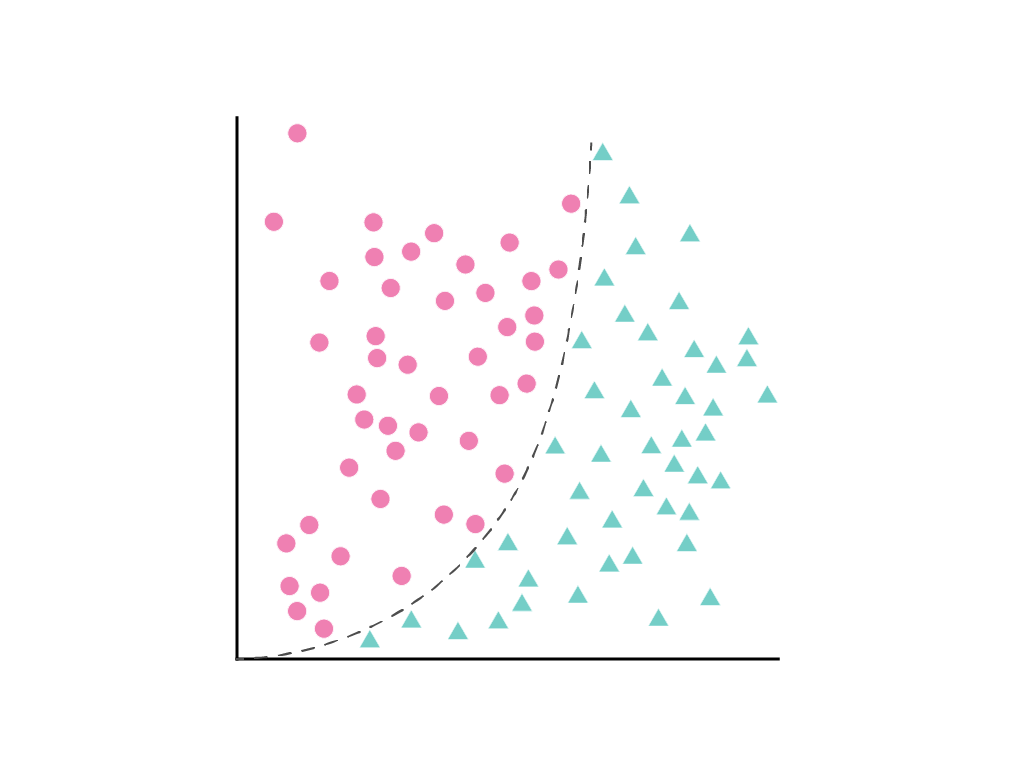
Comme indiqué dans le module de régression linéaire, un modèle linéaire avec une seule caractéristique, $x_1$, est décrit par l'équation linéaire:
Les fonctionnalités supplémentaires sont gérées par l'ajout de termes \(w_2x_2\),\(w_3x_3\), etc.
La descente de gradient trouve la pondération $w_1$ (ou les pondérations\(w_1\), \(w_2\), \(w_3\), dans le cas de fonctionnalités supplémentaires) qui minimise la perte du modèle. Toutefois, les points de données affichés ne peuvent pas être séparés par une ligne. Que puis-je faire ?
Il est possible de conserver l'équation linéaire et d'autoriser la non-linéarité en définissant un nouveau terme, \(x_2\), qui est simplement le carré de \(x_1\) :
Cette caractéristique synthétique, appelée transformation polynomiale, est traitée comme n'importe quelle autre caractéristique. La formule linéaire précédente devient:
Ce problème peut toujours être traité comme un problème de régression linéaire, et les poids déterminés par descente du gradient, comme d'habitude, malgré la présence d'un terme au carré masqué, la transformation polynomiale. Sans modifier la façon dont le modèle linéaire est entraîné, l'ajout d'une transformation polynomiale permet au modèle de séparer les points de données à l'aide d'une courbe de la forme $y = b + w_1x + w_2x^2$.
En règle générale, la caractéristique numérique d'intérêt est multipliée par elle-même, c'est-à-dire élevée à une puissance. Parfois, un professionnel du ML peut faire une estimation éclairée de l'exposant approprié. Par exemple, de nombreuses relations dans le monde physique sont liées à des termes au carré, y compris l'accélération due à la gravité, l'atténuation de la lumière ou du son avec la distance et l'énergie potentielle élastique.
Si vous transformez une fonctionnalité de manière à modifier son échelle, vous devriez également essayer de la normaliser. Normaliser les données après la transformation peut améliorer les performances du modèle. Pour en savoir plus, consultez la section Données numériques: normalisation.
Un concept associé aux données catégorielles est le croisement de caractéristiques, qui synthétise le plus souvent deux caractéristiques différentes.