कभी-कभी, जब एमएल प्रैक्टिशनर को डोमेन की जानकारी होती है, तो इससे पता चलता है कि एक वैरिएबल, दूसरे वैरिएबल के स्क्वेयर, क्यूब या किसी दूसरी पावर से जुड़ा है. ऐसे में, मौजूदा संख्यात्मक वैल्यू में से किसी एक से सिंथेटिक वैल्यू बनाई जा सकती है.
यहां दिए गए डेटा पॉइंट के स्पैड पर ध्यान दें. यहां गुलाबी रंग के गोले, एक क्लास या कैटगरी (उदाहरण के लिए, पेड़ की एक प्रजाति) और हरे रंग के त्रिकोण, दूसरी क्लास (या पेड़ की दूसरी प्रजाति) को दिखाते हैं:
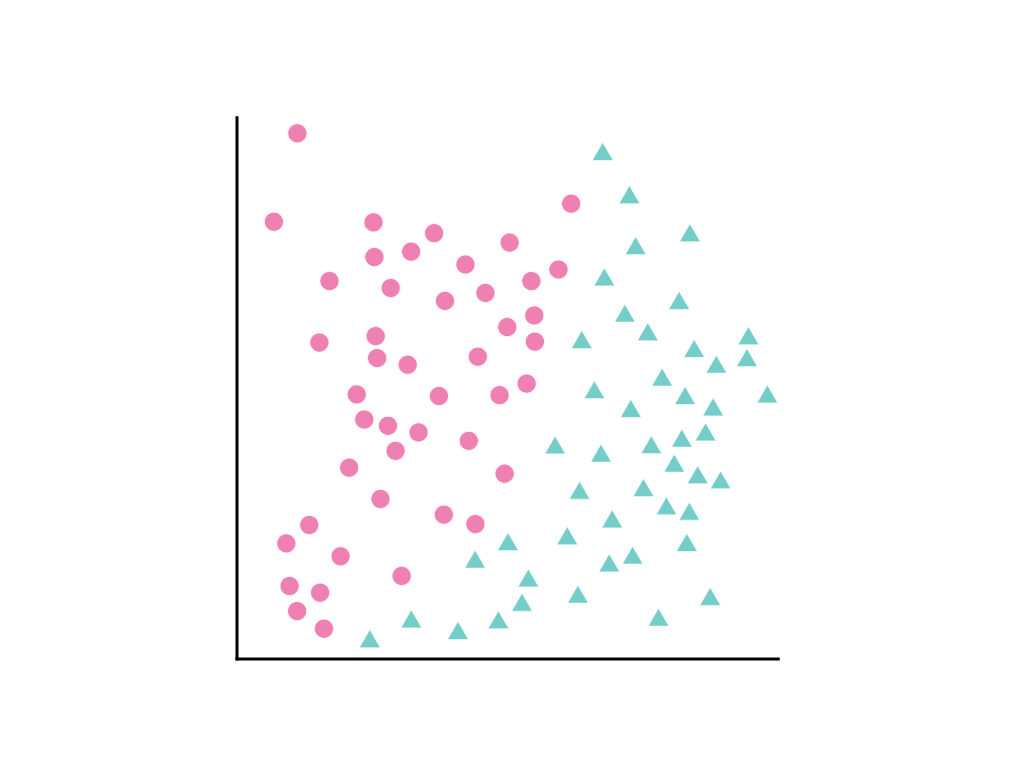
ऐसी सीधी रेखा नहीं खींची जा सकती जो दोनों क्लास को साफ़ तौर पर अलग करती हो. हालांकि, ऐसा कर सकने वाला कर्व खींचा जा सकता है:
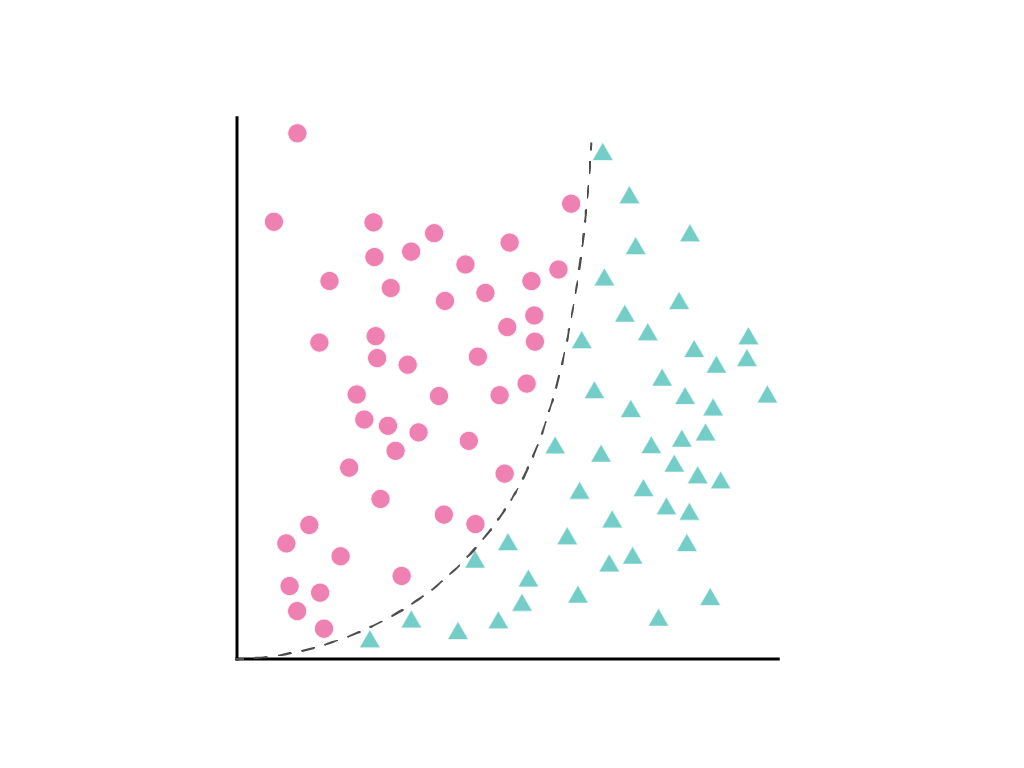
लीनियर रिग्रेशन मॉड्यूल में बताए गए तरीके के मुताबिक, एक फ़ीचर, $x_1$ वाले लीनियर मॉडल को लीनियर समीकरण से दिखाया जाता है:
अन्य सुविधाओं को, शर्तों \(w_2x_2\),\(w_3x_3\)वगैरह को जोड़कर मैनेज किया जाता है.
ग्रेडिएंट डिसेंट, वज़न $w_1$ (या अतिरिक्त सुविधाओं के मामले में, वज़न\(w_1\), \(w_2\), \(w_3\)) ढूंढता है, जो मॉडल के लॉस को कम करता है. हालांकि, दिखाए गए डेटा पॉइंट को लाइन से अलग नहीं किया जा सकता. मैं क्या करूं?
रैखिक समीकरण और नॉन-लाइनियरिटी,दोनों को एक साथ बनाए रखने के लिए, \(x_2\)नाम का नया शब्द तय करें. यह \(x_1\) का स्क्वेयर होता है:
इस सिंथेटिक सुविधा को पॉलीनोम ट्रांसफ़ॉर्म कहा जाता है. इसे किसी भी दूसरी सुविधा की तरह ही माना जाता है. पिछला लीनियर फ़ॉर्मूला इस तरह दिखेगा:
इसे अब भी लीनियर रिग्रेशन वाली समस्या के तौर पर माना जा सकता है. साथ ही, इसमें मौजूद स्क्वेयर किए गए 'टर्म' और पॉलीनोम ट्रांसफ़ॉर्म के बावजूद, वैल्यू को ग्रेडिएंट डिसेंट की मदद से तय किया जाता है. पॉलीनोमियल ट्रांसफ़ॉर्म को जोड़ने से, रैखिक मॉडल को ट्रेन करने के तरीके में कोई बदलाव किए बिना, मॉडल को $y = b + w_1x + w_2x^2$ फ़ॉर्म के कर्व का इस्तेमाल करके, डेटा पॉइंट को अलग करने की अनुमति मिलती है.
आम तौर पर, दिलचस्पी की संख्यात्मक वैल्यू को उसी संख्या से गुणा किया जाता है, यानी कि किसी घात में रखा जाता है. कभी-कभी, एमएल विशेषज्ञ सही एक्सपोनेंट के बारे में अनुमान लगा सकता है. उदाहरण के लिए, दुनिया में कई रिलेशनशिप, स्क्वेयर किए गए शब्दों से जुड़ी होती हैं. इनमें गुरुत्वाकर्षण की वजह से होने वाला त्वरण, दूरी के हिसाब से रोशनी या आवाज़ का कम होना, और इलास्टिक संभावित ऊर्जा शामिल है.
अगर किसी एट्रिब्यूट को इस तरह बदला जाता है कि उसका स्केल बदल जाता है, तो आपको उसे सामान्य बनाने के लिए भी प्रयोग करना चाहिए. डेटा को ट्रांसफ़ॉर्म करने के बाद, उसे सामान्य बनाने से मॉडल की परफ़ॉर्मेंस बेहतर हो सकती है. ज़्यादा जानकारी के लिए, न्यूमेरिकल डेटा: नॉर्मलाइज़ेशन देखें.
कैटगरी वाले डेटा से जुड़ा एक कॉन्सेप्ट, फ़ीचर क्रॉस है. यह अक्सर दो अलग-अलग फ़ीचर को सिंथेसाइज़ करता है.
