Иногда, когда у специалиста по МО есть знания предметной области, предполагающие, что одна переменная связана с квадратом, кубом или другой степенью другой переменной, полезно создать синтетический признак на основе одного из существующих числовых признаков .
Рассмотрим следующий набор точек данных, где розовые кружки представляют один класс или категорию (например, породу дерева), а зеленые треугольники — другой класс (или породу дерева):
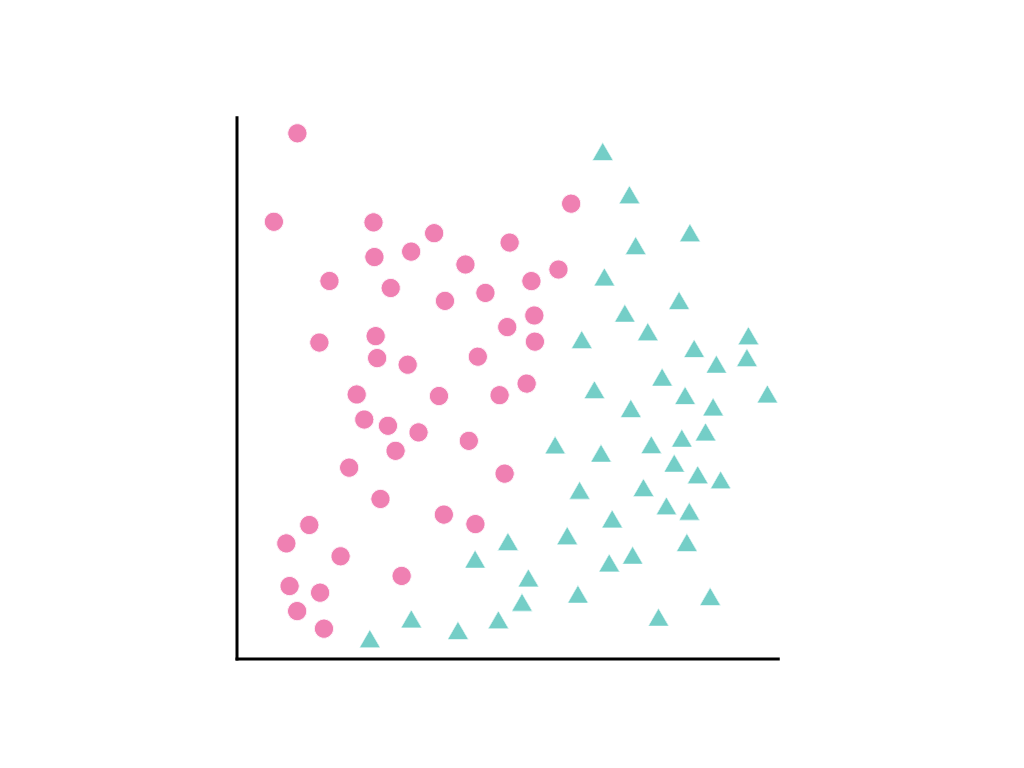
Невозможно провести прямую линию, которая четко разделяет два класса, но можно нарисовать кривую, которая делает это:
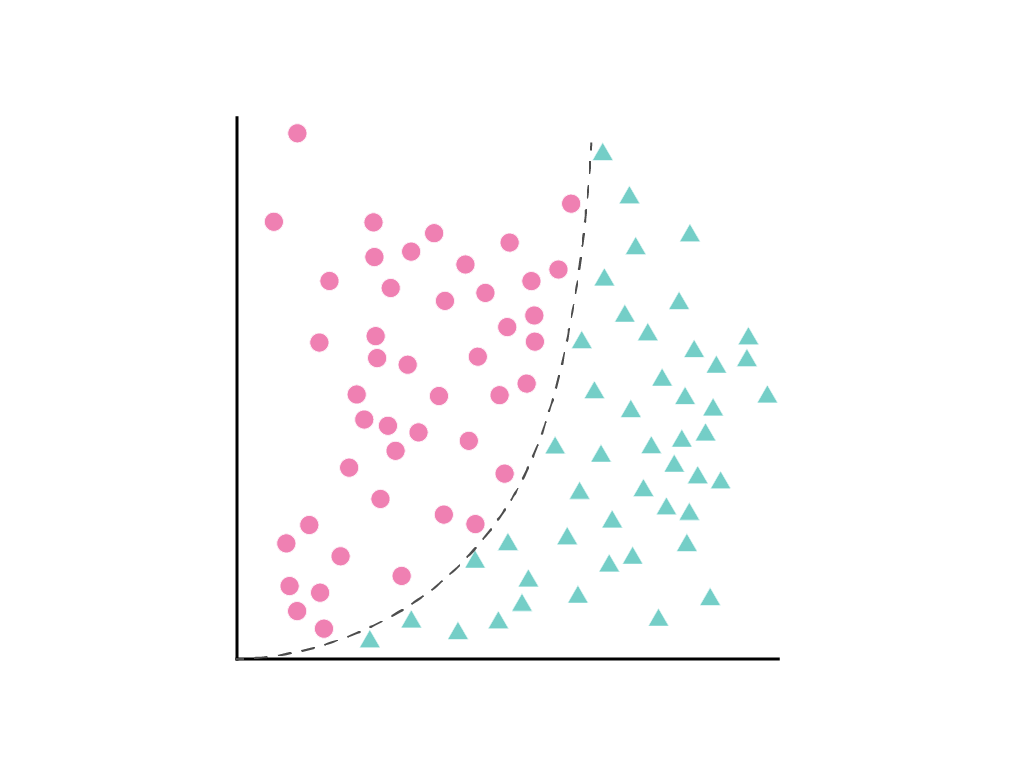
Как обсуждалось в модуле «Линейная регрессия» , линейная модель с одним признаком $x_1$ описывается линейным уравнением:
Дополнительные функции реализуются путем добавления терминов. \(w_2x_2\),\(w_3x_3\), и т. д.
Градиентный спуск находит вес $w_1$ (или веса\(w_1\), \(w_2\), \(w_3\), в случае дополнительных функций), что минимизирует потери модели. Но показанные точки данных не могут быть разделены линией. Что можно сделать?
Можно сохранить как линейное уравнение , так и разрешить нелинейность, определив новый термин: \(x_2\), это просто \(x_1\) в квадрате:
Эта синтетическая функция, называемая полиномиальным преобразованием, рассматривается как любая другая функция. Предыдущая линейная формула принимает вид:
Это по-прежнему можно рассматривать как задачу линейной регрессии , а веса, как обычно, определяются посредством градиентного спуска, несмотря на то, что они содержат скрытый квадратичный член, полиномиальное преобразование. Не изменяя способ обучения линейной модели, добавление полиномиального преобразования позволяет модели разделять точки данных с помощью кривой вида $y = b + w_1x + w_2x^2$.
Обычно интересующий числовой признак умножается сам на себя, то есть возводится в некоторую степень. Иногда специалист по МО может сделать обоснованное предположение о соответствующем показателе. Например, многие отношения в физическом мире связаны с квадратами, включая ускорение силы тяжести, затухание света или звука на расстоянии и упругую потенциальную энергию.
Родственной концепцией в категориальных данных является перекрестный признак , который чаще всего синтезирует два разных признака.