บางครั้งเมื่อผู้ปฏิบัติงาน ML มีความรู้ในโดเมนที่ชี้ว่าตัวแปรหนึ่งเกี่ยวข้องกับการคูณด้วย 2 คูณด้วย 2, คูณด้วย 3 หรือกำลังอื่นๆ ของตัวแปรอื่น ก็ควรสร้างฟีเจอร์สังเคราะห์จากฟีเจอร์เชิงตัวเลขที่มีอยู่
พิจารณาการกระจายจุดข้อมูลต่อไปนี้ โดยวงกลมสีชมพูแสดงถึงคลาสหรือหมวดหมู่หนึ่ง (เช่น สายพันธุ์ของต้นไม้) และสามเหลี่ยมสีเขียวแสดงถึงอีกคลาสหนึ่ง (หรือสายพันธุ์ของต้นไม้)
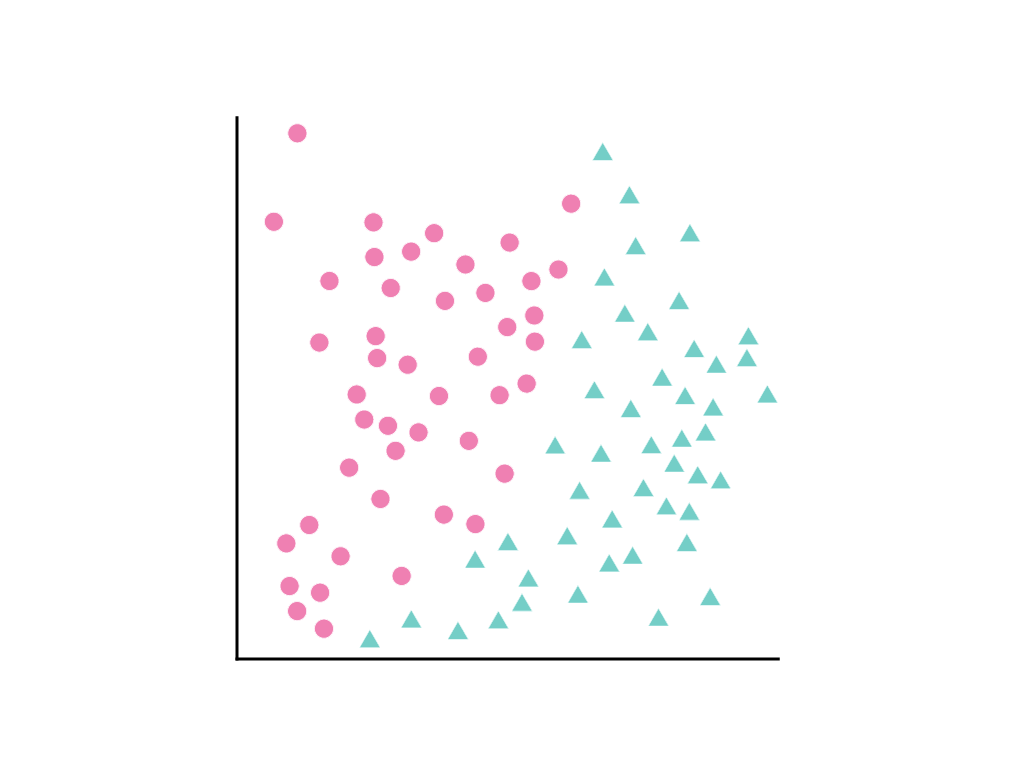
คุณจะวาดเส้นตรงที่แยกคลาส 2 คลาสนี้ได้อย่างเรียบร้อยไม่ได้ แต่สามารถวาดเส้นโค้งที่แยกคลาส 2 คลาสนี้
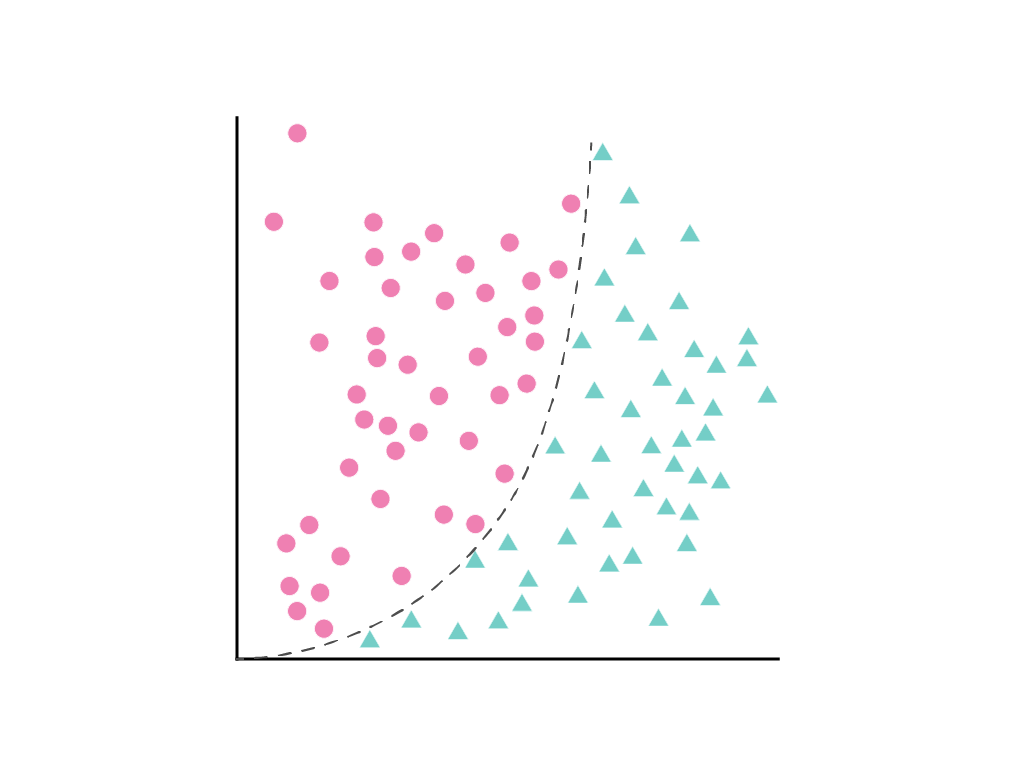
ดังที่ได้กล่าวไว้ในโมดูลการถดถอยเชิงเส้น รูปแบบเชิงเส้นที่มี 1 ฟีเจอร์ $x_1$ จะอธิบายด้วยสมการเชิงเส้นดังนี้
ฟีเจอร์เพิ่มเติมจะจัดการโดยการเพิ่มข้อกำหนด \(w_2x_2\) \(w_3x_3\)ฯลฯ
การลดค่าการลาดชันจะค้นหาน้ำหนัก $w_1$ (หรือน้ำหนัก \(w_1\), \(w_2\), \(w_3\)ในกรณีที่มีฟีเจอร์เพิ่มเติม) ที่ลดการสูญเสียของโมเดลได้น้อยที่สุด แต่จุดข้อมูลที่แสดงต้องไม่แยกด้วยเส้น ฉันต้องทำอย่างไร
คุณสามารถเก็บทั้งสมการเชิงเส้นไว้และอนุญาตลักษณะที่ไม่ใช่เชิงเส้นได้ โดยกำหนดคำใหม่ \(x_2\)ที่เป็นเพียงแค่ \(x_1\) ยกกำลัง 2 ดังนี้
ระบบจะถือว่าองค์ประกอบสังเคราะห์นี้ซึ่งเรียกว่าการเปลี่ยนรูปแบบพหุนามเหมือนกับองค์ประกอบอื่นๆ สูตรเชิงเส้นก่อนหน้านี้จะเปลี่ยนเป็น
ปัญหานี้ยังคงได้รับการพิจารณาว่าเป็นปัญหาการประมาณเชิงเส้น และน้ำหนักจะกำหนดผ่านการถดถอยเชิงกริดตามปกติ แม้ว่าจะมีเทอมที่ยกกำลัง 2 ที่ซ่อนอยู่ ซึ่งเป็นการเปลี่ยนรูปแบบพหุนาม การเพิ่มการเปลี่ยนรูปแบบพหุนามช่วยให้โมเดลแยกจุดข้อมูลโดยใช้เส้นโค้งของรูปแบบ $y = b + w_1x + w_2x^2$ ได้โดยไม่ต้องเปลี่ยนวิธีฝึกโมเดลเชิงเส้น
โดยทั่วไป ฟีเจอร์ตัวเลขที่น่าสนใจจะคูณด้วยตัวมันเอง ซึ่งก็คือการยกกำลัง บางครั้งผู้ปฏิบัติงานด้าน ML อาจเดาค่าที่ยกกำลังที่เหมาะสมได้ ตัวอย่างเช่น ความสัมพันธ์หลายอย่างในโลกกายภาพเกี่ยวข้องกับคำยกกำลัง 2 ซึ่งรวมถึงความเร่งเนื่องจากแรงโน้มถ่วง การลดทอนแสงหรือเสียงตามระยะทาง และพลังงานศักย์แบบยืดหยุ่น
หากคุณเปลี่ยนรูปแบบองค์ประกอบในลักษณะที่เปลี่ยนมาตราส่วน คุณควรลองใช้การปรับให้เป็นมาตรฐานด้วย การทำให้เป็นมาตรฐานหลังจากการเปลี่ยนรูปแบบอาจทําให้โมเดลทํางานได้ดีขึ้น ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลตัวเลข: การทำให้ค่าเป็นมาตรฐาน
แนวคิดที่เกี่ยวข้องในข้อมูลเชิงหมวดหมู่คือการครอสฟีเจอร์ ซึ่งจะสังเคราะห์ฟีเจอร์ 2 รายการที่แตกต่างกันบ่อยครั้ง