Terkadang, jika praktisi ML memiliki pengetahuan domain yang menunjukkan bahwa satu variabel terkait dengan kuadrat, kubus, atau pangkat lain dari variabel lain, sebaiknya buat fitur sintetis dari salah satu fitur numerik yang ada.
Pertimbangkan penyebaran titik data berikut, dengan lingkaran merah muda mewakili satu kelas atau kategori (misalnya, spesies pohon) dan segitiga hijau kelas lain (atau spesies pohon):
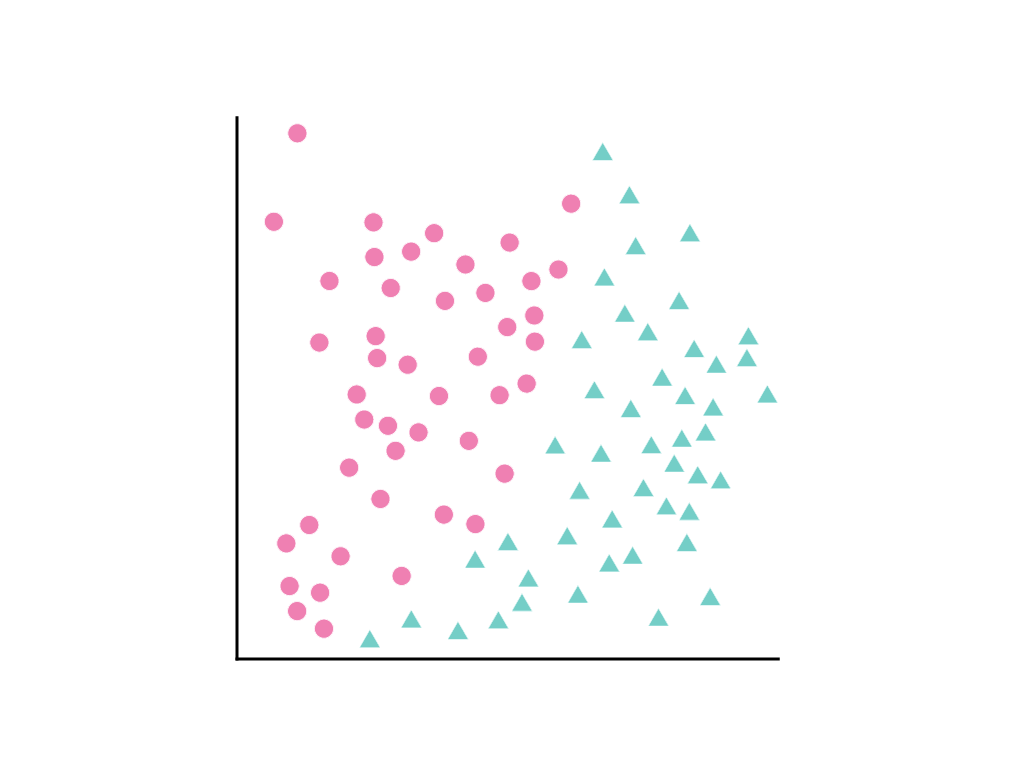
Anda tidak dapat menggambar garis lurus yang memisahkan kedua class dengan jelas, tetapi dapat menggambar kurva yang melakukannya:
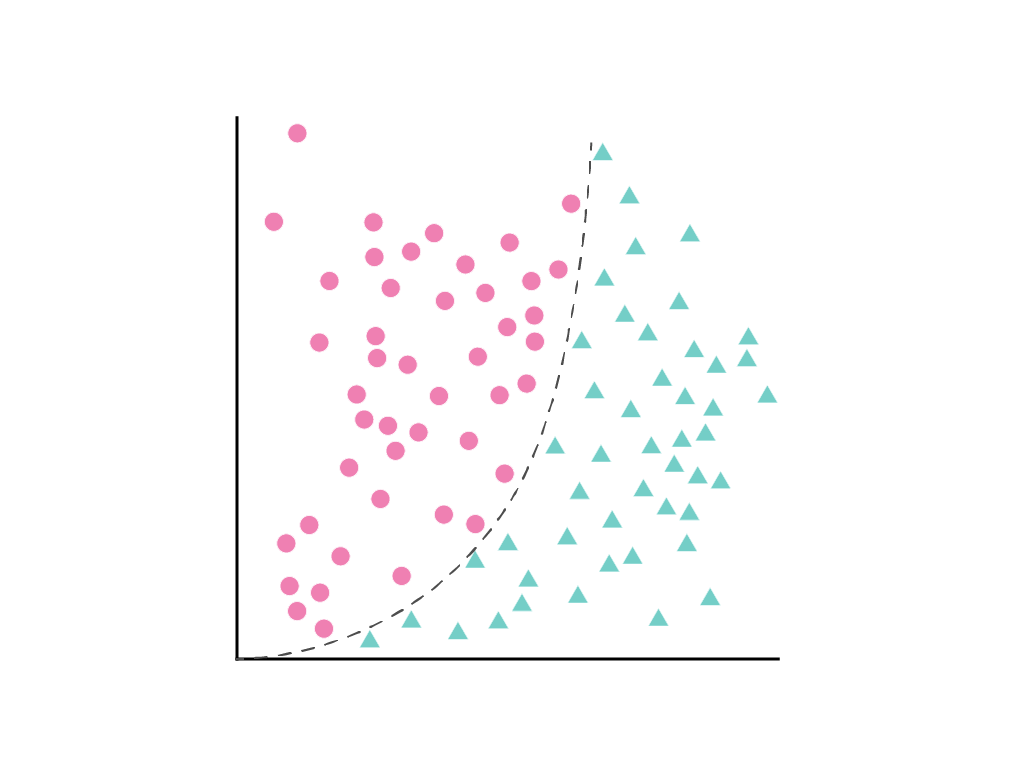
Seperti yang dibahas dalam Modul regresi linear, model linear dengan satu fitur, $x_1$, dijelaskan oleh persamaan linear:
Fitur tambahan ditangani dengan penambahan istilah \(w_2x_2\), \(w_3x_3\), dll.
Penurunan gradien menemukan bobot $w_1$ (atau bobot \(w_1\), \(w_2\), \(w_3\), dalam kasus fitur tambahan) yang meminimalkan penyimpangan model. Namun, titik data yang ditampilkan tidak dapat dipisahkan oleh garis. Apa yang dapat dilakukan?
Anda dapat mempertahankan persamaan linear dan mengizinkan nonlinearitas dengan menentukan istilah baru, \(x_2\), yang merupakan \(x_1\) kuadrat:
Fitur sintetis ini, yang disebut transformasi polinomial, diperlakukan seperti fitur lainnya. Rumus linear sebelumnya menjadi:
Hal ini masih dapat diperlakukan seperti masalah regresi linear, dan bobot ditentukan melalui gradien turun, seperti biasa, meskipun berisi istilah kuadrat tersembunyi, transformasi polinomial. Tanpa mengubah cara model linier dilatih, penambahan transformasi polinomial memungkinkan model memisahkan titik data menggunakan kurva bentuk $y = b + w_1x + w_2x^2$.
Biasanya, fitur numerik yang diminati dikalikan dengan dirinya sendiri, yaitu diangkat ke beberapa pangkat. Terkadang, praktisi ML dapat membuat tebakan yang tepat tentang eksponen yang sesuai. Misalnya, banyak hubungan di dunia fisik terkait dengan istilah kuadrat, termasuk akselerasi karena gravitasi, pelemahan cahaya atau suara dari jarak, dan energi potensial elastis.
Jika Anda mengubah fitur dengan cara yang mengubah skalanya, Anda juga harus mempertimbangkan untuk melakukan eksperimen dengan menormalisasinya. Normalisasi setelah melakukan transformasi mungkin akan membuat model berperforma lebih baik. Untuk informasi selengkapnya, lihat Data Numerik: Normalisasi.
Konsep terkait dalam data kategoris adalah silang fitur, yang lebih sering menyintesis dua fitur yang berbeda.
