A volte, quando l'esperto di ML ha conoscenze del dominio che suggeriscono che una variabile è correlata al quadrato, al cubo o ad altre potenze di un'altra variabile, è utile creare un'caratteristica sintetica da una delle caratteristiche numeriche esistenti.
Considera la seguente distribuzione dei punti dati, in cui i cerchi rosa rappresentano una classe o una categoria (ad esempio una specie di albero) e i triangoli verdi un'altra classe (o specie di albero):
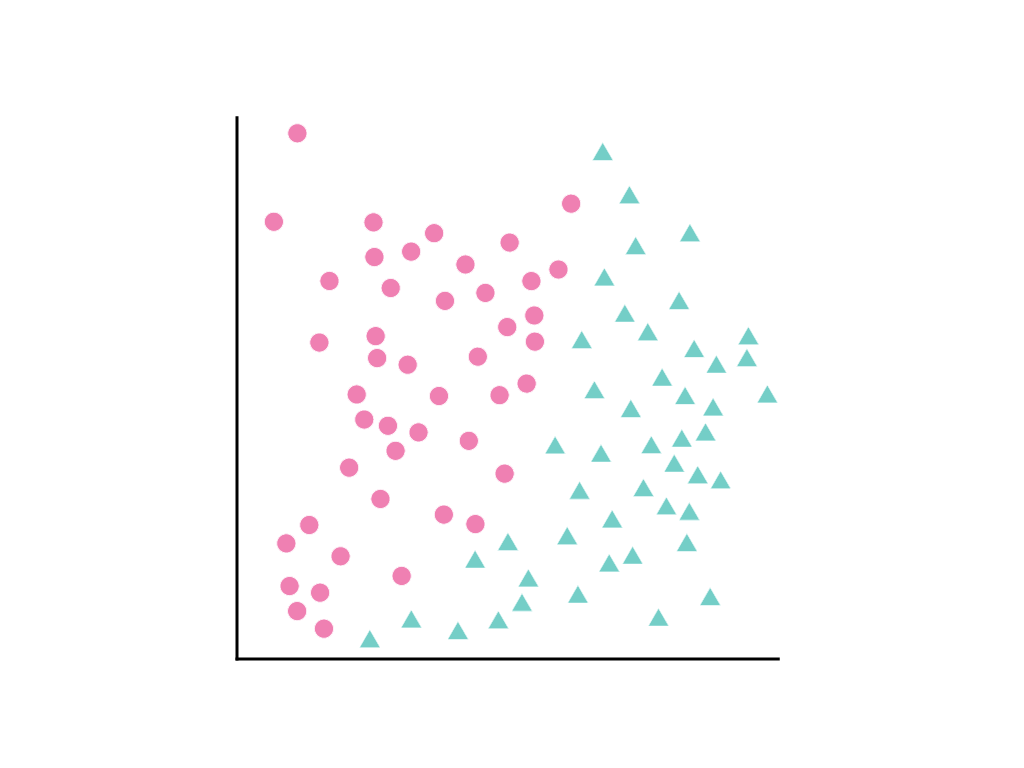
Non è possibile disegnare una linea retta che separi nettamente le due classi, ma è possibile disegnare una curva che lo faccia:
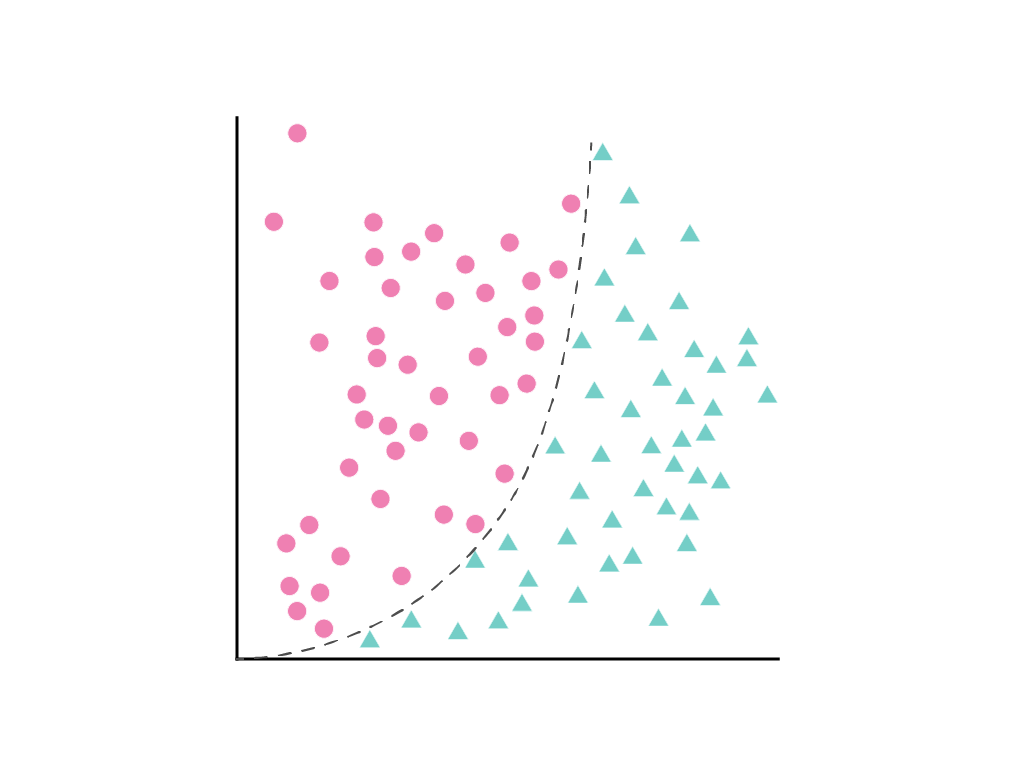
Come discusso nel modulo sulla regressione lineare, un modello lineare con una caratteristica, $x_1$, è descritto dall'equazione lineare:
Le funzionalità aggiuntive vengono gestite aggiungendo i termini \(w_2x_2\), \(w_3x_3\)e così via.
La discesa del gradiente trova il peso $w_1$ (o i pesi \(w_1\), \(w_2\), \(w_3\), nel caso di funzionalità aggiuntive) che minimizza la perdita del modello. Tuttavia, i punti dati mostrati non possono essere separati da una linea. Che cosa posso fare?
È possibile mantenere sia l'equazione lineare che consentire la non linearità definendo un nuovo termine, \(x_2\), che è semplicemente \(x_1\) al quadrato:
Questa caratteristica sintetica, chiamata trasformazione polinomiale, viene trattata come qualsiasi altra caratteristica. La formula lineare precedente diventa:
Questo può comunque essere trattato come un problema di regressione lineare e i pesi determinati tramite la discesa del gradiente, come di consueto, nonostante contenga un termine quadrato nascosto, la trasformazione polinomiale. Senza modificare il modo in cui viene addestrato il modello lineare, l'aggiunta di una trasformazione polinomiale consente al modello di separare i punti dati utilizzando una curva della forma $y = b + w_1x + w_2x^2$.
In genere, la caratteristica numerica di interesse viene moltiplicata per se stessa, ovvero viene elevata a una certa potenza. A volte un professionista del machine learning può fare un'ipotesi informata sull'esponente appropriato. Ad esempio, molte relazioni nel mondo fisico sono correlate a termini al quadrato, tra cui l'accelerazione dovuta alla gravità, l'attenuazione della luce o del suono in base alla distanza e l'energia potenziale elastica.
Se trasformi una funzionalità in modo da modificarne la scala, ti consigliamo di provare anche a normalizzarla. La normalizzazione dopo la trasformazione potrebbe migliorare il rendimento del modello. Per ulteriori informazioni, consulta la pagina Dati numerici: normalizzazione.
Un concetto correlato nei dati categorici è il incrocio di caratteristiche, che più frequentemente sintetizza due diverse caratteristiche.