گاهی اوقات، زمانی که متخصص ML دارای دانش دامنه ای است که نشان می دهد یک متغیر با مربع، مکعب یا قدرت دیگر متغیر دیگر مرتبط است، ایجاد یک ویژگی ترکیبی از یکی از ویژگی های عددی موجود مفید است.
گسترش نقاط داده زیر را در نظر بگیرید، که در آن دایره های صورتی یک طبقه یا دسته (به عنوان مثال، گونه ای از درخت) را نشان می دهند و مثلث های سبز یک کلاس دیگر (یا گونه های درخت) را نشان می دهند:
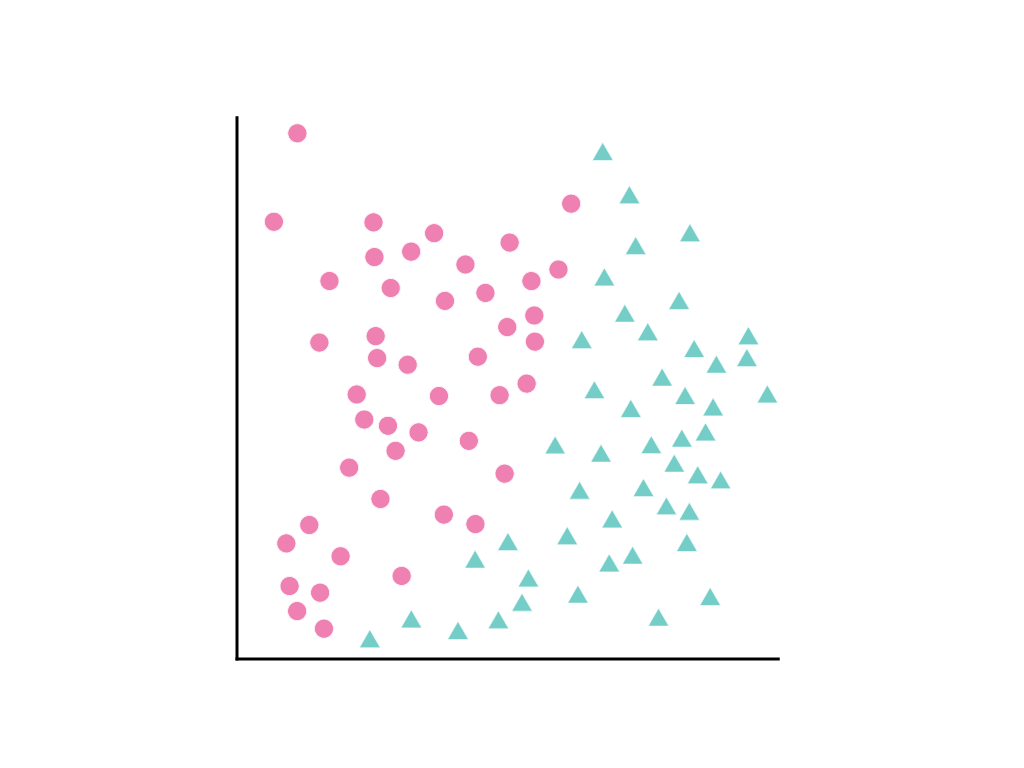
نمی توان یک خط مستقیم رسم کرد که دو کلاس را به طور تمیز از هم جدا کند، اما می توان منحنی را ترسیم کرد که این کار را انجام دهد:
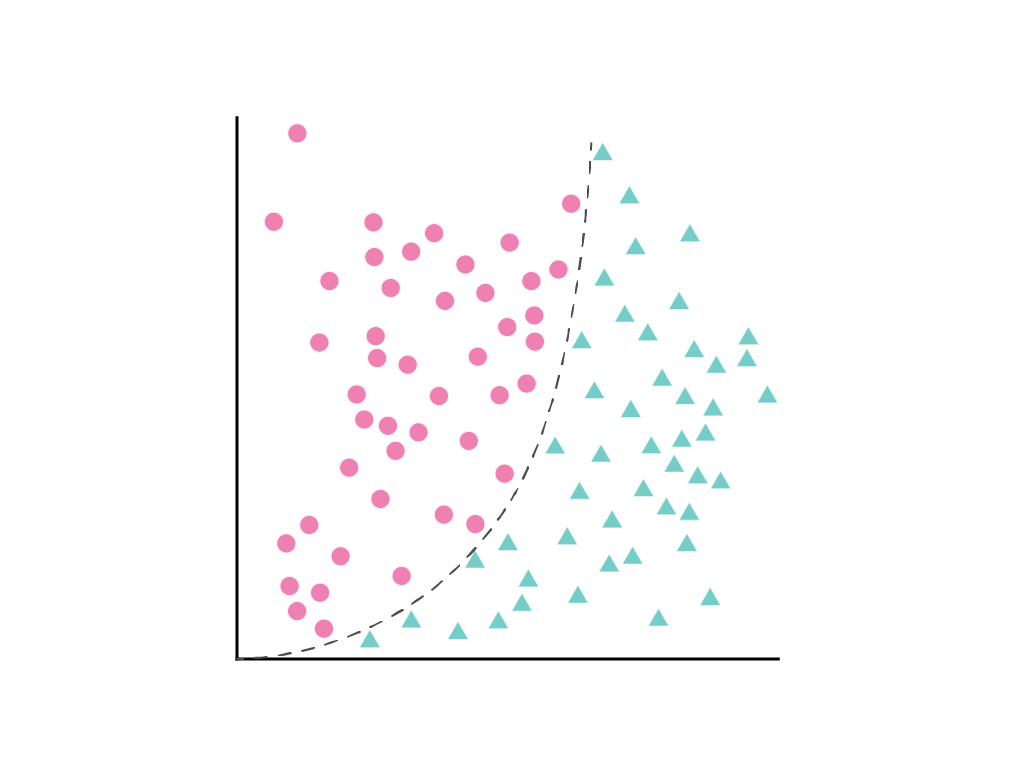
همانطور که در ماژول رگرسیون خطی بحث شد، یک مدل خطی با یک ویژگی، $x_1$، با معادله خطی توصیف می‌شود:
ویژگی‌های اضافی با اضافه کردن شرایط انجام می‌شود \(w_2x_2\)،\(w_3x_3\)و غیره
نزول گرادیان وزن $w_1$ (یا وزن ها را پیدا می کند\(w_1\)، \(w_2\)، \(w_3\)، در مورد ویژگی های اضافی) که از دست دادن مدل را به حداقل می رساند. اما نقاط داده نشان داده شده را نمی توان با یک خط جدا کرد. چه کاری می توان کرد؟
می توان معادله خطی را حفظ کرد و با تعریف یک عبارت جدید اجازه غیرخطی بودن را داد. \(x_2\)، این به سادگی است \(x_1\) مربع:
این ویژگی مصنوعی که تبدیل چند جمله ای نامیده می شود، مانند هر ویژگی دیگری در نظر گرفته می شود. فرمول خطی قبلی به صورت زیر می شود:
این هنوز هم می‌تواند مانند یک مسئله رگرسیون خطی باشد و وزن‌ها از طریق نزول گرادیان، طبق معمول، با وجود یک عبارت مربع پنهان، تبدیل چند جمله‌ای، تعیین شوند. بدون تغییر نحوه آموزش مدل خطی، افزودن یک تبدیل چند جمله ای به مدل اجازه می دهد تا نقاط داده را با استفاده از منحنی به شکل $y = b + w_1x + w_2x^2$ جدا کند.
معمولاً ویژگی عددی علاقه در خودش ضرب می شود، یعنی به مقداری توان بالا می رود. گاهی اوقات یک متخصص ML می تواند در مورد توان مناسب حدس بزند. به عنوان مثال، بسیاری از روابط در دنیای فیزیکی به عبارات مربع مربوط می شود، از جمله شتاب ناشی از گرانش، تضعیف نور یا صدا در فاصله، و انرژی پتانسیل الاستیک.
یک مفهوم مرتبط در داده های طبقه بندی شده ، متقاطع ویژگی است که بیشتر دو ویژگی متفاوت را ترکیب می کند.