לפעמים, כשלמומחה ה-ML יש ידע בתחום שמצביע על כך שמשתנה אחד קשור למשתנה אחר בריבועים, בחזקה שלישית או בחזקה אחרת, כדאי ליצור תכונה סינתטית מאחד מהמאפיינים המספריים הקיימים.
עיינו בהתפלגות של נקודות הנתונים הבאה, שבה עיגולים ורודים מייצגים סיווג או קטגוריה אחת (לדוגמה, מין של עץ) ומשולשים ירוקים מייצגים סיווג אחר (או מין אחר של עץ):
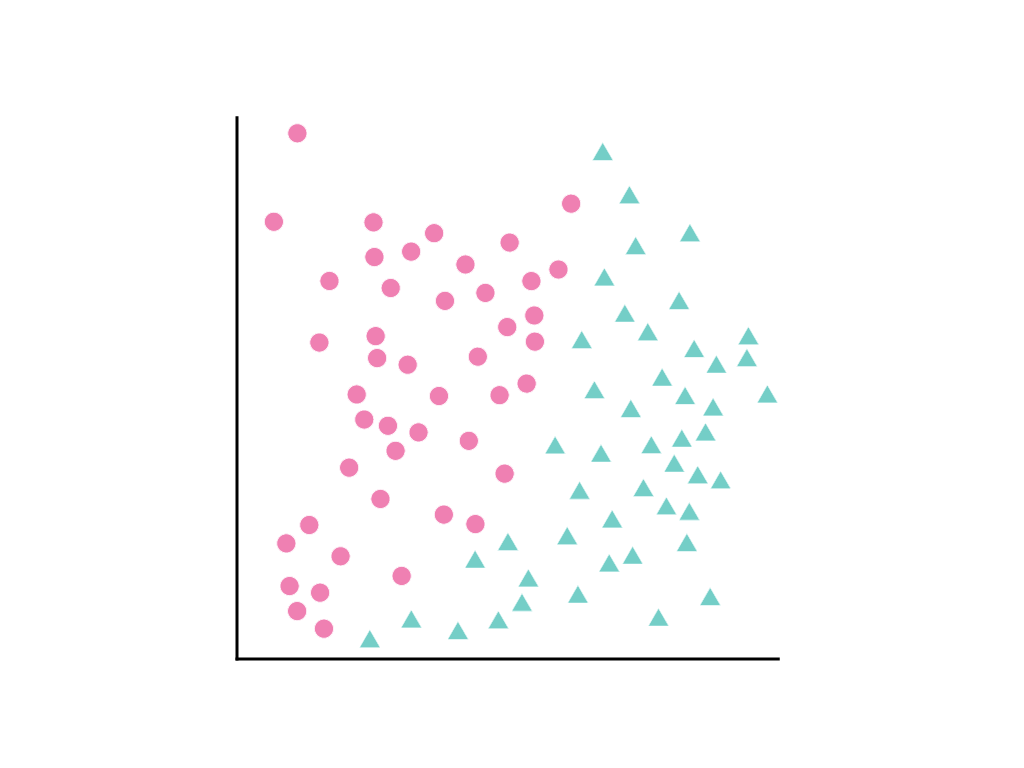
אי אפשר לצייר קו ישר שמפריד בבירור בין שתי הכיתות, אבל אפשר לצייר עקומה שמפרידה בבירור:
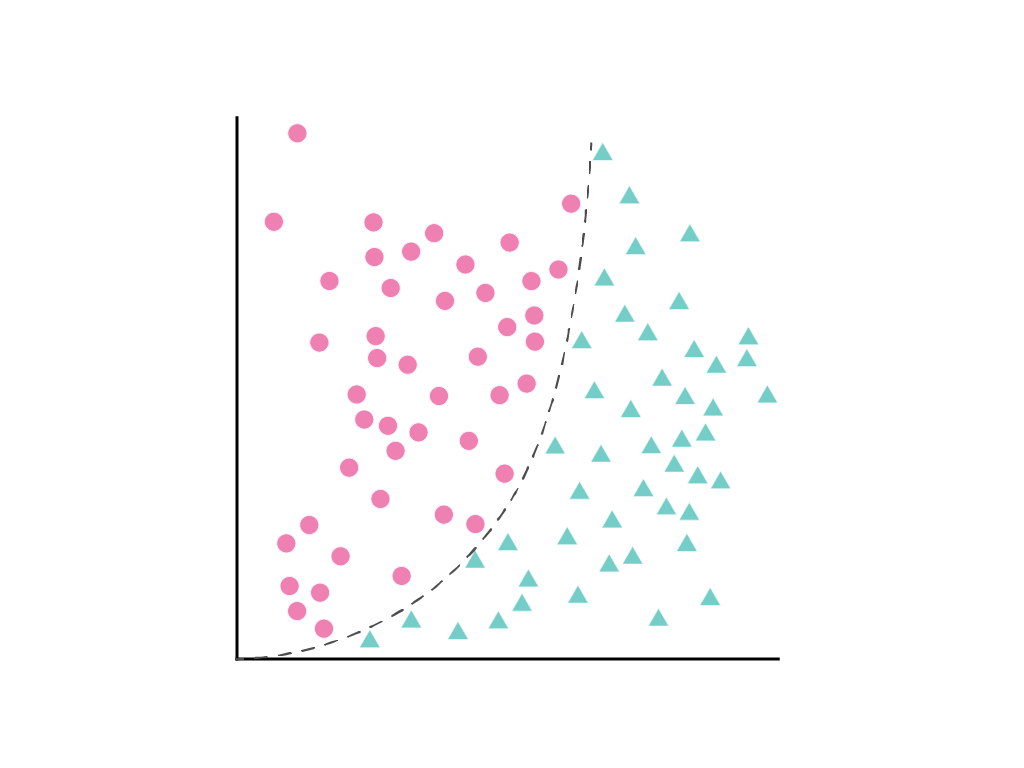
כפי שצוין במודול 'רגרסיה לינארית', מודל לינארי עם מאפיין אחד, $x_1$, מתואר באמצעות המשוואה הליניארית:
כדי להוסיף תכונות, מוסיפים את המונחים \(w_2x_2\),\(w_3x_3\)וכו'.
ירידה בגרדינט מאתרת את המשקל $w_1$ (או את המשקלים\(w_1\), \(w_2\), \(w_3\), במקרה של תכונות נוספות) שמקטין את אובדן המודל. אבל לא ניתן להפריד בין נקודות הנתונים המוצגות באמצעות קו. מה אוכל לעשות?
אפשר לשמור על המשוואה הליניארית וגם לאפשר פונקציה לא לינארית על ידי הגדרת ביטוי חדש, \(x_2\), שהוא פשוט \(x_1\) בחזקת 2:
התכונה הסינתטית הזו, שנקראת טרנספורמציה פולינומית, מטופלת כמו כל תכונה אחרת. הנוסחה הליניארית הקודמת הופכת ל:
עדיין אפשר להתייחס לבעיה הזו כאל בעיה של רגרסיה לינארית, והמשקלים נקבעים באמצעות ירידה בגרדינט, כרגיל, למרות שהם מכילים מונח ריבוע מוסתר, הטרנספורמציה הפולינומית. בלי לשנות את אופן האימון של המודל הליניארי, הוספת טרנספורמציה פולינומית מאפשרת למודל להפריד בין נקודות הנתונים באמצעות עקומה מהצורה $y = b + w_1x + w_2x^2$.
בדרך כלל, המאפיין המספרי הרצוי מוכפל בעצמו, כלומר מוגבה בחזקה כלשהי. לפעמים מומחה ב-ML יכול להעריך בצורה מושכלת את החזקה המתאימה. לדוגמה, הרבה יחסי גומלין בעולם הפיזי קשורים לביטויים ריבועיים, כולל האצה עקב כוח הכבידה, דעיכת האור או הצליל במרחק ואנרגיה פוטנציאלית אלסטית.
אם אתם מבצעים טרנספורמציה של מאפיין באופן שמשנה את קנה המידה שלו, כדאי לנסות גם לבצע נורמליזציה שלו. נורמליזציה אחרי טרנספורמציה עשויה לשפר את הביצועים של המודל. מידע נוסף זמין במאמר נתונים מספריים: נורמליזציה.
מושג קשור בנתונים קטגוריאליים הוא מיזוג תכונות, שמכיל לרוב סינתזה של שתי תכונות שונות.