Іноді, коли фахівець із машинного навчання володіє галузевими знаннями, які дають змогу припустити, що одна змінна пов’язана з іншою, піднесеною до степеня (такого як квадрат, куб тощо), корисно створити синтетичну ознаку на основі однієї з наявних числових ознак.
Розгляньмо розподіл точок даних, наведений нижче. Тут рожевими колами позначено один клас чи категорію (наприклад, вид дерева), а зеленими трикутниками – інший клас (або вид дерева):
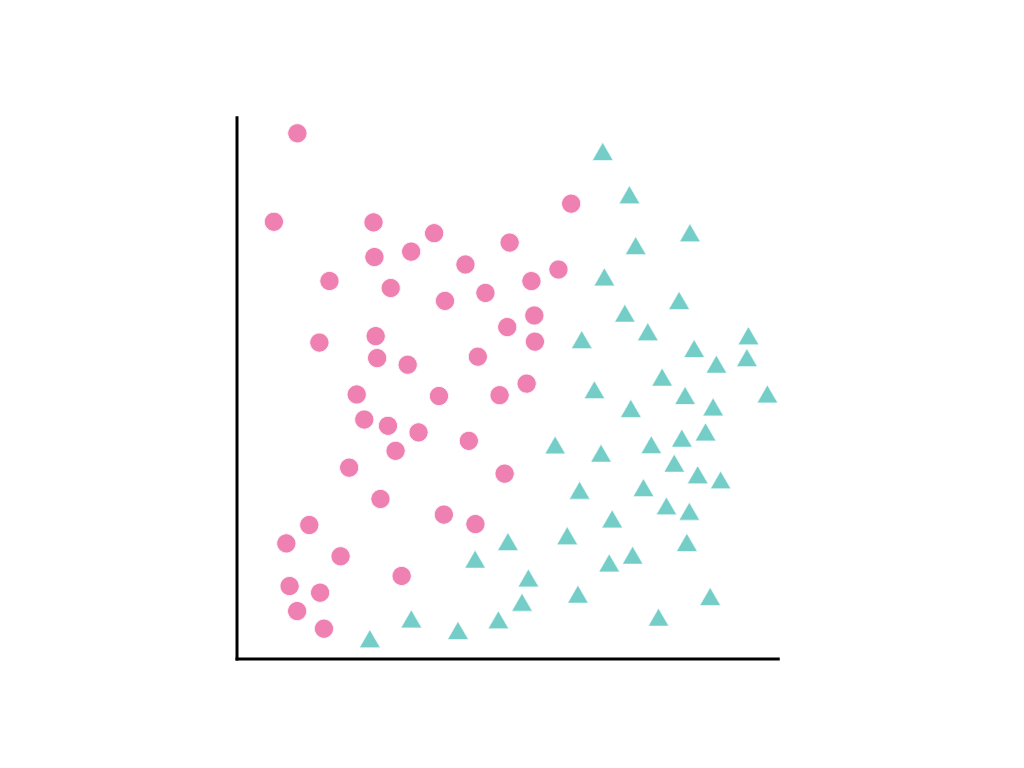
Неможливо провести пряму лінію, яка б чітко розділяла ці два класи, але можна зробити це кривою:
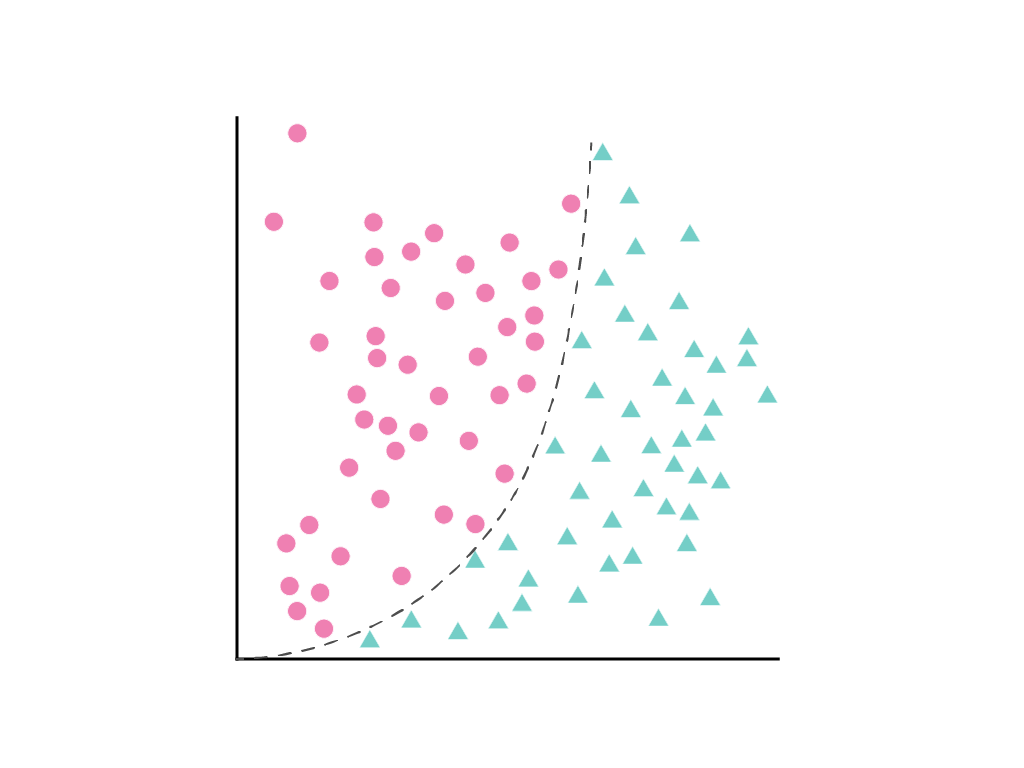
Як зазначалося в модулі Лінійна регресія, лінійну модель з однією ознакою ($x_1$) виражає лінійне рівняння:
Інші ознаки виражають, додаючи члени \(w_2x_2\),\(w_3x_3\)тощо).
Градієнтний спуск знаходить вагу $w_1$ (або\(w_1\), \(w_2\), \(w_3\), якщо є додаткові ознаки), що мінімізує втрату моделі. Але наведені точки даних не можна розділити прямою. Що робити?
Можливо як зберегти лінійне рівняння, так і допустити нелінійність, визначивши новий член, \(x_2\), який дорівнюватиме члену \(x_1\) , просто піднесеному до квадрата:
Ця синтетична ознака, яка називається поліноміальним перетворенням, обробляється так само, як і будь-яка інша. Попередня лінійна формула набуває такого вигляду:
Цю задачу все ще можна розглядати як задачу лінійної регресії, а ваги визначати за допомогою градієнтного спуску, як зазвичай, хоч вони й містять прихований квадратичний член, тобто поліноміальне перетворення. Якщо не змінювати спосіб навчання лінійної моделі, але додати поліноміальне перетворення, модель зможе розмежовувати точки даних за допомогою кривої вигляду $y = b + w_1x + w_2x^2$.
Зазвичай числову ознаку, яка нас цікавить, множать на неї саму, тобто підносять до певного степеня. Іноді спеціаліст із машинного навчання може зробити обґрунтоване припущення щодо відповідного показника степеня. Наприклад, через піднесення до квадрата виражено багато взаємозв’язків фізичного світу, зокрема прискорення під дією гравітації, загасання світла чи звуку зі збільшенням відстані або пружна потенційна енергія.
Споріднене поняття, пов’язане з категорійними даними, – це поєднання ознак, що частіше є синтезом двох різних ознак.