ML 担当者が、ある変数が別の変数の 2 乗、3 乗、その他のべき乗に関連していることを示すドメイン知識を持っている場合は、既存の数値特徴量のいずれかから合成特徴量を作成すると便利です。
次のデータポイントの分布について考えてみましょう。ピンクの円は 1 つのクラスまたはカテゴリ(木の種類など)を表し、緑色の三角形は別のクラス(または木の種類)を表します。
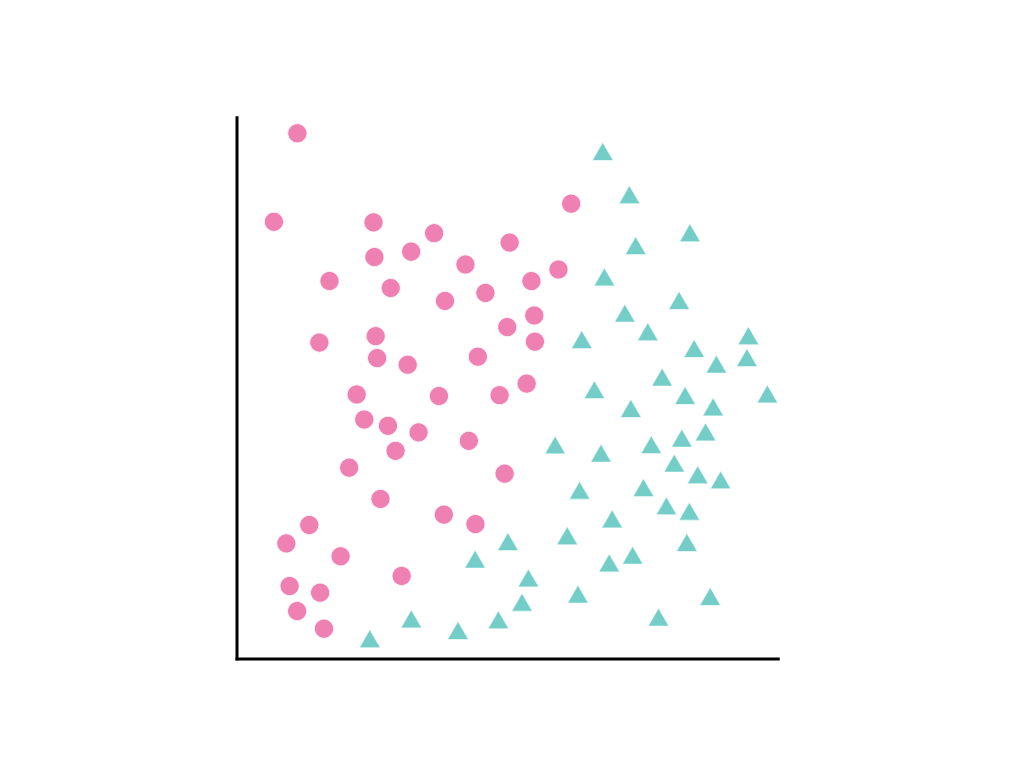
2 つのクラスを明確に分ける直線を引くことはできませんが、分ける曲線を引くことは可能です。
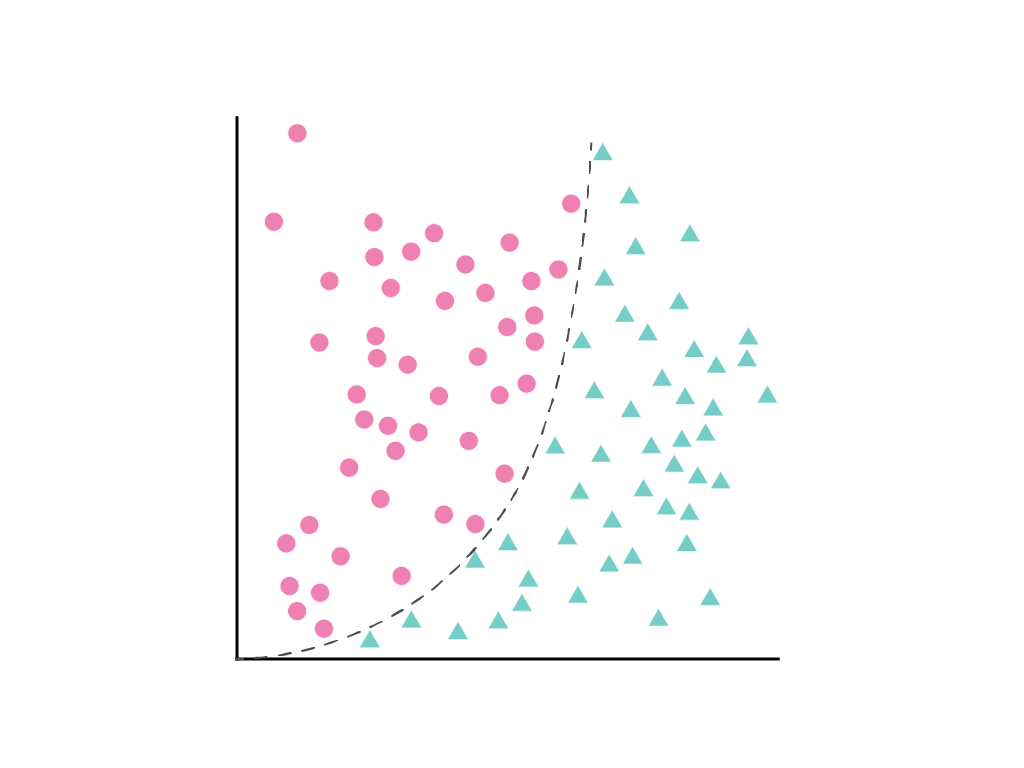
線形回帰モジュールで説明したように、1 つの特徴量 $x_1$ を持つ線形モデルは、次の線形方程式で表されます。
その他の機能は、 \(w_2x_2\)や\(w_3x_3\)などの用語を追加することで処理されます。
勾配降下は、モデルの損失を最小化する重み $w_1$(または追加の特徴量の場合は重み\(w_1\)、 \(w_2\)、 \(w_3\))を見つけます。ただし、表示されるデータポイントは線で区切ることができません。どうすればよいですか?
線形方程式と非線形性を両方とも維持するには、 \(x_1\) の 2 乗という新しい項 \(x_2\)を定義します。
この合成特徴(多項式変換)は、他の特徴と同様に扱われます。前の線形数式は次のようになります。
これは、隠れた平方項(多項式変換)が含まれていても、線形回帰問題として扱うことができ、重みは通常どおり勾配降下によって決定されます。多項式変換を追加すると、線形モデルのトレーニング方法を変更せずに、y = b + w_1x + w_2x^2 の形式の曲線を使用してデータポイントを分離できます。
通常、対象の数値特徴は自身に掛け合わされます。つまり、あるべき乗に上げられます。ML 担当者は、適切な指数について十分な情報に基づいて推測できる場合があります。たとえば、物理世界における多くの関係は、重力加速度、距離に応じた光や音の減衰、弾性ポテンシャル エネルギーなど、2 乗の項に関連しています。
スケールを変更する方法で特徴を変換する場合は、正規化も試してみることを検討してください。変換後に正規化すると、モデルのパフォーマンスが向上する場合があります。詳細については、数値データ: 正規化をご覧ください。