有时,当机器学习从业者拥有的领域知识表明一个变量与另一个变量的平方、立方或其他幂相关时,从现有的某个数值特征中创建合成特征会很有用。
请考虑以下数据点分布,其中粉色圆圈代表一个类或类别(例如某种树),绿色三角形代表另一个类(或树种):
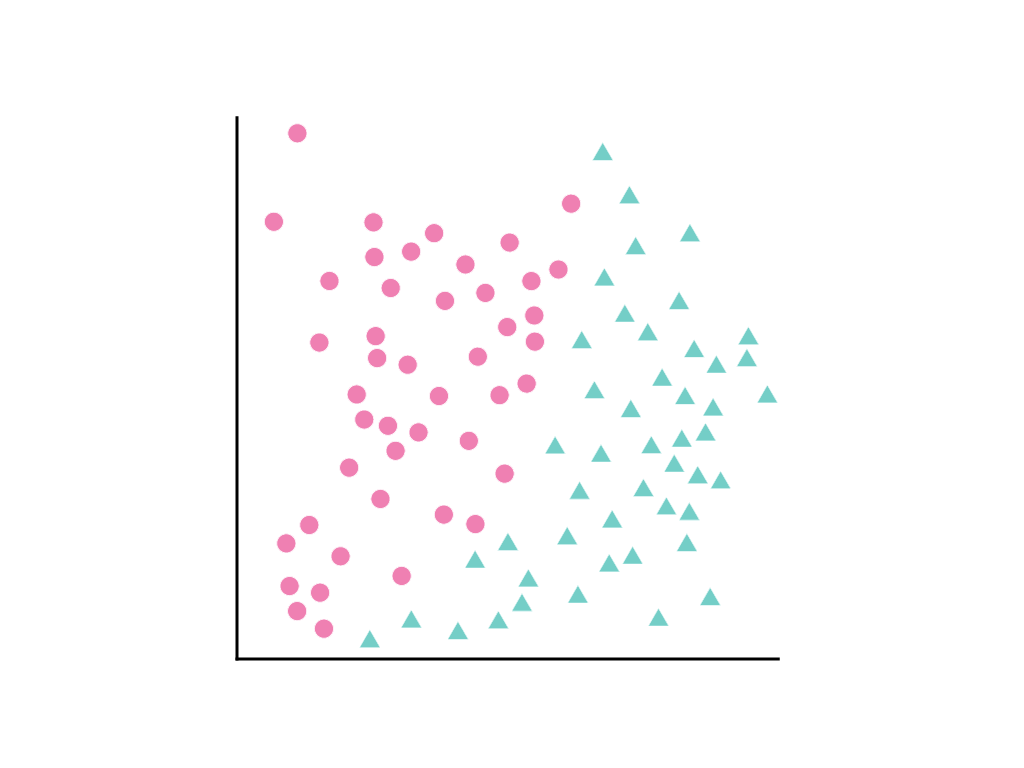
我们无法绘制一条能清晰区分这两个类的直线,但可以绘制一条能做到这一点的曲线:
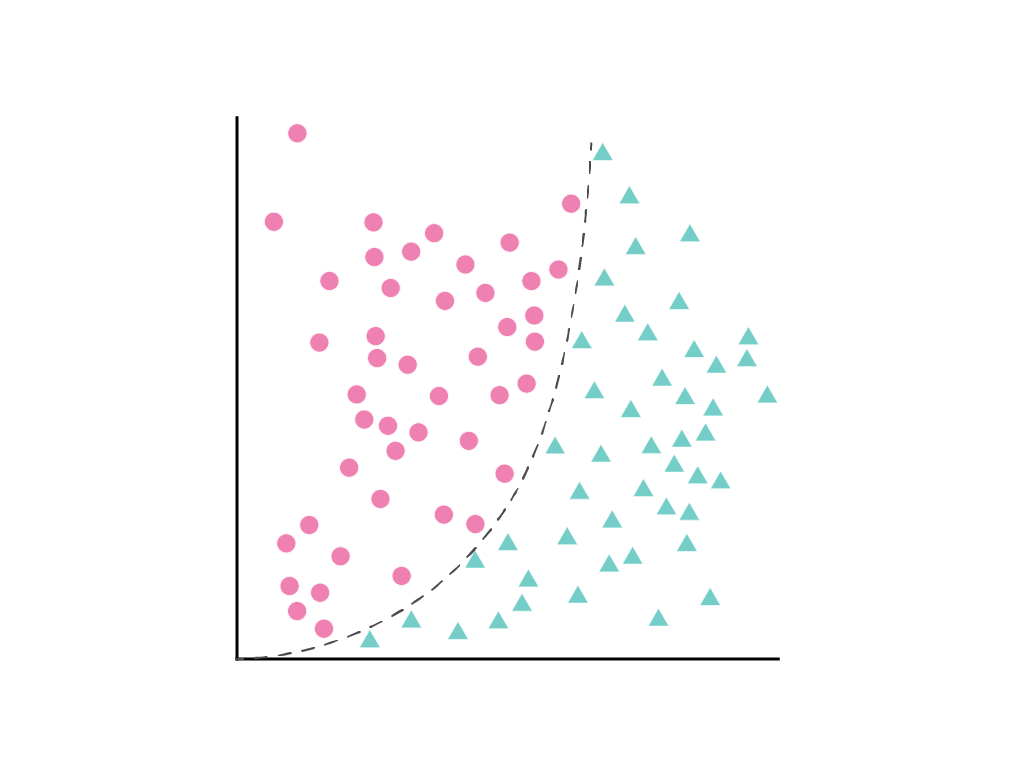
如线性回归模块中所述,具有一个特征 $x_1$ 的线性模型由线性方程描述:
通过添加术语 \(w_2x_2\)、\(w_3x_3\)等来处理其他功能。
梯度下降法会找到可最大限度地减少模型损失的权重 $w_1$(如果有其他特征,则为权重\(w_1\)、 \(w_2\)、 \(w_3\))。但显示的数据点不能用线条分隔。该怎么办?
通过定义一个新术语 \(x_2\)(即 \(x_1\) 的平方)来同时保留线性方程和允许非线性:
此合成特征(称为多项式转换)会像任何其他特征一样处理。之前的线性公式变为:
尽管包含隐藏的平方项(多项式转换),但这仍然可以视为线性回归问题,并且权重可以像往常一样通过梯度下降确定。添加多项式转换后,无需更改线性模型的训练方式,模型便可使用形式为 $y = b + w_1x + w_2x^2$ 的曲线来分隔数据点。
通常,我们会将感兴趣的数值特征乘以自身,即将其升到某个幂。有时,机器学习从业者可以根据经验对适当的指数做出合理的猜测。例如,物理世界中的许多关系都与平方项相关,包括重力加速度、光或声音随距离衰减以及弹性势能。
如果您以会更改其尺度的形式转换地图项,则应考虑尝试对其进行归一化处理。在转换后进行标准化可能会使模型的效果更好。如需了解详情,请参阅数值数据:标准化。