בקטע הזה נבחן את שלוש השאלות הבאות:
- מה ההבדל בין מערכי נתונים מאוזנים לפי מחלקות לבין מערכי נתונים לא מאוזנים לפי מחלקות?
- למה קשה לאמן מערך נתונים לא מאוזן?
- איך אפשר להתגבר על הבעיות שקשורות לאימון של מערכי נתונים לא מאוזנים?
מערכי נתונים מאוזנים לעומת מערכי נתונים לא מאוזנים
נניח שיש מערך נתונים שמכיל תווית קטגורית שהערך שלה הוא או הסיווג החיובי או הסיווג השלילי. במערך נתונים מאוזן לפי מחלקות, מספר המחלקות החיוביות ומספר המחלקות השליליות כמעט זהה. לדוגמה, קבוצת נתונים שמכילה 235 מחלקות חיוביות ו-247 מחלקות שליליות היא קבוצת נתונים מאוזנת.
במערך נתונים עם חוסר איזון בין מחלקות, תווית אחת נפוצה הרבה יותר מהאחרת. בעולם האמיתי, מערכי נתונים עם חוסר איזון בין המחלקות נפוצים הרבה יותר ממערכי נתונים עם איזון בין המחלקות. לדוגמה, במערך נתונים של עסקאות בכרטיסי אשראי, יכול להיות שרכישות הונאה יהוו פחות מ-0.1% מהדוגמאות. באופן דומה, במערך נתונים של אבחון רפואי, מספר המטופלים עם וירוס נדיר עשוי להיות פחות מ-0.01% מכלל הדוגמאות. במערך נתונים עם חוסר איזון בין הכיתות:
- התווית הנפוצה יותר more נקראת מחלקת הרוב.
- התווית פחות נפוצה נקראת מחלקת המיעוט.
הקושי באימון מערכי נתונים עם חוסר איזון חמור בין המחלקות
האימון נועד ליצור מודל שמבחין בהצלחה בין המחלקה החיובית לבין המחלקה השלילית. כדי לעשות את זה, קבוצות צריכות לכלול מספיק גם סיווגים חיוביים וגם סיווגים שליליים. זה לא מהווה בעיה כשמבצעים אימון על מערך נתונים עם חוסר איזון קל בין הסיווגים, כי בדרך כלל אפילו קבוצות קטנות מכילות מספיק דוגמאות של הסיווג החיובי והסיווג השלילי. עם זאת, יכול להיות שקבוצת נתונים עם חוסר איזון חמור בין המחלקות לא תכיל מספיק דוגמאות של המחלקה המיעוטית לאימון תקין.
לדוגמה, נתבונן במערך נתונים לא מאוזן של מחלקות שמוצג באיור 6, שבו:
- 200 תוויות נמצאות בכיתה הרוב.
- 2 תוויות שייכות לקבוצת המיעוט.
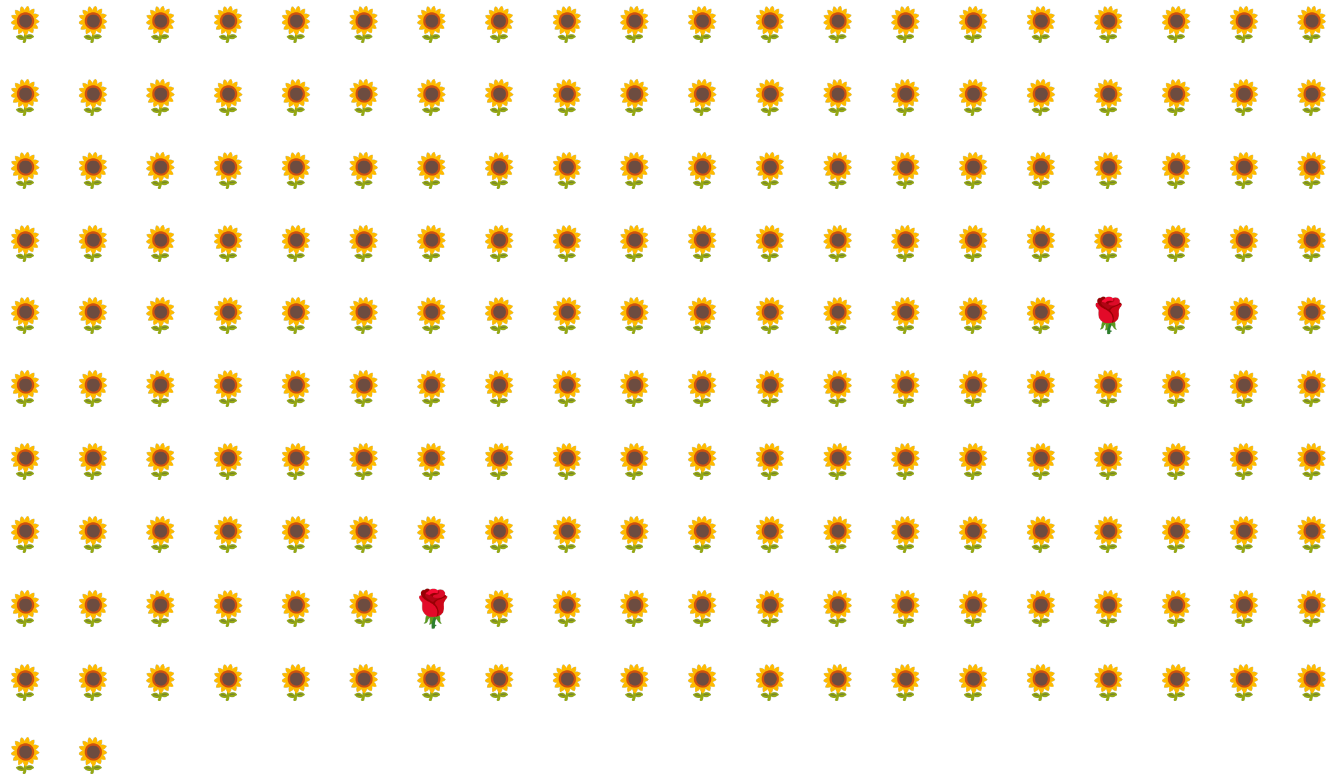
אם גודל האצווה הוא 20, רוב האצוות לא יכילו דוגמאות של מחלקת המיעוט. אם גודל האצווה הוא 100, כל אצווה תכיל בממוצע רק דוגמה אחת של מחלקה מיעוטית, וזה לא מספיק לאימון תקין. גם אם גודל האצווה יהיה גדול בהרבה, עדיין יתקבל יחס לא מאוזן כזה, והמודל לא יתאמן בצורה תקינה.
אימון מערך נתונים עם חוסר איזון בין הכיתות
במהלך האימון, המודל צריך ללמוד שני דברים:
- איך נראית כל כיתה, כלומר, אילו ערכי תכונות מתאימים לאיזו כיתה?
- כמה נפוצה כל מחלקה, כלומר מה ההתפלגות היחסית של המחלקות?
באימון רגיל, שני היעדים האלה מתערבבים. לעומת זאת, בטכניקה הבאה בת שני השלבים שנקראת דילול ומתן משקל גבוה יותר למחלקה הגדולה, שני היעדים האלה מופרדים, וכך המודל יכול להשיג את שני היעדים.
שלב 1: דגימת יתר של המחלקה העיקרית
Downsampling פירושו אימון על אחוז נמוך באופן לא פרופורציונלי של דוגמאות של מחלקת הרוב. כלומר, אתם מכריחים באופן מלאכותי מערך נתונים עם חוסר איזון בין המחלקות להיות מאוזן יותר, על ידי השמטה של הרבה דוגמאות מהמחלקה הגדולה יותר מאימון. הקטנת קצב הדגימה מגדילה מאוד את הסיכוי שכל אצווה תכיל מספיק דוגמאות של המחלקה המיעוטית כדי לאמן את המודל בצורה נכונה ויעילה.
לדוגמה, מערך הנתונים עם חוסר איזון בין הסיווגים שמוצג באיור 6 מורכב מ-99% דוגמאות של סיווג הרוב ו-1% דוגמאות של סיווג המיעוט. הקטנת מספר הדגימות של רוב המחלקות בפקטור של 25 יוצרת באופן מלאכותי מערך אימון מאוזן יותר (80% רוב המחלקות לעומת 20% מיעוט המחלקות), כפי שמוצג באיור 7:

שלב 2: הגדלת המשקל של הכיתה שנדגמה
הקטנת הדגימה יוצרת הטיה בתחזית כי היא מציגה למודל עולם מלאכותי שבו יש איזון רב יותר בין הסיווגים מאשר בעולם האמיתי. כדי לתקן את ההטיה הזו, צריך להגדיל את המשקל של רוב הסיווגים בפקטור של הדגימה שביצעתם. הגדלת המשקל פירושה התייחסות חמורה יותר להפסד בדוגמה של מחלקה גדולה יותר מאשר להפסד בדוגמה של מחלקה קטנה יותר.
לדוגמה, אם דגמנו את המחלקה הגדולה יותר בדגימת חסר (downsampling) בפקטור של 25, אנחנו צריכים להגדיל את המשקל של המחלקה הגדולה יותר בפקטור של 25. כלומר, אם המודל מנבא בטעות את המחלקה הגדולה ביותר, המערכת מתייחסת להפסד כאילו היו 25 שגיאות (מכפילה את ההפסד הרגיל ב-25).

כמה דגימות צריך להקטין וכמה משקל צריך להוסיף כדי לאזן מחדש את מערך הנתונים? כדי לקבוע את התשובה, כדאי להתנסות עם גורמים שונים של דגימה מצומצמת והגדלת משקל, בדיוק כמו שמתנסים עם היפרפרמטרים אחרים.
היתרונות של הטכניקה הזו
היתרונות של דגימת יתר והגדלת המשקל של המחלקה הגדולה:
- מודל טוב יותר: המודל שמתקבל "יודע" את שני הדברים הבאים:
- הקשר בין התכונות לבין התוויות
- ההתפלגות האמיתית של המחלקות
- התכנסות מהירה יותר: במהלך האימון, המודל רואה את מחלקת המיעוט בתדירות גבוהה יותר, מה שעוזר למודל להתכנס מהר יותר.
