Verilerinizi istatistiksel ve görselleştirme teknikleriyle inceledikten sonra verilerinizi, modelinizin eğitilmesine yardımcı olacak şekilde dönüştürmelisiniz. çeşitliliğini dikkate almıyor. Amacı normalleştirme, benzer bir ölçekte olmasını sağlıyor. Örneğin, aşağıdaki iki özelliği ele alalım:
Xözelliği 154 ile 24.917.482 arasındadır.Yözelliği, 5 ila 22 aralığını kapsar.
Bu iki özellik çok farklı aralıkları kapsar. Normalleştirme sizi etkileyebilir
X ve Y, böylece benzer bir aralığı (belki 0 ile 1 arasında) kapsarlar.
Normalleştirme şu faydaları sağlar:
- Eğitim sırasında modellerin daha hızlı yakınlaşmasına yardımcı olur. Farklı özelliklerin farklı aralıkları olduğunda, gradyan iniş "geri dönen" daha yavaş yakınlaşma anlamına gelir. Bununla birlikte, Adagrad ve Adam gibi daha gelişmiş optimizatörler, etkili öğrenme hızını zaman içinde değiştirerek bu soruna karşı koruma sağlar.
- Modellerin daha iyi tahminler elde etmesine yardımcı olur. Farklı özelliklerin farklı aralıkları olduğunda, bu, biraz daha az yararlı tahminlerde bulunabilir.
- Özellik değerleri çok yüksek olduğunda "NaN tuzağından" kaçınmanıza yardımcı olur.
NaN, not a number (sayı değil) ifadesinin kısaltmasıdır. Bir modeldeki değer, kayan nokta hassasiyet sınırını aştığında sistem, değeri bir sayı yerine
NaNolarak ayarlar. Modeldeki bir sayı NaN olduğunda, model de sonunda NaN'ye dönüşür. - Modelin her özellik için uygun ağırlıkları öğrenmesine yardımcı olur. Özellik ölçeklendirmesi olmadan model, geniş aralıklara sahip özelliklere çok fazla, dar aralıklara sahip özelliklere ise yeterince dikkat etmez.
Sayısal özellikleri, farklı alanları kapsayacak şekilde normalleştirmenizi öneririz.
farklı aralıklar (örneğin, yaş ve gelir) olabilir.
Ayrıca, geniş bir aralığı kapsayan tek bir sayısal özelliği (ör. city population.) normalleştirmenizi öneririz.
Aşağıdaki iki özelliği göz önünde bulundurun:
Aözelliğinin en düşük değeri -0,5, en yüksek değeri +0,5'tir.Bözelliğinin en düşük değeri -5,0, en yüksek değeri ise +5,0'tır.
A ve B özellikleri nispeten dar aralıklara sahiptir. Ancak, B adlı özelliğin
aralığı, A Özelliğinin süresinden 10 kat daha geniştir. Bu nedenle:
- Eğitimin başında model,
AÖzelliğinin on kat daha fazla olduğunu varsayar daha "önemli" ÖzelliktenBdaha fazla. - Eğitim olması gerekenden daha uzun sürer.
- Elde edilen model yetersiz olabilir.
Normalleştirme yapılmamasından kaynaklanan genel hasar nispeten küçük olsa da A ve B özelliklerini aynı ölçeğe (ör. -1,0 ila +1,0) normalleştirmenizi öneririz.
Şimdi, aralıklar arasında daha fazla uyumsuzluk olan iki özelliği düşünün:
Cözelliğinin en düşük değeri -1, en yüksek değeri +1'dir.Dözelliğinin en düşük değeri +5000, en yüksek değeri +1.000.000.000'dur.
C ve D özelliğini normalleştirmezseniz modeliniz
olabileceğini unutmayın. Ayrıca eğitim, süreç boyunca
birbirinden tamamen uzaklaşmak zorunda kalabilirsiniz.
Bu bölümde, üç popüler normalleştirme yöntemi ele alınmaktadır:
- doğrusal ölçeklendirme
- Z puanını ölçeklendirme
- günlük ölçeklendirme
Bu bölümde ayrıca kaydırma. Gerçek bir normalleştirme tekniği olmasa da kırpma, düzensiz sayısal özellikleri daha iyi modeller oluşturan aralıklara dönüştürür.
Lineer ölçeklendirme
Doğrusal ölçeklendirme (daha yaygın olarak ölçeklendirme olarak kısaltılmış), kayan nokta değerlerinin doğal aralıklarını standart bir aralığa böler (genellikle 0 ila 1 veya -1'den +1'e getirin.
Aşağıdaki koşulların tümü karşılanıyorsa doğrusal ölçeklendirme iyi bir seçimdir:
- Verilerinizin alt ve üst sınırları zamanla fazla değişmez.
- Özellik çok az sayıda aykırı değer içerir veya hiç aykırı değer içermez ve bu aykırı değerler aşırı değildir.
- Özellik, içerdiği aralıkta yaklaşık olarak eşit bir şekilde dağıtılmıştır. Yani histogram, çoğu değer için kabaca eşit çubuklar gösterir.
age adlı kullanıcının bir özellik olduğunu varsayalım. Doğrusal ölçeklendirme, iyi bir normalleştirmedir
age için teknik çünkü:
- Yaklaşık alt ve üst sınırlar 0 ile 100 arasındadır.
age, aykırı değerlerin nispeten küçük bir yüzdesini içeriyor. Nüfusun yalnızca yaklaşık %0,3'ü 100 yaşın üzerinde.- Belirli yaş grupları diğerlerinden biraz daha iyi temsil edilse de büyük bir veri kümesi tüm yaş gruplarına ait yeterli sayıda örnek içermelidir.
Alıştırma: Anladığınızdan emin olun
Modelinizde, ağda bulunannet_worth adlı bir özelliğin
değer katarlar. Doğrusal ölçeklendirme iyi bir normalleştirme olur mu
net_worth? Neden evet veya neden hayır?
Z puanını ölçeklendirme
Z puanı, bir değerin ortalamadan sapma sayısını ifade eder. Örneğin, ortalamadan 2 standart sapma daha büyük bir değerin Z puanı +2,0'dır. Şundan küçük 1,5 standart sapma olan bir değer: ortalamanın Z puanı -1,5'tir.
Bir özelliği Z-puanı ölçeklendirme ile temsil etmek, o özelliğin Özellik vektörindeki Z puanı. Örneğin, aşağıdaki şekilde iki histogram gösterilmektedir:
- Sol tarafta klasik bir normal dağılım gösterilmektedir.
- Sağda, aynı dağılım Z puanı ölçeklendirmesiyle normalleştirilmiştir.
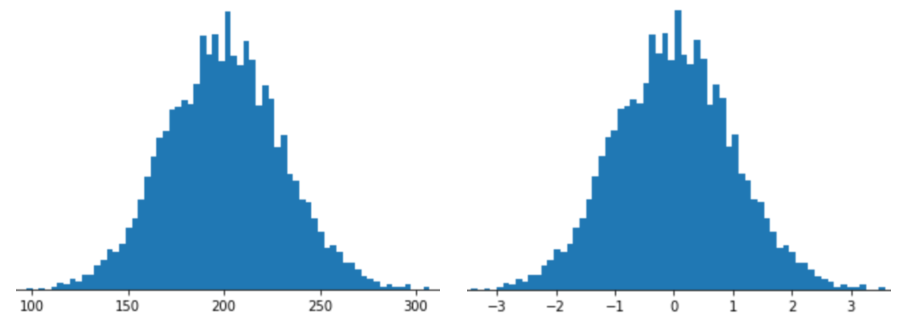
Z-puanı ölçeklendirmesi de bu tür veriler için iyi bir seçimdir. , son derece normal bir dağılıma sahiptir.
Veriler normal dağılım veya normal dağılıma benzer bir dağılım izliyorsa z-skoru iyi bir seçimdir.
Bazı dağılımların, aralıklarının büyük kısmında normal olsa bile aşırı aykırı değerler içerebileceğini unutmayın. Örneğin, geleneksel projelerin neredeyse
bir net_worth özelliğindeki puanlar 3 standart sapmaya sorunsuz bir şekilde sığabilir,
ancak bu özelliğe verilebilecek birkaç örnek, yüzlerce standart sapma
yardımcı olur. Bu gibi durumlarda, Z puanı ölçeklendirmesini başka bir normalleştirme biçimiyle (genellikle kırpma) birleştirerek bu durumu çözebilirsiniz.
Alıştırma: Anladığınızdan emin olun
Modelinizin, on milyon yetişkin kadının boylarını içerenheight adlı bir özellik üzerinde eğitildiğini varsayalım. Z puanı ölçeklendirmesi, height için iyi bir normalleştirme tekniği mi? Neden evet veya neden hayır?
Günlük ölçeklendirme
Günlük ölçeklendirme, ham değerin logaritmasını hesaplar. Teoride, logaritma herhangi bir taban olabilir; pratikte, günlük ölçeklendirmesi genellikle doğal logaritma (ln).
Veriler kuvvet yasası dağılımına uygun olduğunda günlük ölçeklendirme faydalıdır. Basitçe ifade etmek gerekirse güç yasası dağılımı aşağıdaki gibi görünür:
- Düşük
Xdeğerleri,Ygibi çok yüksek değerlere sahip. Xdeğerleri arttıkçaYdeğerleri hızla azalır. Sonuç olarak,Xyüksek değerleriYçok düşük olur.
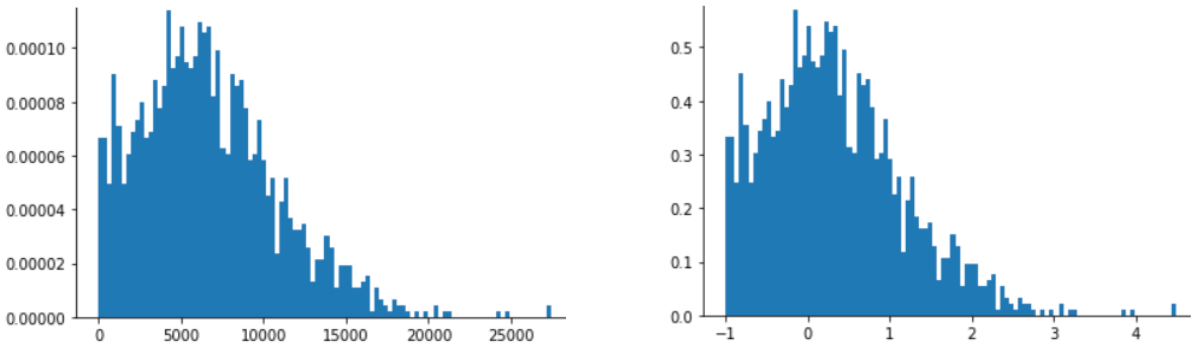
Film derecelendirmeleri, güç yasası dağılımına iyi bir örnektir. Sonraki şekil, bildirim:
- Bazı filmler çok sayıda kullanıcı oyu alır. (
X'ün düşük değerleriY'un yüksek değerlerine sahiptir.) - Çoğu filme verilen kullanıcı derecelendirmesi çok azdır. (
Xiçin yüksek değerler, düşük değerlere)Y.)
Log ölçeklendirme, dağılımı değiştirir. Bu da daha iyi tahminler yapacak bir modelin eğitilmesine yardımcı olur.

İkinci örnek olarak kitap satışları, güç yasası dağılımına uygundur çünkü:
- Yayınlanan çoğu kitabın çok az sayıda kopyası satılır. Bu sayı belki bir veya iki yüzdür.
- Bazı kitaplar binlerce olmak üzere orta sayıda kopya satar.
- Yalnızca birkaç çok satan kitap bir milyondan fazla satabilir.
İlişkiyi bulmak için doğrusal bir modeli eğittiğinizi Örneğin, kitap kapakları gibi. Ham değerler üzerine eğitilen bir doğrusal model milyonlarca satış yapan kitapların kapaklarıyla ilgili bir şeyler bulmak zorundayız. bu da yalnızca 100 kopya satan kitap kapaklarından 10.000 daha güçlüdür. Ancak tüm satış rakamlarını logaritmik ölçeklendirmek, görevi çok daha uygulanabilir hale getirir. Örneğin, 100 sayısının logaritması:
~4.6 = ln(100)
1.000.000 sayısının logaritması ise:
~13.8 = ln(1,000,000)
Yani 1.000.000'un günlüğü, 100'ün logaritmasından yalnızca üç kat daha büyüktür. En çok satan bir kitabın kapağının, az satan bir kitabın kapağına kıyasla (bir açıdan) yaklaşık üç kat daha güçlü olabileceğini tahmin edebilirsiniz.
Kırpma
Kırpma, bir teknikle Aşırılıkların etkisini en aza indirmenize yardımcı olabilir. Özetlemek gerekirse, kırpma genellikle aykırı değerlerin değerini belirli bir maksimum değerle sınırlandırır (azaltır). Kırpma, tuhaf bir fikir olsa da çok etkili olabilir.
Örneğin, çeşitli evlerdeki oda sayısını (toplam oda sayısı, ev sakinlerinin sayısına bölünür) temsil eden roomsPerPerson adlı bir özellik içeren bir veri kümesi düşünün. Aşağıdaki grafik, özellik değerlerinin %99'unun normal dağılıma (yaklaşık 1,8 ortalama ve 0,7 standart sapma) uygun olduğunu gösterir. Ancak bu özellikte, bazıları aşırı olan birkaç aykırı değer bulunur:
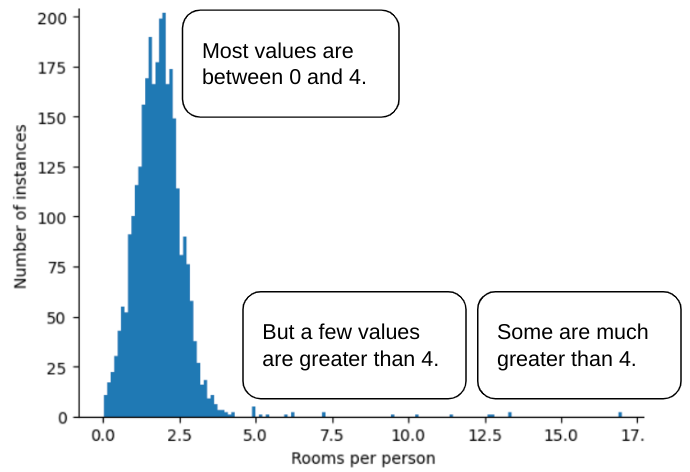
Bu uç değerlerin etkisini nasıl en aza indirebilirsiniz? Bu histogram eşit dağılım, normal dağılım veya kuvvet yasası dağılımı değildir. Maksimum değeri sınırlar veya klip eklerseniz ne olur?
roomsPerPerson isteğe bağlı bir değerde mi, örneğin 4,0 mı?
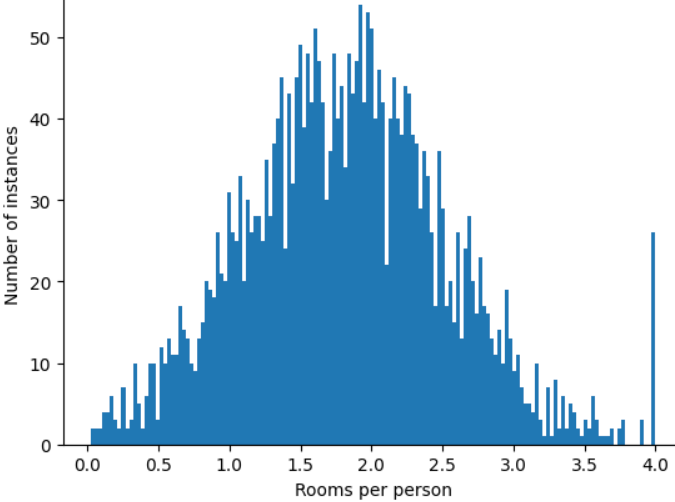
Özellik değerinin 4.0'da kırpılması, modelinizin tüm 4,0'dan büyük değerlere sahiptir. Bunun yerine, 4,0'dan büyük olan tüm değerlerin 4,0 olduğu anlamına gelir. Bu, 4,0'taki tuhaf tepeyi açıklar. Karşılığında ölçeklenmiş özellik kümesi artık orijinal verilere göre daha kullanışlı hale geliyor.
Bir saniye bekleyin. Her aykırı değer için rastgele bir üst eşiğe inebilir misiniz? Model eğitirken evet.
Değerleri, diğer normalleştirme biçimlerini uyguladıktan sonra da kırpabilirsiniz. Örneğin, Z-skoru ölçeklendirmesini kullandığınızı ancak birkaç aykırı değerin mutlak değerlerinin 3'ten çok daha büyük olduğunu varsayalım. Bu durumda şunları yapabilirsiniz:
- 3'ten büyük Z puanlarını tam 3 olacak şekilde kırpın.
- -3'ten düşük Z puanlarını tam olarak -3 olacak şekilde kırpın.
Kırpma, modelinizin önemsiz verileri fazla dizine eklemesini önler. Ancak, Bazı aykırı değerler gerçekten önemlidir; bu nedenle, klipleri dikkatli bir şekilde kırpın.
Normalleştirme tekniklerinin özeti
| Normalleştirme tekniği | Formül | Ne zaman kullanılır? |
|---|---|---|
| Lineer ölçeklendirme | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | Özellik sabit bir aralıkta eşit olarak dağıtıldığında |
| Z puanını ölçeklendirme | $$ x' = \frac{x - μ}{σ}$$ | Özellik dağılımının aşırı aykırı değerler içermediğinde. |
| Günlük ölçeklendirme | $$ x' = log(x)$$ | Özellik, güç yasasına uygun olduğunda |
| Kırpma | Eğer $x > max$, $x olarak ayarla = maks.$ Eğer $x < min$, $x olarak ayarla = dk.$ |
Özellik aşırı aykırı değerler içerdiğinde. |
Alıştırma: Bilginizi test edin

Bir veri merkezinin çalışma kabiliyetini
veri merkezi içinde ölçülen sıcaklığa göre verimlilik artışı sağlar.
Veri kümenizdeki temperature değerlerinin neredeyse tamamı 15 ile 30 (Celcius) arasındadır. Aşağıdakiler istisnadır:
- Yılda bir veya iki kez, aşırı sıcak günlerde
temperature'te 31 ile 45 arasında birkaç değer kaydedilir. temperatureiçindeki her 1.000. nokta, gerçek sıcaklık yerine 1.000 değerine ayarlanır.
Bu yaklaşım, müşteri için makul bir normalleştirme
temperature silinsin mi?
1.000 olan değerler hatalıdır ve kırpılmak yerine silinmelidir.
31 ile 45 arasındaki değerler geçerli veri noktalarıdır. Kırpma işlemi, bu değerler için iyi bir fikir olabilir; veri kümesi, bu sıcaklık aralığında yeterli sayıda örnek içermiyor doğru tahminlerde bulunacak şekilde eğitilmesidir. Ancak çıkarım sırasında, bu nedenle kırpılan modelin 35 derece, 45 derece.
