Halaman ini diterjemahkan oleh Cloud Translation API.

Data numerik: Normalisasi

Setelah memeriksa data melalui teknik statistik dan visualisasi, Anda harus mengubah data dengan cara yang akan membantu model dilatih dengan lebih efektif. Sasaran normalisasi adalah mengubah fitur agar berada pada skala yang serupa. Misalnya, pertimbangkan dua fitur berikut:

Fitur X mencakup rentang 154 hingga 24.917.482.
Fitur Y mencakup rentang 5 hingga 22.

Kedua fitur ini memiliki rentang yang sangat berbeda. Normalisasi dapat memanipulasi X dan Y sehingga mencakup rentang yang serupa, mungkin 0 hingga 1.

Normalisasi memberikan manfaat berikut:

Membantu model berkonvergensi lebih cepat selama pelatihan. Jika fitur yang berbeda memiliki rentang yang berbeda, gradien menurun dapat "memantul" dan memperlambat konvergensi. Meskipun demikian, pengoptimal yang lebih canggih seperti Adagrad dan Adam melindungi dari masalah ini dengan mengubah kecepatan belajar yang efektif dari waktu ke waktu.
Membantu model menyimpulkan prediksi yang lebih baik. Jika fitur yang berbeda memiliki rentang yang berbeda, model yang dihasilkan mungkin membuat prediksi yang kurang berguna.
Membantu menghindari "perangkap NaN" saat nilai fitur sangat tinggi. NaN adalah singkatan dari bukan angka. Jika nilai dalam model melebihi batas presisi floating point, sistem akan menetapkan nilai ke NaN, bukan angka. Saat satu angka dalam model menjadi NaN, angka lain dalam model juga pada akhirnya menjadi NaN.
Membantu model mempelajari bobot yang sesuai untuk setiap fitur. Tanpa penskalaan fitur, model akan terlalu memperhatikan fitur dengan rentang yang luas dan tidak cukup memperhatikan fitur dengan rentang sempit.

Sebaiknya normalisasi fitur numerik yang mencakup rentang yang sangat berbeda (misalnya, usia dan pendapatan). Sebaiknya normalisasi satu fitur numerik yang mencakup rentang yang luas, seperti city population.

Pertimbangkan dua fitur berikut:

Nilai terendah fitur A adalah -0,5 dan nilai tertingginya adalah +0,5.
Nilai terendah fitur B adalah -5,0 dan nilai tertingginya adalah +5,0.

Fitur A dan Fitur B memiliki rentang yang relatif sempit. Namun, span B Fitur 10 kali lebih lebar daripada span Fitur A. Jadi:

Pada awal pelatihan, model mengasumsikan bahwa Fitur B sepuluh kali lebih "penting" daripada Fitur A.
Pelatihan akan memerlukan waktu lebih lama dari yang seharusnya.
Model yang dihasilkan mungkin kurang optimal.

Kerusakan keseluruhan karena tidak melakukan normalisasi akan relatif kecil; tetapi, kami tetap merekomendasikan untuk menormalisasi Fitur A dan Fitur B ke skala yang sama, mungkin -1,0 hingga +1,0.

Sekarang, pertimbangkan dua fitur dengan perbedaan rentang yang lebih besar:

Nilai terendah fitur C adalah -1 dan nilai tertingginya adalah +1.
Nilai terendah fitur D adalah +5.000 dan nilai tertingginya adalah +1.000.000.000.

Jika Anda tidak melakukan normalisasi pada Fitur C dan Fitur D, model Anda kemungkinan akan tidak optimal. Selain itu, pelatihan akan memakan waktu lebih lama untuk dikonvergensi atau bahkan gagal dikonvergensi sepenuhnya.

Bagian ini membahas tiga metode normalisasi yang populer:

penskalaan linear
Penskalaan skor Z
penskalaan log

Bagian ini juga membahas pemangkasan. Meskipun bukan teknik normalisasi yang sebenarnya, pemotongan memang menjinakkan fitur numerik yang tidak teratur ke dalam rentang yang menghasilkan model yang lebih baik.

Skala linier

Penskalaan linear (lebih umum disingkat menjadi penskalaan) berarti mengonversi nilai floating point dari rentang alaminya menjadi rentang standar—biasanya 0 hingga 1 atau -1 hingga +1.

Klik ikon untuk melihat matematika.

Gunakan formula berikut untuk menskalakan ke rentang standar 0 hingga 1, inklusif:

$$ x' = (x - x_{min}) / (x_{max} - x_{min}) $$

dalam hal ini:

$x'$ adalah nilai yang diskalakan.
$x$ adalah nilai aslinya.
$x_{min}$ adalah nilai terendah dalam set data fitur ini.
$x_{max}$ adalah nilai tertinggi dalam set data fitur ini.

Misalnya, pertimbangkan fitur bernama quantity yang rentang alaminya berkisar antara 100 hingga 900. Misalkan nilai alami quantity dalam contoh tertentu adalah 300. Oleh karena itu, Anda dapat menghitung nilai normal 300 sebagai berikut:

$x$ = 300
$x_{min}$ = 100
$x_{maks}$ = 900

x' = (300 - 100) / (900 - 100)
x' = 200 / 800
x' = 0.25

Penskalaan linear adalah pilihan yang baik jika semua kondisi berikut terpenuhi:

Batas bawah dan atas data Anda tidak banyak berubah dari waktu ke waktu.
Fitur ini berisi sedikit atau tidak ada pencilan, dan pencilan tersebut tidak ekstrem.
Fitur ini kira-kira didistribusikan secara merata di seluruh rentangnya. Artinya, histogram akan menampilkan batang yang kira-kira sama untuk sebagian besar nilai.

Misalkan age manusia adalah fitur. Penskalaan linear adalah teknik normalisasi yang baik untuk age karena:

Perkiraan batas bawah dan atas adalah 0 hingga 100.
age berisi persentase outlier yang relatif kecil. Hanya sekitar 0,3% populasi yang berusia di atas 100 tahun.
Meskipun usia tertentu agak lebih terwakili daripada usia lainnya, set data yang besar harus berisi contoh yang memadai dari semua usia.

Latihan: Memeriksa pemahaman Anda

Misalnya, model Anda memiliki fitur bernama net_worth yang menyimpan kekayaan bersih orang yang berbeda. Apakah penskalaan linear akan menjadi teknik normalisasi yang baik untuk net_worth? Mengapa atau mengapa tidak?

Klik ikon untuk melihat jawabannya.

Jawaban: Penskalaan linear akan menjadi pilihan yang buruk untuk menormalisasi net_worth. Fitur ini berisi banyak pencilan, dan nilainya tidak didistribusikan secara seragam di seluruh rentang utamanya. Kebanyakan orang akan dijepit dalam pita yang sangat sempit dari rentang keseluruhan.

Penskalaan skor Z

Skor Z adalah jumlah simpangan baku nilai dari rata-rata. Misalnya, nilai yang 2 standar deviasi lebih besar dari nilai tengah memiliki skor Z +2,0. Nilai yang 1,5 standar deviasi lebih kecil dari rata-rata memiliki skor Z -1,5.

Merepresentasikan fitur dengan penskalaan skor Z berarti menyimpan skor Z fitur tersebut dalam vektor fitur. Misalnya, gambar berikut menunjukkan dua histogram:

Di sebelah kiri, distribusi normal klasik.
Di sebelah kanan, distribusi yang sama dinormalisasi dengan penskalaan skor Z.

Gambar 4. Dua histogram: keduanya menunjukkan distribusi normal dengan
distribusi yang identik. Histogram pertama, yang berisi data mentah, memiliki rata-rata 200 dan simpangan baku 30. Histogram kedua, yang berisi versi skor Z dari distribusi pertama, memiliki rata-rata 0 dan simpangan baku 1. — **Gambar 4.** Data mentah (kiri) versus skor Z (kanan) untuk distribusi normal.

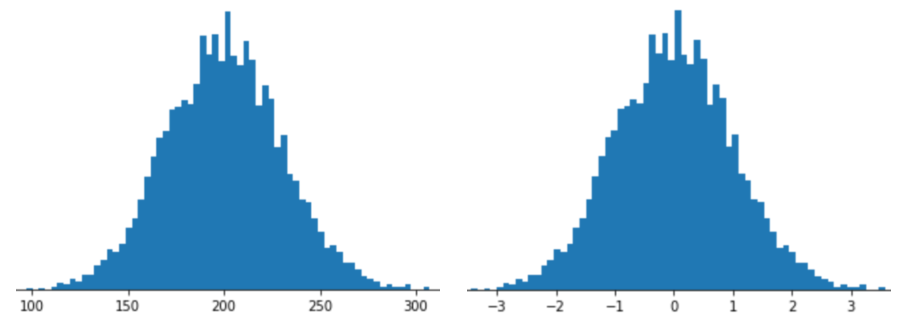
Penskalaan skor z juga merupakan pilihan yang baik untuk data seperti yang ditunjukkan dalam gambar berikut, yang hanya memiliki distribusi normal yang samar.

Gambar 5. Dua histogram bentuk identik, masing-masing menunjukkan kenaikan
curam ke dataran tinggi, lalu penurunan yang relatif cepat diikuti
pembusukan bertahap. Satu histogram mengilustrasikan
distribusi data mentah; histogram lainnya mengilustrasikan
distribusi data mentah saat dinormalisasi dengan penskalaan skor Z.
Nilai pada sumbu X dari kedua histogram sangat berbeda.
Histogram data mentah mencakup domain 0 hingga 29.000,sedangkan
histogram yang diskalakan skor Z berkisar dari -1 hingga sekitar +4, 8 — **Gambar 5.** Data mentah (kiri) versus penskalaan skor Z (kanan) untuk distribusi normal yang tidak klasik.

Klik ikon untuk melihat matematika.

Gunakan formula berikut untuk menormalisasi nilai, $x$, ke skor Z-nya:

$$ x' = (x - μ) / σ $$

dalam hal ini:

$x'$ adalah skor Z.
$x$ adalah nilai mentah; yaitu, $x$ adalah nilai yang Anda normalisasi.
$μ$ adalah nilai rata-rata.
$legal$ adalah simpangan baku.

Misalnya:

mean = 100
simpangan baku = 20
nilai asli = 130

Jadi:

  Z-score = (130 - 100) / 20
  Z-score = 30 / 20
  Z-score = +1.5

Klik ikon untuk mempelajari lebih lanjut distribusi normal.

Dalam distribusi normal klasik:

Setidaknya 68,27% data memiliki skor Z antara -1,0 dan +1,0.
Setidaknya 95,45% data memiliki skor Z antara -2,0 dan +2,0.
Setidaknya 99,73% data memiliki skor Z antara -3,0 dan +3,0.
Setidaknya 99,994% data memiliki skor Z antara -4,0 dan +4,0.

Jadi, poin data dengan skor Z kurang dari -4,0 atau lebih dari +4,0 jarang terjadi, tetapi apakah mereka benar-benar pencilan? Karena penyimpangan adalah konsep tanpa definisi yang ketat, tidak ada yang dapat memastikannya. Perhatikan bahwa set data dengan jumlah contoh yang cukup banyak pasti akan berisi setidaknya beberapa contoh "jarang" ini. Misalnya, fitur dengan satu miliar contoh yang sesuai dengan distribusi normal klasik dapat memiliki sebanyak 60.000 contoh dengan skor di luar rentang -4,0 hingga +4,0.

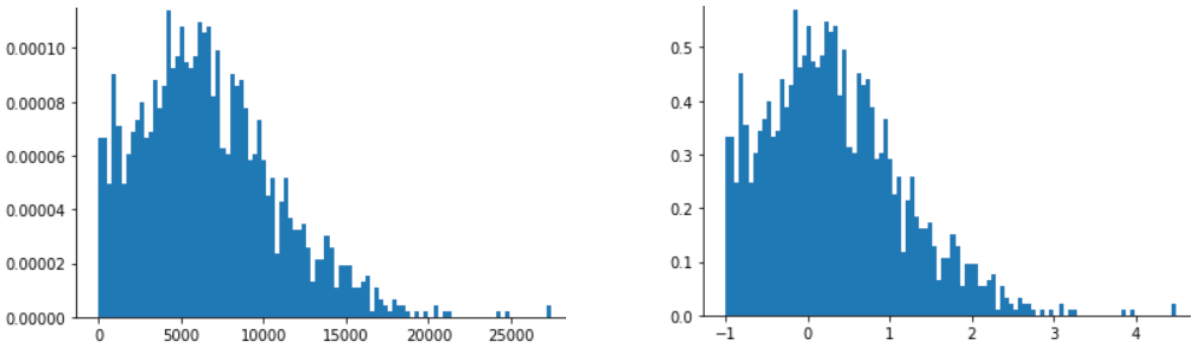
Skor Z adalah pilihan yang baik jika data mengikuti distribusi normal atau distribusi yang agak mirip dengan distribusi normal.

Perhatikan bahwa beberapa distribusi mungkin normal dalam sebagian besar rentang, tetapi masih berisi outlier ekstrem. Misalnya, hampir semua titik dalam fitur net_worth mungkin cocok dengan 3 deviasi standar, tetapi beberapa contoh fitur ini mungkin ratusan deviasi standar dari mean. Dalam situasi ini, Anda dapat menggabungkan penskalaan skor Z dengan bentuk normalisasi lain (biasanya pemangkasan) untuk menangani situasi ini.

Latihan: Periksa pemahaman Anda

Misalnya, model Anda dilatih pada fitur bernama height yang menyimpan tinggi dewasa sepuluh juta wanita. Apakah penskalaan skor Z akan menjadi teknik normalisasi yang baik untuk height? Mengapa atau mengapa tidak?

Klik ikon untuk melihat jawabannya.

Jawaban: Penskalaan skor Z akan menjadi teknik normalisasi yang baik untuk height karena fitur ini sesuai dengan distribusi normal. Sepuluh juta contoh menyiratkan banyak outlier—mungkin cukup outlier bagi model untuk mempelajari pola pada skor Z yang sangat tinggi atau sangat rendah.

Penskalaan log

Penskalaan log menghitung logaritma nilai mentah. Secara teori, logaritma dapat berupa basis apa pun; dalam praktiknya, penskalaan log biasanya menghitung logaritma natural (ln).

Klik ikon untuk melihat matematika.

Gunakan formula berikut untuk menormalisasi nilai, $x$, ke log-nya:

$$ x' = ln(x) $$

dalam hal ini:

$x'$ adalah logaritma natural dari $x$.
nilai asli = 54,598

Oleh karena itu, log nilai asli adalah sekitar 4,0:

  4.0 = ln(54.598)

Penskalaan log berguna jika data sesuai dengan distribusi hukum pangkat. Secara umum, distribusi hukum pangkat terlihat seperti berikut:

Nilai X rendah memiliki nilai Y yang sangat tinggi.
Seiring meningkatnya nilai X, nilai Y akan menurun dengan cepat. Akibatnya, nilai X yang tinggi memiliki nilai Y yang sangat rendah.

Rating film adalah contoh yang baik dari distribusi hukum pangkat. Pada gambar berikut, perhatikan:

Beberapa film memiliki banyak peringkat pengguna. (Nilai X yang rendah memiliki nilai Y yang tinggi.)
Sebagian besar film memiliki sangat sedikit rating pengguna. (Nilai X yang tinggi memiliki nilai Y yang rendah.)

Penskalaan log mengubah distribusi, yang membantu melatih model yang akan membuat prediksi yang lebih baik.

Gambar 6. Dua grafik yang membandingkan data mentah versus log data mentah.
Grafik data mentah menunjukkan banyak rating pengguna di bagian kepala, diikuti
oleh longtail. Grafik log memiliki distribusi yang lebih merata. — **Gambar 6.** Membandingkan distribusi mentah dengan log-nya.

Sebagai contoh kedua, penjualan buku sesuai dengan distribusi hukum kekuatan karena:

Sebagian besar buku yang sudah diterbitkan hanya menjual sedikit eksemplar, sekitar satu atau dua ratus.
Beberapa buku terjual dalam jumlah sedang, ribuan eksemplar.
Hanya beberapa produk terlaris yang dapat terjual lebih dari satu juta salinan.

Misalkan Anda melatih model linear untuk menemukan hubungan, misalnya sampul buku dengan penjualan buku. Pelatihan model linear pada nilai mentah harus menemukan sesuatu tentang sampul buku pada buku yang terjual sejuta eksemplar yang 10.000 kali lebih efektif daripada sampul buku yang hanya terjual 100 eksemplar. Namun, dengan melakukan penskalaan log pada semua angka penjualan, tugas ini menjadi jauh lebih mudah. Misalnya, log 100 adalah:

  ~4.6 = ln(100)

sedangkan log dari 1.000.000 adalah:

  ~13.8 = ln(1,000,000)

Jadi, log 1.000.000 hanya sekitar tiga kali lebih besar dari log 100. Anda mungkin bisa membayangkan sampul buku terlaris sekitar tiga kali lebih ampuh (dalam beberapa hal) daripada sampul buku terlaris.

Klip

Penyesuaian nilai adalah teknik untuk meminimalkan pengaruh pencilan ekstrem. Singkatnya, pemangkasan biasanya membatasi (mengurangi) nilai pencilan ke nilai maksimum tertentu. Pemangkasan adalah ide yang aneh, tetapi dapat sangat efektif.

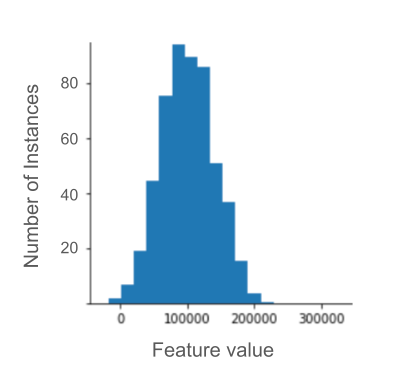
Misalnya, bayangkan set data yang berisi fitur bernama roomsPerPerson, yang mewakili jumlah kamar (total kamar dibagi dengan jumlah penghuni) untuk berbagai rumah. Plot berikut menunjukkan bahwa lebih dari 99% nilai fitur sesuai dengan distribusi normal (kira-kira, rata-rata 1,8 dan simpangan baku 0,7). Namun, fitur ini berisi beberapa pencilan, beberapa di antaranya ekstrem:

Gambar 7. Plot roomsPerPerson yang hampir semua nilainya
dikelompokkan antara 0 dan 4, tetapi ada long tail yang sangat panjang
yang mencapai hingga 17 kamar per orang — **Gambar 7.** Sebagian besar normal, tetapi tidak sepenuhnya normal.

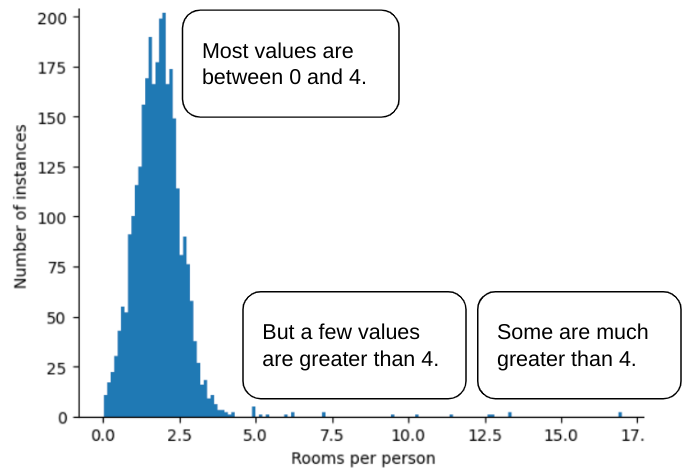
Bagaimana cara meminimalkan pengaruh pencilan ekstrem tersebut? Histogram bukanlah distribusi merata, distribusi normal, atau distribusi hukum pangkat. Bagaimana jika Anda hanya menetapkan batas atau memotong nilai maksimum roomsPerPerson pada nilai arbitrer, misalnya 4,0?

Plot roomsPerPerson dengan semua nilai antara 0 dan
4,0. Plot berbentuk lonceng, tetapi ada bukit anomali pada 4,0 — **Gambar 8.** Memotong nilai fitur pada 4.0.

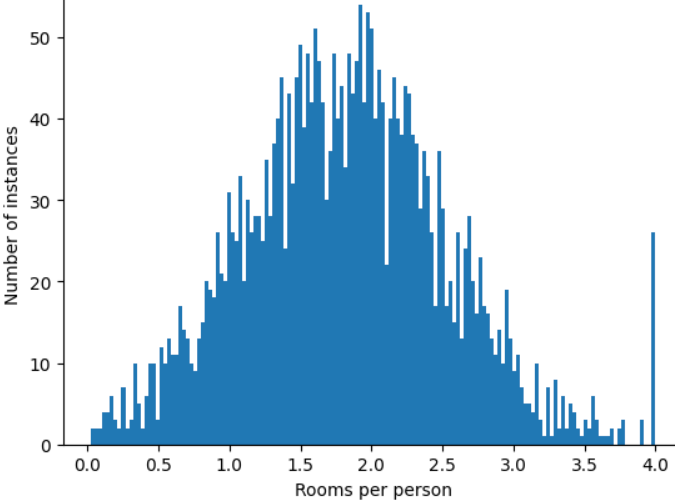
Memotong nilai fitur pada 4,0 tidak berarti model Anda mengabaikan semua nilai yang lebih besar dari 4,0. Sebaliknya, ini berarti semua nilai yang lebih besar dari 4.0 sekarang menjadi 4.0. Hal ini menjelaskan bukit aneh di 4.0. Terlepas dari bukit tersebut, set fitur yang diskalakan kini lebih berguna daripada data asli.

Tunggu sebentar! Dapatkah Anda benar-benar mengurangi setiap nilai outlier ke beberapa nilai minimum arbitrer? Saat melatih model, ya.

Anda juga dapat memangkas nilai setelah menerapkan bentuk normalisasi lainnya. Misalnya, Anda menggunakan penskalaan skor Z, tetapi beberapa pencilan memiliki nilai absolut yang jauh lebih besar dari 3. Dalam hal ini, Anda dapat:

Memotong skor Z yang lebih besar dari 3 menjadi persis 3.
Memotong skor Z kurang dari -3 menjadi persis -3.

Pemangkasan mencegah model Anda melakukan over-pengindeksan pada data yang tidak penting. Namun, beberapa pencilan sebenarnya penting, jadi pangkas nilai dengan hati-hati.

Ringkasan teknik normalisasi

Teknik normalisasi	Formula	Kapan digunakan
Skala linier	$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$	Saat fitur didistribusikan secara seragam dalam rentang tetap.
Penskalaan skor Z	$$ x' = \frac{x - μ}{σ}$$	Jika distribusi fitur tidak berisi pencilan yang ekstrem.
Penskalaan log	$$ x' = log(x)$$	Jika fitur sesuai dengan hukum kekuatan.
Pemangkasan	Jika $x > max$, tetapkan $x' = max$ Jika $x < min$, tetapkan $x' = min$	Jika fitur berisi pencilan ekstrem.

Latihan: Uji pengetahuan Anda

Teknik mana yang paling sesuai untuk menormalisasi fitur dengan distribusi berikut?

Histogram yang menampilkan cluster data dengan nilai dalam rentang 0 hingga
200.000. Jumlah titik data secara bertahap meningkat untuk rentang
dari 0 hingga 100.000, lalu secara bertahap menurun dari 100.000 menjadi
200.000.

Penskalaan skor Z

Titik data umumnya sesuai dengan distribusi normal, sehingga penskalaan skor Z akan memaksanya ke dalam rentang –3 hingga +3.

Skala linier

Tinjau diskusi tentang teknik normalisasi di halaman ini, lalu coba lagi.

Penskalaan log

Tinjau diskusi teknik normalisasi di halaman ini, dan coba lagi.

Pemangkasan

Tinjau diskusi tentang teknik normalisasi di halaman ini, lalu coba lagi.

Misalkan Anda sedang mengembangkan model yang memprediksi produktivitas pusat data berdasarkan suhu yang diukur di dalam pusat data. Hampir semua nilai temperature dalam set data Anda berada antara 15 dan 30 (Celsius), dengan pengecualian berikut:

Sekali atau dua kali per tahun, pada hari yang sangat panas, beberapa nilai antara 31 dan 45 dicatat dalam temperature.
Setiap titik ke-1.000 di temperature ditetapkan ke 1.000, bukan suhu sebenarnya.

Manakah yang akan menjadi teknik normalisasi yang wajar untuk temperature?

Pangkas nilai outlier antara 31 dan 45, tetapi hapus outlier dengan nilai 1.000

Nilai 1.000 merupakan kesalahan,dan harus dihapus, bukan terpotong.

Nilai antara 31 dan 45 adalah titik data yang sah. Clipping mungkin akan cocok untuk nilai-nilai ini, dengan asumsi set data tidak berisi cukup contoh dalam rentang suhu ini untuk melatih model agar dapat membuat prediksi yang baik. Namun, selama inferensi, perhatikan bahwa model yang terpotong akan membuat prediksi yang sama untuk suhu 45 dan suhu 35.

Buat klip semua pencilan (outliers)

Tinjau diskusi tentang teknik normalisasi di halaman ini, lalu coba lagi.

Menghapus semua pencilan

Tinjau diskusi tentang teknik normalisasi di halaman ini, lalu coba lagi.

Hapus nilai outlier antara 31 dan 45, tetapi potong outlier dengan nilai 1.000.

Tinjau diskusi tentang teknik normalisasi di halaman ini, lalu coba lagi.

Sebelumnya

Latihan pemrograman (10 mnt)

Berikutnya

Pengelompokan (15 mnt)