통계 및 시각화 기법을 통해 데이터를 검토한 후 모델이 더 효과적으로 학습할 수 있도록 데이터를 변환해야 합니다. 정규화의 목표는 변수를 비슷한 범위로 변환하는 것입니다. 예를 들어 다음 두 기능을 고려해 보세요.
- 기능
X은 154~24,917,482 범위에 걸쳐 있습니다. - 기능
Y은 5~22 범위에 걸쳐 있습니다.
이 두 기능은 매우 다른 범위를 포함합니다. 정규화는 X와 Y이 비슷한 범위(예: 0~1)에 걸쳐 있도록 조작할 수 있습니다.
정규화는 다음과 같은 이점을 제공합니다.
- 학습 중에 모델이 더 빠르게 수렴하도록 지원합니다. 특성마다 범위가 다르면 경사 하강법이 '바운스'되어 수렴이 느려질 수 있습니다. 하지만 Adagrad 및 Adam과 같은 고급 옵티마이저는 시간이 지남에 따라 효과적인 학습률을 변경하여 이 문제를 방지합니다.
- 모델이 더 나은 예측을 추론하도록 지원합니다. 서로 다른 특징의 범위가 다른 경우 결과 모델에서 유용성이 다소 떨어지는 예측을 할 수 있습니다.
- 특성 값이 매우 높은 경우 'NaN 트랩'을 방지하는 데 도움이 됩니다.
NaN은 숫자가 아님의 약어입니다. 모델의 값이 부동 소수점 정밀도 한도를 초과하면 시스템은 값을 숫자 대신
NaN으로 설정합니다. 모델의 숫자 중 하나가 NaN이 되면 모델의 다른 숫자도 결국 NaN이 됩니다. - 모델이 각 특성의 적절한 가중치를 학습하는 데 도움이 됩니다. 특성을 조정하지 않으면 모델에서 범위가 넓은 특성을 과도하게 중시하고 범위가 좁은 특성은 충분히 중시하지 않습니다.
명확하게 다른 범위를 포함하는 숫자 특성 (예: 연령 및 소득)을 정규화하는 것이 좋습니다.
또한 city population.와 같이 넓은 범위를 포함하는 단일 숫자 특성을 정규화하는 것이 좋습니다.
다음 두 가지 기능을 고려하세요.
A기능의 최솟값은 -0.5이고 최댓값은 +0.5입니다.- 기능
B의 최솟값은 -5.0이고 최댓값은 +5.0입니다.
기능 A와 기능 B의 범위는 비교적 좁습니다. 하지만 기능 B의 범위는 기능 A의 범위보다 10배 넓습니다. 따라서 날짜는 다음과 같이 계산합니다.
- 학습이 시작될 때 모델은 특성
B이 특성A보다 10배 더 '중요'하다고 가정합니다. - 학습 시간이 예상보다 오래 걸립니다.
- 결과 모델이 최적이 아닐 수 있습니다.
정규화하지 않아 발생하는 전체 손상은 비교적 작습니다. 하지만 특성 A와 특성 B를 동일한 스케일(예: -1.0~+1.0)로 정규화하는 것이 좋습니다.
이제 범위의 차이가 더 큰 두 가지 기능을 고려해 보겠습니다.
- 특성
C의 최솟값은 -1이고 최댓값은 +1입니다. D기능의 최솟값은 +5,000이고 최댓값은 +1,000,000,000입니다.
특성 C와 특성 D를 정규화하지 않으면 모델이 최적화되지 않을 수 있습니다. 또한 학습이 수렴하는 데 훨씬 더 오래 걸리거나 완전히 수렴하지 못할 수도 있습니다.
이 섹션에서는 세 가지 인기 있는 정규화 방법을 설명합니다.
- 선형 조정
- Z-점수 스케일링
- 로그 조정
이 섹션에서는 클리핑도 다룹니다. 클리핑은 실제 정규화 기법은 아니지만, 다루기 힘든 숫자 특성을 더 나은 모델을 생성하는 범위로 조정합니다.
선형 조정
선형 스케일링(일반적으로 스케일링으로 줄여서 사용)은 부동 소수점 값을 자연스러운 범위에서 표준 범위(일반적으로 0~1 또는 -1~+1)로 변환하는 것을 의미합니다.
선형 확장은 다음 조건을 모두 충족하는 경우에 적합합니다.
- 시간이 지나도 데이터의 하한과 상한이 크게 변하지 않습니다.
- 특성에 이상치가 거의 없거나 이상치가 있더라도 극단적이지 않습니다.
- 특성이 범위 전체에 대략적으로 균일하게 분포되어 있습니다. 즉, 히스토그램은 대부분의 값에 대해 거의 균등한 막대를 표시합니다.
사람 age이 특징이라고 가정해 보겠습니다. 선형 스케일링은 다음과 같은 이유로 age에 적합한 정규화 기법입니다.
- 대략적인 하한과 상한은 0~100입니다.
age에는 이상치가 상대적으로 적게 포함되어 있습니다. 인구의 약 0.3% 만이 100세를 넘습니다.- 특정 연령대가 다른 연령대보다 더 잘 표현되지만, 대규모 데이터 세트에는 모든 연령대의 예가 충분히 포함되어야 합니다.
연습: 학습 내용 점검하기
모델에 여러 사람의 순자산을 보유하는net_worth이라는 기능이 있다고 가정해 보겠습니다. 선형 스케일링이 net_worth에 적합한 정규화 기법인가요? 그 이유는 무엇인가요?
Z-점수 스케일링
Z-점수는 값이 평균에서 얼마나 떨어져 있는지 나타내는 표준 편차 수입니다. 예를 들어 평균보다 표준편차가 2만큼 큰 값의 Z 점수는 +2.0입니다. 평균보다 표준 편차가 1.5 적은 값의 Z 점수는 -1.5입니다.
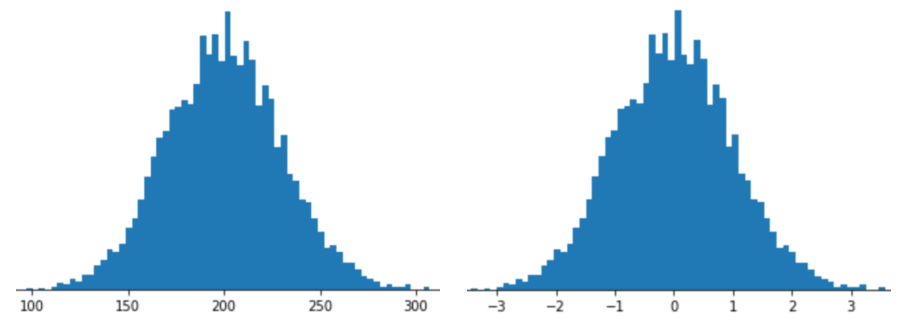
Z 점수 스케일링으로 특성을 표현한다는 것은 특성 벡터에 해당 특성의 Z 점수를 저장한다는 의미입니다. 예를 들어 다음 그림은 두 개의 히스토그램을 보여줍니다.
- 왼쪽은 일반적인 정규 분포입니다.
- 오른쪽에는 Z-점수 조정으로 정규화된 동일한 분포가 표시됩니다.
Z-점수 스케일링은 대략적인 정규 분포만 있는 다음 그림과 같은 데이터에도 적합합니다.
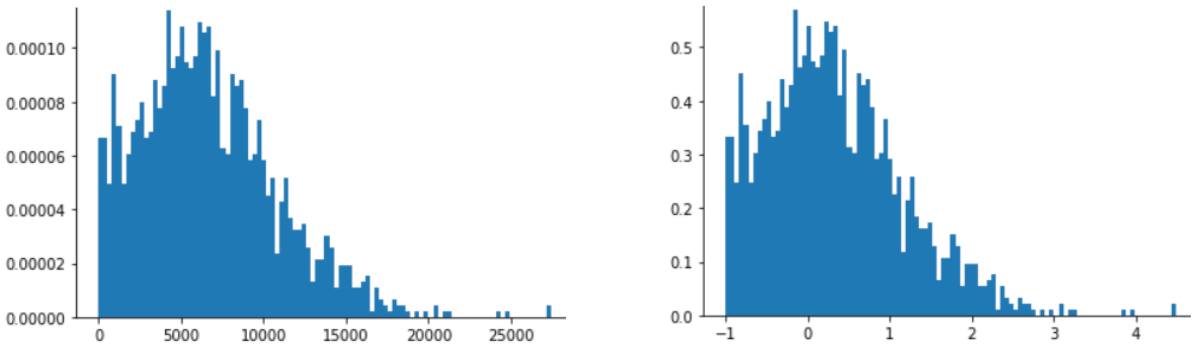
Z 점수는 데이터가 정규 분포 또는 정규 분포와 유사한 분포를 따르는 경우에 적합합니다.
일부 분포는 대부분의 범위 내에서 정상일 수 있지만 극단적인 이상치를 포함할 수도 있습니다. 예를 들어 net_worth 기능의 거의 모든 점이 표준 편차 3에 적합할 수 있지만 이 기능의 몇 가지 예는 평균에서 수백 개의 표준 편차만큼 떨어져 있을 수 있습니다. 이러한 경우 Z 점수 스케일링을 다른 형태의 정규화 (일반적으로 클리핑)와 결합하여 이 상황을 처리할 수 있습니다.
연습: 학습 내용 점검하기
모델이 성인 여성 1,000만 명의 키를 보유한height이라는 특성으로 학습한다고 가정해 보겠습니다. Z-점수 조정이 height에 적합한 정규화 기법인가요? 그 이유는 무엇인가요?
로그 조정
로그 스케일링은 원시 값의 로그를 계산합니다. 이론적으로 로그는 어떤 밑이라도 가능하지만, 실제로는 로그 스케일링이 일반적으로 자연 로그 (ln)를 계산합니다.
로그 스케일링은 데이터가 멱법칙 분포를 따를 때 유용합니다. 간단히 말해, 거듭제곱 법칙 분포는 다음과 같습니다.
X값이 낮으면Y값이 매우 높습니다.X값이 증가하면Y값이 빠르게 감소합니다. 따라서X값이 높으면Y값이 매우 낮습니다.
영화 등급은 멱법칙 분포의 좋은 예입니다. 다음 그림에서 다음 사항에 유의하세요.
- 사용자 평점이 많은 영화도 있습니다. (
X값이 낮으면Y값이 높습니다.) - 대부분의 영화에는 사용자 평점이 거의 없습니다. (
X값이 높으면Y값이 낮습니다.)
로그 스케일링은 분포를 변경하여 더 나은 예측을 하는 모델을 학습하는 데 도움이 됩니다.

두 번째 예로, 도서 판매는 다음과 같은 이유로 거듭제곱 법칙 분포를 따릅니다.
- 대부분의 출판된 책은 100~200권 정도의 적은 수로 판매됩니다.
- 일부 도서는 수천 권의 적당한 판매량을 기록합니다.
- 100만 부 이상 판매되는 베스트셀러는 몇 권에 불과합니다.
예를 들어 책 표지와 책 판매량의 관계를 파악하기 위해 선형 모델을 학습시킨다고 가정해 보겠습니다. 원시 값으로 학습하는 선형 모델은 백만 부가 판매되는 책의 책 표지가 100부만 판매되는 책의 책 표지보다 10,000배 더 강력하다는 사실을 찾아야 합니다. 하지만 모든 판매 수치를 로그 스케일링하면 훨씬 더 실현 가능해집니다. 예를 들어 100의 로그는 다음과 같습니다.
~4.6 = ln(100)
1,000,000의 로그는 다음과 같습니다.
~13.8 = ln(1,000,000)
따라서 1,000,000의 로그는 100의 로그보다 약 3배만 큽니다. 베스트셀러 도서 표지가 판매량이 적은 도서 표지보다 어떤 면에서든 3배 더 강력하다고 상상할 수 있습니다.
클리핑
경사 제한은 극단적인 이상치의 영향을 최소화하는 기법입니다. 간단히 말해, 클리핑은 일반적으로 이상치의 값을 특정 최댓값으로 제한(감소)합니다. 클리핑은 이상한 아이디어이지만 매우 효과적일 수 있습니다.
예를 들어 다양한 주택의 방 수 (총 방 수를 거주자 수로 나눈 값)를 나타내는 roomsPerPerson라는 특성이 포함된 데이터 세트를 생각해 보세요. 다음 그림은 99% 이상의 특성 값이 정규 분포 (대략 평균 1.8, 표준 편차 0.7)를 따르는 것을 보여줍니다. 하지만 이 기능에는 몇 가지 이상치가 있으며 그중 일부는 극단적입니다.
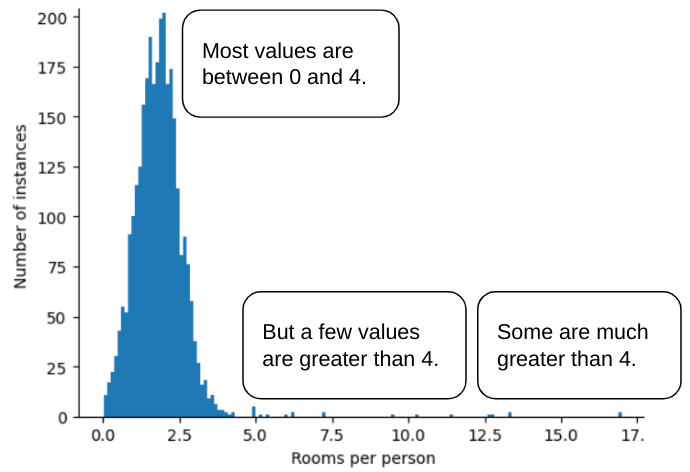
이러한 극단적인 이상치의 영향을 최소화하려면 어떻게 해야 할까요? 히스토그램이 균등 분포, 정규 분포 또는 거듭제곱 법칙 분포가 아닙니다. roomsPerPerson의 최댓값을 임의의 값(예: 4.0)으로 제한하거나 클립하면 어떻게 될까요?
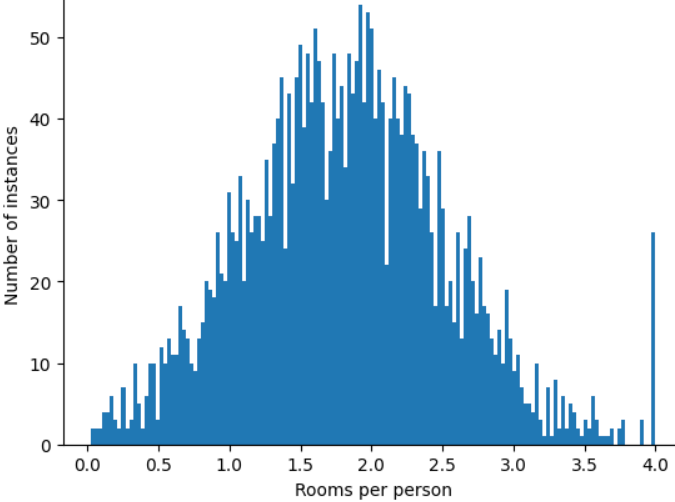
특성 값을 4.0으로 클리핑한다고 해서 모델이 4.0보다 큰 값을 모두 무시하는 것은 아닙니다. 4.0보다 큰 모든 값이 이제 4.0이 된다는 의미입니다. 이것이 4.0에 있는 특이한 언덕을 설명합니다. 이러한 문제에도 불구하고 확장된 기능 세트는 이제 원래 데이터보다 더 유용합니다.
잠시만요! 정말로 모든 이상치 값을 임의의 상한 기준점으로 줄일 수 있나요? 모델을 학습시킬 때는 가능합니다.
다른 형태의 정규화를 적용한 후 값을 클리핑할 수도 있습니다. 예를 들어 Z 점수 스케일링을 사용하지만 일부 이상치의 절대값이 3보다 훨씬 크다고 가정해 보겠습니다. 이 경우 다음을 수행할 수 있습니다.
- 3보다 큰 Z 점수를 정확히 3이 되도록 자릅니다.
- -3 미만의 Z 점수를 정확히 -3으로 자릅니다.
클리핑을 사용하면 모델이 중요하지 않은 데이터에 과도하게 인덱싱하는 것을 방지할 수 있습니다. 하지만 일부 이상치는 실제로 중요하므로 값을 신중하게 클리핑하세요.
정규화 기법 요약
| 정규화 기법 | 수식 | 사용하기 적합한 경우 |
|---|---|---|
| 선형 조정 | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | 기능이 범위에 걸쳐 대부분 균일하게 분포된 경우 납작한 모양 |
| Z-점수 스케일링 | $$ x' = \frac{x - μ}{σ}$$ | 기능이 정규 분포인 경우 (평균에 가까운 피크) 종 모양 |
| 로그 조정 | $$ x' = log(x)$$ | 특성 분포가 꼬리의 한쪽 이상으로 심하게 치우쳐 있는 경우 Heavy Tail-shaped |
| 클리핑 | $x > max$인 경우 $x' = max$로 설정 $x < min$인 경우 $x' = min$으로 설정 |
특성에 극단적인 이상치가 포함된 경우 |
연습: 지식 테스트하기

데이터 센터 내부에서 측정된 온도를 기반으로 데이터 센터의 생산성을 예측하는 모델을 개발한다고 가정해 보겠습니다.
데이터 세트의 거의 모든 temperature 값이 15~30 (섭씨) 사이에 있습니다. 다음은 예외입니다.
- 매우 더운 날에는 연간 한두 번
temperature에 31~45 사이의 값이 기록됩니다. temperature의 1,000번째 포인트는 실제 온도 대신 1,000으로 설정됩니다.
temperature에 적합한 정규화 기법은 무엇인가요?
1,000 값은 실수이며 클리핑하는 대신 삭제해야 합니다.
31~45 사이의 값은 적법한 데이터 포인트입니다. 데이터 세트에 모델이 양질의 예측을 하도록 학습하기에 충분한 이 온도 범위의 예가 포함되어 있지 않다고 가정하면 이러한 값에 클리핑을 적용하는 것이 좋습니다. 하지만 추론 중에 클리핑된 모델은 35도의 온도와 45도의 온도에 대해 동일한 예측을 합니다.