אחרי שבודקים את הנתונים באמצעות טכניקות סטטיסטיות וויזואליות, צריך לבצע טרנספורמציה של הנתונים בדרכים שיעזרו לאמן את המודל בצורה יעילה יותר. המטרה של נורמליזציה היא להפוך את התכונות כך שיהיו בסקאלה דומה. לדוגמה, נניח שיש לכם את שתי התכונות הבאות:
- התכונה
Xמשתרעת על הטווח 154 עד 24,917,482. - התכונה
Yמשתרעת על הטווח 5 עד 22.
הטווחים של שני המאפיינים האלה שונים מאוד. יכול להיות שהנורמליזציה תשנה את X ואת Y כך שהן יתפרסו על פני טווח דומה, אולי 0 עד 1.
היתרונות של נורמליזציה:
- עוזרת למודלים להתכנס מהר יותר במהלך האימון. אם למאפיינים שונים יש טווחים שונים, יכול להיות שהירידה בשיפוע תהיה לא יציבה ותאט את ההתכנסות. עם זאת, אלגוריתמים מתקדמים יותר לאופטימיזציה, כמו Adagrad ו-Adam, מונעים את הבעיה הזו על ידי שינוי קצב הלמידה האפקטיבי לאורך זמן.
- עוזרת למודלים להסיק תחזיות טובות יותר. אם לתכונות שונות יש טווחים שונים, יכול להיות שהמודל שיתקבל יפיק תחזיות פחות שימושיות.
- עוזרת להימנע מבעיית NaN כשערכי המאפיינים גבוהים מאוד.
NaN הוא קיצור של not a number (לא מספר). אם ערך במודל חורג ממגבלת הדיוק של נקודה צפה, המערכת מגדירה את הערך ל-
NaNבמקום למספר. כשמספר אחד במודל הופך ל-NaN, גם מספרים אחרים במודל הופכים בסופו של דבר ל-NaN. - המאפיין הזה עוזר למודל ללמוד משקלים מתאימים לכל תכונה. בלי שינוי קנה מידה של התכונות, המודל מקדיש יותר מדי תשומת לב לתכונות עם טווחים רחבים ולא מספיק תשומת לב לתכונות עם טווחים צרים.
מומלץ לבצע נרמול של תכונות מספריות שמכסות טווחים שונים באופן מובהק (לדוגמה, גיל והכנסה).
מומלץ גם לבצע נרמול של מאפיין מספרי יחיד שמכסה טווח רחב, כמו city population.
כדאי להביא בחשבון את שתי התכונות הבאות:
- הערך הנמוך ביותר של התכונה
Aהוא -0.5 והערך הגבוה ביותר הוא +0.5. - הערך הנמוך ביותר של התכונה
Bהוא -5.0 והערך הגבוה ביותר הוא +5.0.
הטווחים של התכונה A והתכונה B צרים יחסית. עם זאת, טווח התאריכים של תכונה B גדול פי 10 מטווח התאריכים של תכונה A. לכן:
- בתחילת האימון, המודל מניח שהתכונה
Bחשובה פי עשרה יותר מהתכונהA. - תהליך האימון יימשך יותר זמן מהרגיל.
- יכול להיות שהמודל שיתקבל לא יהיה אופטימלי.
הנזק הכולל כתוצאה מאי-נרמול יהיה קטן יחסית, אבל אנחנו עדיין ממליצים לנרמל את תכונה א' ואת תכונה ב' לאותו קנה מידה, למשל מ-1.0- עד 1.0+.
עכשיו נבחן שני פיצ'רים עם טווחים שונים בהרבה:
- הערך הנמוך ביותר של המאפיין
Cהוא -1 והערך הגבוה ביותר הוא +1. - הערך הנמוך ביותר של המאפיין
Dהוא +5,000 והערך הגבוה ביותר הוא +1,000,000,000.
אם לא תבצעו נרמול של מאפיין C ומאפיין D, סביר להניח שהמודל לא יהיה אופטימלי. בנוסף, יידרש הרבה יותר זמן כדי שהאימון יתכנס, או שהוא אפילו לא יתכנס בכלל.
בקטע הזה נסביר על שלוש שיטות נפוצות לנרמול:
- שינוי קנה מידה לינארי
- שינוי גורף של ציון תקן
- שינוי גורף בבידינג
בנוסף, בקטע הזה מוסבר על חיתוך. למרות שזו לא טכניקה אמיתית של נרמול, חיתוך עוזר להפוך מאפיינים מספריים לא מסודרים לטווחים שמניבים מודלים טובים יותר.
קנה מידה לינארי
קנה מידה לינארי (בדרך כלל מקצרים את המונח לקנה מידה) פירושו המרה של ערכים עשרוניים מהטווח הטבעי שלהם לטווח סטנדרטי – בדרך כלל 0 עד 1 או -1 עד +1.
התאמה לינארית היא בחירה טובה כשמתקיימים כל התנאים הבאים:
- הגבולות התחתון והעליון של הנתונים לא משתנים הרבה לאורך זמן.
- התכונה מכילה מעט חריגים או לא מכילה חריגים בכלל, והחריגים האלה לא קיצוניים.
- התכונה מתפלגת באופן אחיד בערך בטווח שלה. כלומר, בהיסטוגרמה יוצגו עמודות שוות בערך לרוב הערכים.
נניח שage הוא תכונה. קנה מידה ליניארי הוא שיטת נורמליזציה טובה ל-age כי:
- הגבולות התחתון והעליון המשוערים הם 0 עד 100.
ageמכיל אחוז קטן יחסית של ערכים חריגים. רק כ-0.3% מהאוכלוסייה הם בני יותר מ-100.- למרות שגילים מסוימים מיוצגים בצורה טובה יותר מאחרים, מערך נתונים גדול צריך להכיל מספיק דוגמאות של כל הגילים.
תרגיל: בדיקת ההבנה
נניח שלמודל שלכם יש תכונה בשםnet_worth שמכילה את השווי הנקי של אנשים שונים. האם קנה מידה לינארי הוא טכניקת נירמול טובה ל-net_worth? למה או למה לא?
שינוי גורף של ציון תקן
ציון Z הוא מספר סטיות התקן שערך מסוים רחוק מהממוצע. לדוגמה, ערך שהוא 2 סטיות תקן גדולות מהממוצע, מקבל ציון Z של +2.0. ערך שהוא 1.5 סטיות תקן מתחת לממוצע מקבל ציון Z של -1.5.
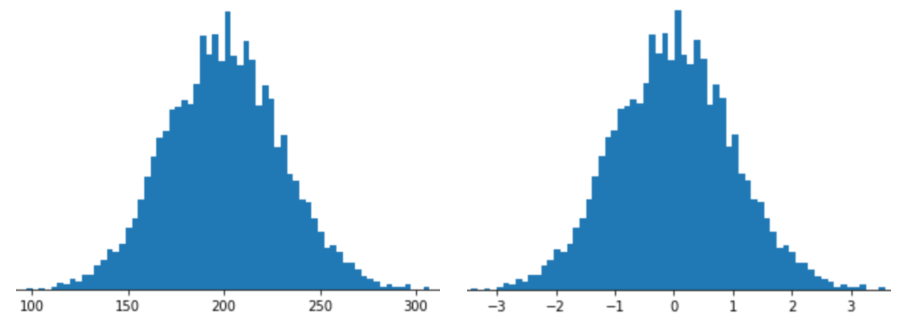
ייצוג תכונה באמצעות קנה מידה של Z-score פירושו אחסון של ה-Z-score של התכונה בווקטור התכונות. לדוגמה, באיור הבא מוצגים שני היסטוגרמות:
- מימין, התפלגות נורמלית קלאסית.
- משמאל, אותה התפלגות מנורמלת על ידי קנה מידה של ציון Z.
התאמת קנה מידה של ציון Z היא גם בחירה טובה לנתונים כמו אלה שמוצגים באיור הבא, שיש להם רק התפלגות נורמלית מעורפלת.
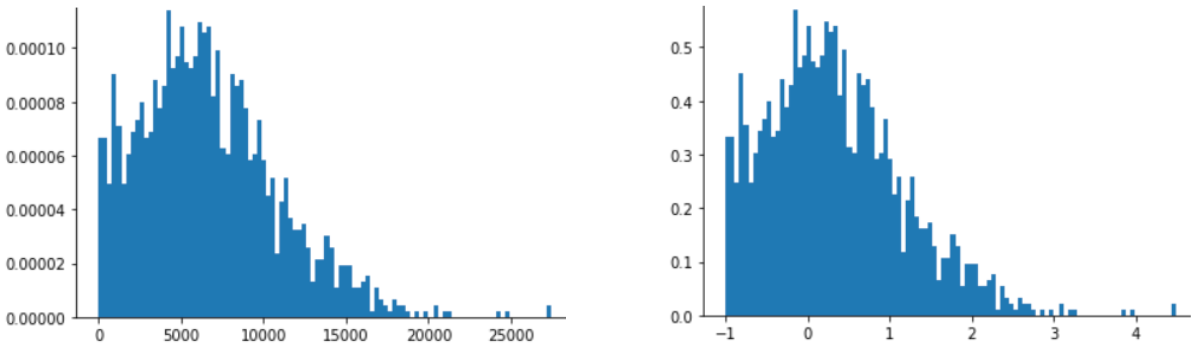
ציון Z הוא בחירה טובה כשהנתונים מתפלגים באופן נורמלי או באופן שדומה להתפלגות נורמלית.
חשוב לדעת: יכול להיות שחלק מההתפלגויות יהיו נורמליות ברוב הטווח שלהן, אבל עדיין יכללו ערכים חריגים קיצוניים. לדוגמה, כמעט כל הנקודות בתכונה net_worth עשויות להתאים בצורה מסודרת ל-3 סטיות תקן, אבל כמה דוגמאות של התכונה הזו יכולות להיות במרחק של מאות סטיות תקן מהממוצע. במקרים כאלה, אפשר לשלב בין שינוי קנה מידה של ציון Z לבין סוג אחר של נורמליזציה (בדרך כלל חיתוך) כדי לטפל במצב הזה.
תרגיל: בדיקת ההבנה
נניח שהמודל מתאמן על תכונה בשםheight שמכילה את הגבהים של עשרה מיליון נשים בבגרות. האם שינוי קנה מידה של ציון תקן יהיה טכניקת נרמול טובה ל-height? למה או למה לא?
שינוי גודל היומן
בסולם לוגריתמי, המערכת מחשבת את הלוגריתם של הערך הגולמי. באופן תיאורטי, הלוגריתם יכול להיות בכל בסיס. בפועל, בדרך כלל משתמשים בסקאלת לוגריתם כדי לחשב את הלוגריתם הטבעי (ln).
שינוי קנה מידה ללוגריתמי מועיל כשהנתונים תואמים להתפלגות חוק החזקה. במילים פשוטות, התפלגות חוק החזקה נראית כך:
- ערכים נמוכים של
Xמתאימים לערכים גבוהים מאוד שלY. - ככל שהערכים של
Xעולים, הערכים שלYיורדים במהירות. לכן, ערכים גבוהים שלXמתאימים לערכים נמוכים מאוד שלY.
סיווגי סרטים הם דוגמה טובה להתפלגות חוק חזקה. באיור הבא אפשר לראות:
- יש כמה סרטים עם הרבה דירוגים של משתמשים. (ערכים נמוכים של
Xמייצגים ערכים גבוהים שלY). - לרוב הסרטים יש מעט מאוד דירוגים של משתמשים. (ערכים גבוהים של
Xהם ערכים נמוכים שלY).
שינוי קנה המידה של היומן משנה את ההתפלגות, ועוזר לאמן מודל שיספק תחזיות טובות יותר.

דוגמה נוספת: מכירות של ספרים מתאימות להתפלגות חוק החזקה כי:
- רוב הספרים שמתפרסמים מוכרים מספר קטן מאוד של עותקים, אולי מאה או מאתיים.
- חלק מהספרים נמכרים במספר מתון של עותקים, באלפים.
- רק כמה ספרים רבי-מכר ימכרו יותר ממיליון עותקים.
נניח שאתם מאמנים מודל לינארי כדי למצוא את הקשר בין, למשל, כריכות של ספרים לבין מכירות של ספרים. מודל לינארי שאומן על ערכים גולמיים יצטרך למצוא משהו לגבי כריכות של ספרים שנמכרים במיליון עותקים, שהוא בעל השפעה חזקה פי 10,000 מכריכות של ספרים שנמכרים ב-100 עותקים בלבד. אבל אם משתמשים בסקאלה לוגריתמית כדי להציג את כל נתוני המכירות, המשימה הופכת להרבה יותר פשוטה. לדוגמה, הלוגריתם של 100 הוא:
~4.6 = ln(100)
בעוד שהלוג של 1,000,000 הוא:
~13.8 = ln(1,000,000)
לכן, הלוג של 1,000,000 גדול פי שלושה בערך מהלוג של 100. סביר להניח שאפשר לדמיין שכריכה של ספר רב-מכר חזקה פי שלושה (במובן מסוים) מכריכה של ספר שנמכר בכמויות קטנות.
חיתוך
חיתוך הוא טכניקה לצמצום ההשפעה של חריגים קיצוניים. בקיצור, חיתוך בדרך כלל מגביל (מפחית) את הערך של חריגים לערך מקסימלי ספציפי. הגזירה היא רעיון מוזר, אבל היא יכולה להיות יעילה מאוד.
לדוגמה, נניח שיש מערך נתונים שמכיל מאפיין בשם roomsPerPerson, שמייצג את מספר החדרים (מספר החדרים הכולל חלקי מספר הדיירים) בבתים שונים. מהתרשים הבא אפשר לראות שיותר מ-99% מערכי המאפיינים תואמים להתפלגות נורמלית (בערך, ממוצע של 1.8 וסטיית תקן של 0.7). עם זאת, התכונה מכילה כמה חריגים, חלקם קיצוניים:
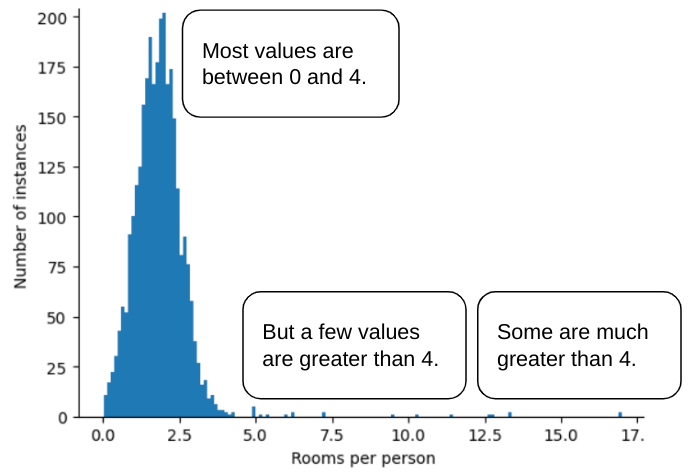
איך אפשר לצמצם את ההשפעה של החריגים הקיצוניים האלה? ובכן, ההיסטוגרמה לא מייצגת התפלגות אחידה, התפלגות נורמלית או התפלגות חוק חזקה. מה קורה אם פשוט מגבילים או מצמצמים את הערך המקסימלי של roomsPerPerson לערך שרירותי, למשל 4.0?
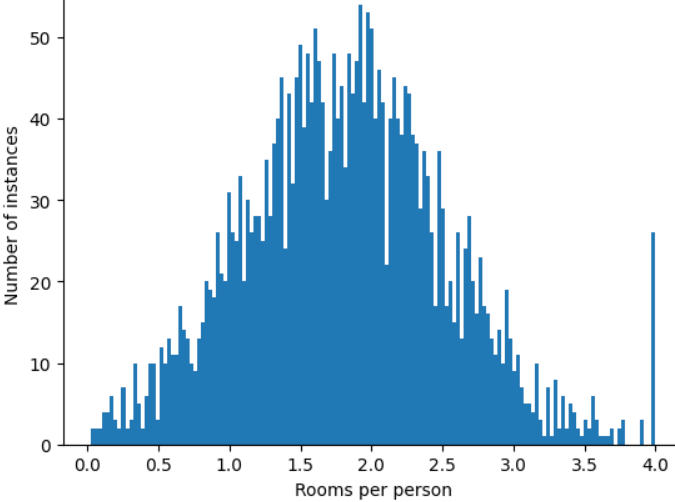
חיתוך ערך התכונה ב-4.0 לא אומר שהמודל מתעלם מכל הערכים שגדולים מ-4.0. המשמעות היא שכל הערכים שהיו גדולים מ-4.0 יהפכו עכשיו ל-4.0. זה מסביר את העלייה המוזרה בנקודה 4.0. למרות הקושי הזה, קבוצת התכונות המותאמת שימושית יותר מהנתונים המקוריים.
רגע! האם באמת אפשר לצמצם כל ערך חריג לסף עליון שרירותי כלשהו? כן, כשמאמנים מודל.
אפשר גם לחתוך ערכים אחרי שמחילים צורות אחרות של נורמליזציה. לדוגמה, נניח שאתם משתמשים בסקאלת Z, אבל לכמה ערכים חריגים יש ערכים מוחלטים שגדולים בהרבה מ-3. במקרה כזה, תוכלו:
- ערכי Z-score שגדולים מ-3 נחתכים ל-3.
- ערכי Z-score של קליפים שקטנים מ-3- יהפכו ל-3-.
הגזירה מונעת מהמודל להתמקד יותר מדי בנתונים לא חשובים. עם זאת, חלק מהערכים החריגים חשובים, לכן צריך לחתוך את הערכים בזהירות.
סיכום של טכניקות נורמליזציה
| טכניקת נורמליזציה | נוסחה | מתי להשתמש? |
|---|---|---|
| קנה מידה לינארי | $$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ | כשהתכונה מפוזרת באופן אחיד ברוב הטווח. שטוח |
| שינוי גורף של ציון תקן | $$ x' = \frac{x - μ}{σ}$$ | כשהתכונה מתפלגת נורמלית (השיא קרוב לממוצע). בצורת פעמון |
| שינוי גודל היומן | $$ x' = log(x)$$ | כשהפיזור של התכונה מוטה מאוד לפחות לאחד מהצדדים של הזנב. Heavy Tail-shaped |
| חיתוך | אם $x > max$, $x' = max$ אם $x < min$, $x' = min$ |
כשהתכונה מכילה ערכים חריגים קיצוניים. |
תרגיל: בחינת הידע

נניח שאתם מפתחים מודל שמנבא את הפרודוקטיביות של מרכז נתונים על סמך הטמפרטורה שנמדדת בתוך מרכז הנתונים.
כמעט כל הערכים של temperature במערך הנתונים הם בין 15 ל-30 (במעלות צלזיוס), עם החריגים הבאים:
- פעם או פעמיים בשנה, בימים חמים במיוחד, נרשמים כמה ערכים בין 31 ל-45 ב-
temperature. - כל נקודה אלפית ב-
temperatureמוגדרת כ-1,000 במקום הטמפרטורה בפועל.
מהי טכניקת נרמול סבירה עבור temperature?
הערכים 1,000 הם טעויות, וצריך למחוק אותם ולא לחתוך אותם.
הערכים בין 31 ל-45 הם נקודות נתונים לגיטימיות. כדאי להגביל את הערכים האלה, בהנחה שאין מספיק דוגמאות בטווח הטמפרטורות הזה במערך הנתונים כדי לאמן את המודל ליצירת תחזיות טובות. עם זאת, במהלך ההיקש, שימו לב שהמודל עם הערכים המוגבלים ייתן את אותה תחזית לטמפרטורה של 45 כמו לטמפרטורה של 35.