Числовые данные: нормализация

После изучения ваших данных с помощью методов статистики и визуализации вам следует преобразовать их таким образом, чтобы ваша модель могла обучаться более эффективно. Цель нормализации — преобразовать объекты в одинаковый масштаб. Например, рассмотрим следующие две особенности:

• Функция X охватывает диапазон от 154 до 24 917 482.
• Функция Y охватывает диапазон от 5 до 22.

Эти две функции охватывают очень разные диапазоны. Нормализация может манипулировать X и Y так, чтобы они охватывали одинаковый диапазон, например, от 0 до 1.

Нормализация дает следующие преимущества:

• Помогает моделям быстрее сходиться во время обучения. Когда разные функции имеют разные диапазоны, градиентный спуск может «отскакивать» и замедлять сходимость. Тем не менее, более продвинутые оптимизаторы, такие как Adagrad и Adam, защищают от этой проблемы, изменяя эффективную скорость обучения с течением времени.
• Помогает моделям делать более точные прогнозы . Когда разные функции имеют разные диапазоны, результирующая модель может давать несколько менее полезные прогнозы.
• Помогает избежать «ловушки NaN», когда значения функции очень высоки. NaN — это сокращение, а не число . Когда значение в модели превышает предел точности с плавающей запятой, система устанавливает значение NaN вместо числа. Когда одно число в модели становится NaN, другие числа в модели также в конечном итоге становятся NaN.
• Помогает модели узнать соответствующие веса для каждой функции. Без масштабирования функций модель уделяет слишком много внимания функциям с широкими диапазонами и недостаточно внимания функциям с узкими диапазонами.

Мы рекомендуем нормализовать числовые характеристики, охватывающие совершенно разные диапазоны (например, возраст и доход). Мы также рекомендуем нормализовать один числовой признак, охватывающий широкий диапазон, например city population.

Предупреждение. Если вы нормализуете функцию во время обучения, вы также должны нормализовать эту функцию при составлении прогнозов.

Учитывайте следующие две особенности:

• Наименьшее значение функции A составляет -0,5, а максимальное — +0,5.
• Наименьшее значение функции B составляет -5,0, а максимальное — +5,0.

Функция A и функция B имеют относительно узкие диапазоны. Однако диапазон функции B в 10 раз шире, чем диапазон функции A Поэтому:

• В начале обучения модель предполагает, что Feature A в десять раз более «важна», чем Feature B
• Обучение займет больше времени, чем следовало бы.
• Полученная модель может оказаться неоптимальной.

Общий ущерб из-за отсутствия нормализации будет относительно небольшим; однако мы по-прежнему рекомендуем нормализовать функцию A и функцию B к одному и тому же масштабу, например, от -1,0 до +1,0.

Теперь рассмотрим две особенности с большим несоответствием диапазонов:

• Наименьшее значение функции C равно -1, а максимальное – +1.
• Наименьшее значение признака D составляет +5000, а максимальное — [phone].

Если вы не нормализуете Feature C и Feature D , ваша модель, скорее всего, будет неоптимальной. Более того, обучение займет гораздо больше времени, чтобы сблизиться или даже не сойдется полностью!

В этом разделе рассматриваются три популярных метода нормализации:

• линейное масштабирование
• Масштабирование Z-оценки
• масштабирование журнала

В этом разделе дополнительно рассматривается обрезка . Хотя отсечение и не является настоящим методом нормализации, оно укрощает неуправляемые числовые характеристики и превращает их в диапазоны, позволяющие создавать более качественные модели.

Линейное масштабирование

Линейное масштабирование (чаще сокращается до простого масштабирования ) означает преобразование значений с плавающей запятой из их естественного диапазона в стандартный диапазон — обычно от 0 до 1 или от -1 до +1.

Нажмите на значок, чтобы увидеть математические вычисления.

Используйте следующую формулу для масштабирования до стандартного диапазона от 0 до 1 включительно:

$$ x' = (x - x_{min}) / (x_{max} - x_{min}) $$

где:

• $x'$ — масштабированное значение.
• $x$ — исходное значение.
• $x_{min}$ — это наименьшее значение в наборе данных этого объекта.
• $x_{max}$ — это наибольшее значение в наборе данных этого объекта.

Например, рассмотрим объект с именем quantity , естественный диапазон которого составляет от 100 до 900. Предположим, что натуральное значение quantity в конкретном примере равно 300. Следовательно, вы можете вычислить нормализованное значение 300 следующим образом:

• $х$ = 300
• $x_{мин}$ = 100
• $x_{макс}$ = 900

x' = (300 - 100) / (900 - 100)
x' = 200 / 800
x' = 0.25

---

Линейное масштабирование является хорошим выбором, если соблюдены все следующие условия:

• Нижняя и верхняя границы ваших данных не сильно меняются со временем.
• Объект содержит мало выбросов или вообще не содержит выбросов, и эти выбросы не являются экстремальными.
• Объект примерно равномерно распределен по всему диапазону. То есть гистограмма будет отображать примерно одинаковые столбцы для большинства возрастов.

Предположим, age человека является особенностью. Линейное масштабирование является хорошим методом нормализации age , потому что:

• Приблизительные нижняя и верхняя границы составляют от 0 до 100.
• age содержит относительно небольшой процент выбросов. Лишь около 0,3% населения старше 100 лет.
• Хотя некоторые возрасты представлены несколько лучше, чем другие, большой набор данных должен содержать достаточное количество примеров всех возрастов.

Примечание. Большинство реальных функций не соответствуют всем критериям линейного масштабирования. Масштабирование Z-показателя обычно является лучшим выбором для нормализации, чем линейное масштабирование.

Упражнение: Проверьте свое понимание.

Предположим, в вашей модели есть функция с именем net_worth , которая хранит чистую стоимость разных людей. Будет ли линейное масштабирование хорошим методом нормализации для net_worth ? Почему или почему нет?

Нажмите на значок, чтобы увидеть ответ.

Ответ: Линейное масштабирование будет плохим выбором для нормализации net_worth . Этот объект содержит множество выбросов, и значения неравномерно распределены по его основному диапазону. Большинство людей оказались бы зажаты в очень узкую полосу общего диапазона.

---

Масштабирование Z-оценки

Z-показатель — это количество стандартных отклонений значения от среднего значения. Например, значение, которое на 2 стандартных отклонения превышает среднее значение, имеет Z-показатель +2,0. Значение, которое на 1,5 стандартных отклонения меньше среднего, имеет Z-показатель -1,5.

Представление объекта с масштабированием Z-показателя означает сохранение Z-показателя этого объекта в векторе признаков. Например, на следующем рисунке показаны две гистограммы:

• Слева — классическое нормальное распределение.
• Справа то же распределение, нормализованное с помощью масштабирования Z-показателя.

Рисунок 4. Необработанные данные (слева) и Z-показатель (справа) для нормального распределения.

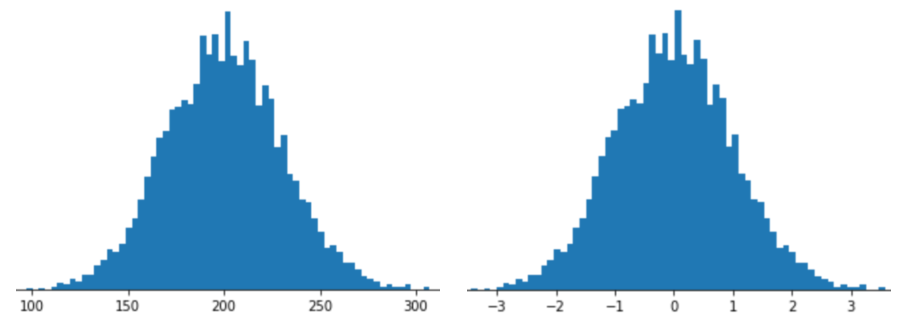
Масштабирование Z-показателя также является хорошим выбором для данных, подобных показанным на следующем рисунке, которые имеют лишь приблизительно нормальное распределение.

Рисунок 5. Необработанные данные (слева) и масштабирование Z-показателя (справа) для неклассического нормального распределения.

Нажмите на значок, чтобы увидеть математические вычисления.

Используйте следующую формулу, чтобы нормализовать значение $x$ к его Z-показателю:

$$ x' = (x - μ) / σ $$

где:

• $x'$ — это Z-оценка.
• $x$ — необработанное значение; то есть $x$ — это значение, которое вы нормализуете.
• $μ$ — среднее значение.
• $σ$ — стандартное отклонение.

Например, предположим:

• среднее = 100
• стандартное отклонение = 20
• исходное значение = 130

Поэтому:

  Z-score = (130 - 100) / 20
  Z-score = 30 / 20
  Z-score = +1.5

---

Щелкните значок, чтобы узнать больше о нормальных распределениях.

В классическом нормальном распределении:

• По крайней мере, 68,27% данных имеют Z-показатель от -1,0 до +1,0.
• По крайней мере, 95,45% данных имеют Z-показатель от -2,0 до +2,0.
• По крайней мере, 99,73% данных имеют Z-показатель от -3,0 до +3,0.
• По крайней мере, 99,994% данных имеют Z-показатель от -4,0 до +4,0.

Итак, точки данных с Z-показателем менее -4,0 или более +4,0 встречаются редко, но являются ли они действительно выбросами? Поскольку выбросы — это понятие, не имеющее строгого определения, никто не может сказать наверняка. Обратите внимание, что набор данных с достаточно большим количеством примеров почти наверняка будет содержать хотя бы несколько таких «редких» примеров. Например, объект с одним миллиардом примеров, соответствующий классическому нормальному распределению, может иметь до 60 000 примеров с оценкой вне диапазона от -4,0 до +4,0.

---

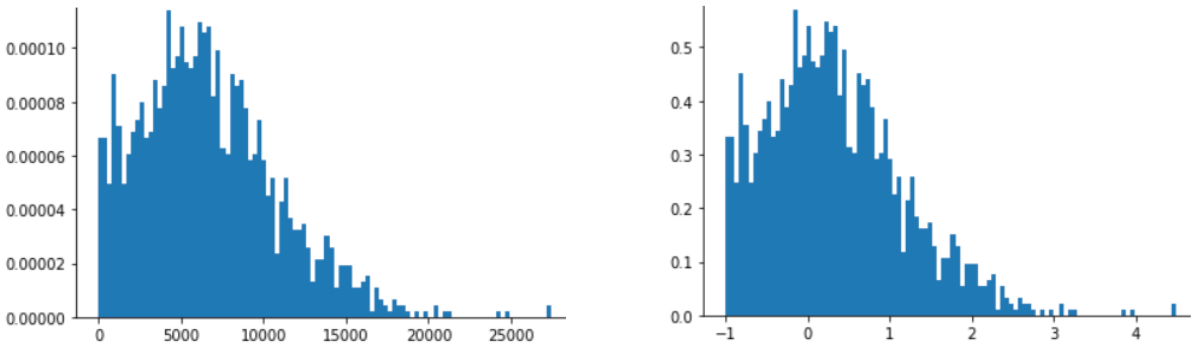
Z-показатель является хорошим выбором, когда данные подчиняются нормальному распределению или распределению, напоминающему нормальное распределение.

Обратите внимание, что некоторые распределения могут быть нормальными в большей части своего диапазона, но все же содержать крайние выбросы. Например, почти все точки функции net_worth могут аккуратно укладываться в 3 стандартных отклонения, но некоторые примеры этой функции могут отклоняться от среднего значения на сотни стандартных отклонений. В таких ситуациях вы можете комбинировать масштабирование Z-показателя с другой формой нормализации (обычно обрезкой), чтобы справиться с этой ситуацией.

Упражнение: Проверьте свое понимание.

Предположим, ваша модель тренируется на признаке « height , который содержит рост десяти миллионов женщин. Будет ли масштабирование Z-показателя хорошим методом нормализации height ? Почему или почему нет?

Нажмите на значок, чтобы увидеть ответ.

Ответ: Масштабирование Z-показателя было бы хорошим методом нормализации height , поскольку этот признак соответствует нормальному распределению. Десять миллионов примеров подразумевают большое количество выбросов — вероятно, достаточное количество выбросов, чтобы модель могла изучить закономерности при очень высоких или очень низких значениях Z.

---

Масштабирование журнала

Логарифмическое масштабирование вычисляет логарифм необработанного значения. Теоретически логарифм может быть любым основанием; на практике при логарифмическом масштабировании обычно вычисляется натуральный логарифм (ln).

Нажмите на значок, чтобы увидеть математические вычисления.

Используйте следующую формулу, чтобы нормализовать значение $x$ к его журналу:

$$ x' = ln(x) $$

где:

• $x'$ — натуральный логарифм числа $x$.
• исходное значение = 54,598

Следовательно, логарифм исходного значения составляет около 4,0:

  4.0 = ln(54.598)

---

Логарифмическое масштабирование полезно, когда данные соответствуют степенному закону распределения. Упрощенно степенное распределение выглядит следующим образом:

• Низкие значения X имеют очень высокие значения Y
• По мере увеличения значений X значения Y быстро уменьшаются. Следовательно, высокие значения X имеют очень низкие значения Y

Рейтинги фильмов являются хорошим примером степенного закона распределения. На следующем рисунке обратите внимание:

• Некоторые фильмы имеют множество пользовательских оценок. (Низкие значения X соответствуют высоким значениям Y )
• Большинство фильмов имеют очень мало пользовательских оценок. (Высокие значения X имеют низкие значения Y )

Масштабирование журнала изменяет распределение, что помогает обучить модель, которая будет давать более точные прогнозы.

Рисунок 6. Сравнение необработанного дистрибутива с его журналом.

Второй пример: продажи книг подчиняются степенному закону распределения, потому что:

• Большинство опубликованных книг продаются небольшим тиражом, может быть, одна или двести.
• Некоторые книги продаются умеренным тиражом, исчисляемым тысячами.
• Лишь немногие бестселлеры будут проданы тиражом более миллиона копий.

Предположим, вы обучаете линейную модель, чтобы найти связь, скажем, между обложками книг и продажами книг. Обучение линейной модели на необработанных значениях должно было бы найти что-то об обложках книг, которые продаются миллионным тиражом, что на 10 000 мощнее, чем обложки книг, которые продаются всего 100 экземпляров. Однако логарифмическое масштабирование всех показателей продаж делает задачу гораздо более осуществимой. Например, журнал 100:

  ~4.6 = ln(100)

в то время как журнал 1 000 000:

  ~13.8 = ln(1,000,000)

Таким образом, журнал 1 000 000 всего лишь примерно в три раза больше, чем журнал 100. Вы, вероятно, можете себе представить, что обложка бестселлера примерно в три раза более мощная (в некотором смысле), чем обложка книги, продаваемой крошечными тиражами.

Обрезка

Отсечение — это метод минимизации влияния экстремальных выбросов. Короче говоря, обрезка обычно ограничивает (уменьшает) значение выбросов до определенного максимального значения. Отсечение — странная идея, но тем не менее она может быть очень эффективной.

Например, представьте себе набор данных, содержащий объект с roomsPerPerson , который представляет количество комнат (общее количество комнат, разделенное на количество жильцов) в различных домах. Следующий график показывает, что более 99% значений признаков соответствуют нормальному распределению (примерно среднее значение 1,8 и стандартное отклонение 0,7). Однако эта функция содержит несколько отклонений, некоторые из них экстремальные:

Рисунок 7. В основном нормально, но не совсем нормально.

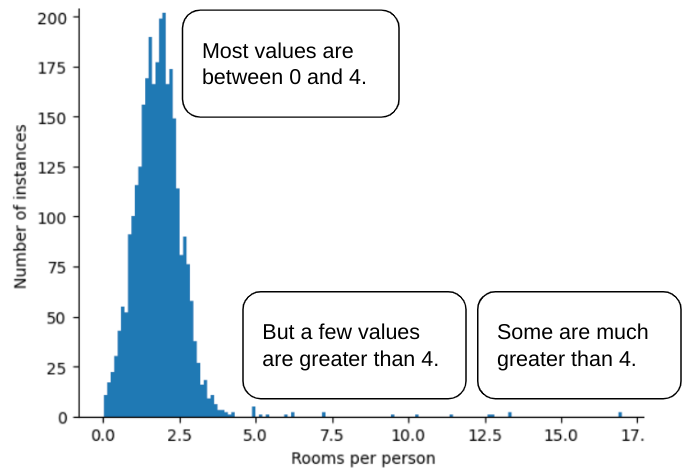
Как можно минимизировать влияние этих крайних выбросов? Что ж, гистограмма не является ровным, нормальным или степенным распределением. Что, если вы просто ограничите или обрежете максимальное roomsPerPerson произвольным значением, скажем, 4,0?

Рисунок 8. Значения функций отсечения в версии 4.0.

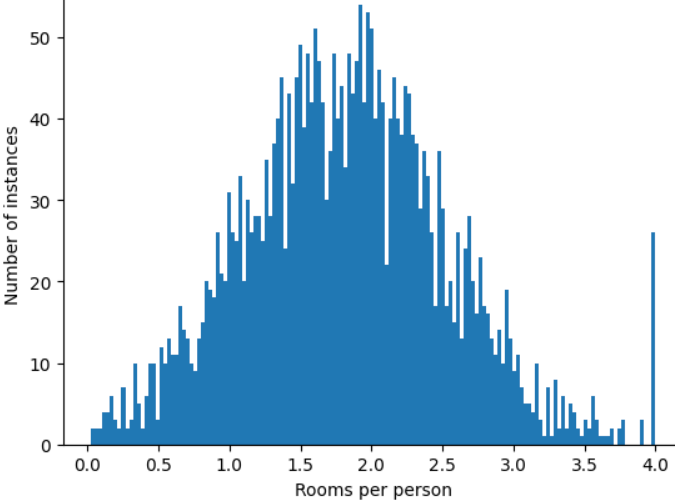
Обрезание значения функции на уровне 4,0 не означает, что ваша модель игнорирует все значения выше 4,0. Скорее, это означает, что все значения, которые были больше 4,0, теперь становятся 4,0. Это объясняет своеобразный холм на 4.0. Несмотря на этот холм, масштабированный набор функций теперь более полезен, чем исходные данные.

Подожди секунду! Можете ли вы действительно свести каждое выбросное значение к некоторому произвольному верхнему порогу? При обучении модели — да.

Вы также можете обрезать значения после применения других форм нормализации. Например, предположим, что вы используете масштабирование по Z-показателю, но некоторые выбросы имеют абсолютные значения, намного превышающие 3. В этом случае вы можете:

• Сократите Z-показатели больше 3, чтобы они стали ровно 3.
• Z-показатель клипа меньше -3 становится ровно -3.

Отсечение предотвращает переиндексацию вашей модели по неважным данным. Однако некоторые выбросы на самом деле важны, поэтому обрезайте значения осторожно.

Краткое описание методов нормализации

Лучший метод нормализации — тот, который хорошо работает на практике, поэтому пробуйте новые идеи, если считаете, что они хорошо сработают в вашем распределении функций.

Метод нормализации	Формула	Когда использовать
Линейное масштабирование	$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$	Когда признак равномерно распределен в фиксированном диапазоне.
Масштабирование Z-оценки	$$ x' = \frac{x - μ}{σ}$$	Когда распределение признаков не содержит крайних выбросов.
Масштабирование журнала	$$ x' = log(x)$$	Когда признак соответствует степенному закону.
Обрезка	Если $x > max$, установите $x' = max$ Если $x < min$, установите $x' = min$	Когда объект содержит экстремальные выбросы.

Упражнение: Проверьте свои знания.

Какой метод наиболее подходит для нормализации признака со следующим распределением?

Масштабирование Z-оценки

Точки данных обычно соответствуют нормальному распределению, поэтому масштабирование Z-показателя приведет их к диапазону от –3 до +3.

Линейное масштабирование

Просмотрите обсуждения методов нормализации на этой странице и повторите попытку.

Масштабирование журнала

Просмотрите обсуждения методов нормализации на этой странице и повторите попытку.

Обрезка

Просмотрите обсуждения методов нормализации на этой странице и повторите попытку.

Предположим, вы разрабатываете модель, которая прогнозирует производительность центра обработки данных на основе температуры, измеренной внутри центра обработки данных. Почти все значения temperature в вашем наборе данных находятся в диапазоне от 15 до 30 (по Цельсию), за следующими исключениями:

• Один или два раза в год, в очень жаркие дни, temperature фиксируется в пределах от 31 до 45.
• Каждая тысячная точка temperature устанавливается на 1000, а не на фактическую температуру.

Какой метод нормализации temperature был бы разумным?

Обрежьте значения выбросов между 31 и 45, но удалите выбросы со значением 1000.

Значения 1000 являются ошибками и должны быть удалены, а не обрезаны.

Значения между 31 и 45 являются допустимыми точками данных. Отсечение этих значений, вероятно, было бы хорошей идеей, если предположить, что набор данных не содержит достаточно примеров в этом диапазоне температур, чтобы обучить модель делать хорошие прогнозы. Однако во время вывода обратите внимание, что усеченная модель будет давать тот же прогноз для температуры 45, что и для температуры 35.

Обрезать все выбросы

Просмотрите обсуждения методов нормализации на этой странице и повторите попытку.

Удалить все выбросы

Просмотрите обсуждения методов нормализации на этой странице и повторите попытку.

Удалите значения выбросов между 31 и 45, но обрежьте выбросы со значением 1000.

Просмотрите обсуждения методов нормализации на этой странице и повторите попытку.

Ключевые термины:

• Обрезка
• NaN-ловушка
• Нормализация
• Масштабирование
• Нормализация Z-показателя