到目前為止,我們在討論公平性指標時誤以為 和測試樣本包含該客層的 個接受評估的子群組。但情況通常並非如此。
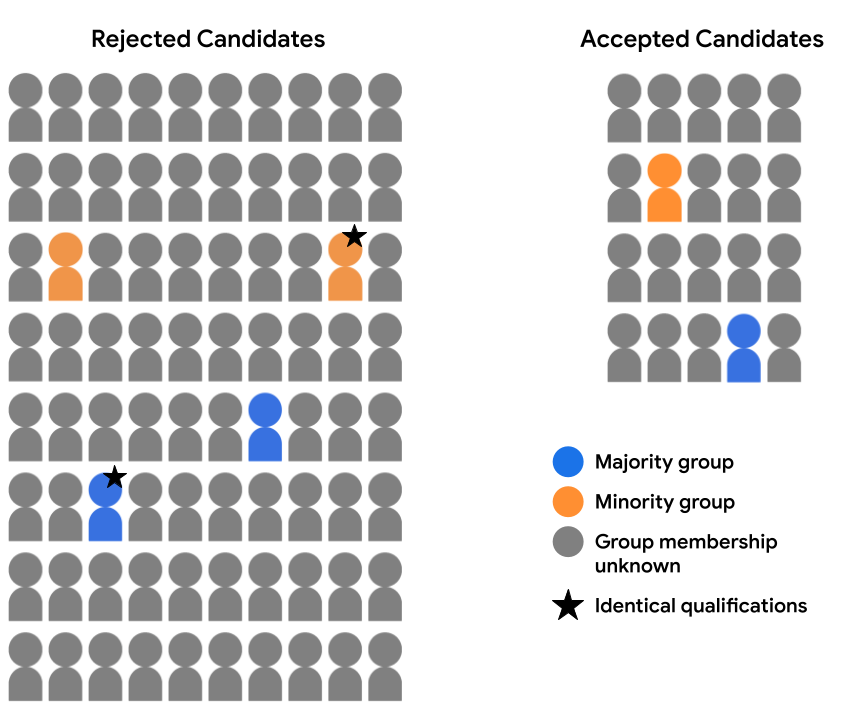
假設我們的招生資料集並未包含完整的客層資料。 而是只記錄少部分客層的成員資格 例如選擇自行識別哪個群體的學生 相關單位。本例中,我們接受的候選名單細分為已接受 遭到拒絕的學生看起來會像這樣:

不能在這裡評估任一客層的模型預測結果 表示商機的對等或平等,因為我們沒有客層資料 94% 的樣本然而,就 6% 的樣本 客層特徵,我們仍可比較個別預測結果的組合 (絕大多數候選人和少數候選人) 以均衡處理
假設我們詳細審查了地圖項目資料 兩位候選人可用 (一對多數候選人和一位未成年人 下方圖片中標上星號),並且認定他們 不論在任何場合,都符合入學資格。如果模型 兩者的預測結果相同 (也就是說,兩者都拒絕 或接受兩種候選人) 表示符合counterfactual 公平性。反事實的公平性是指 除了特定敏感屬性以外,所有層面都相同的例子 也就是客層群組成員) 都應採用相同的模式 預測結果
優點和缺點
先前提過,「反事實查核」的主要益處 可用於評估預測結果的公平性 就無法提供其他指標如果資料集不包含完整的 相關群組屬性的特徵值時, 以便評估公平性 商機。不過,如果這些群組屬性適用於部分群組 不過,我們能找出可比較的相等組合 從不同群體的樣本中,從業人員可以提出反事實的公平性 視為指標,向模型探測預測中潛在偏誤。
此外,因為 機會評估各個群體,能掩蓋影響 並在個別預測結果層級 並進行反事實審查例如,假設 模型接受多數團體的合格候選人,以及未成年人 具有相同比例的群體,但最符合資格的少數候選人是 其他競爭激烈的候選人 是否接受憑證您可以透過反事實的公平性分析 以便加以解決
另一方面,反事實公平性的關鍵缺點在於 讓您全面掌握模型預測結果中的偏誤。識別與 以一連串的例子補救少量不平等的做法可能不足以解釋 解決影響整個子群組的系統性偏誤問題。
如果可行的話,從業人員可以考慮兩種匯總資料 公平性分析 (使用如人口統計對等性或 ) 以及反事實公平性分析, 深入探討需要修復的潛在偏誤問題範圍
練習:隨堂測驗
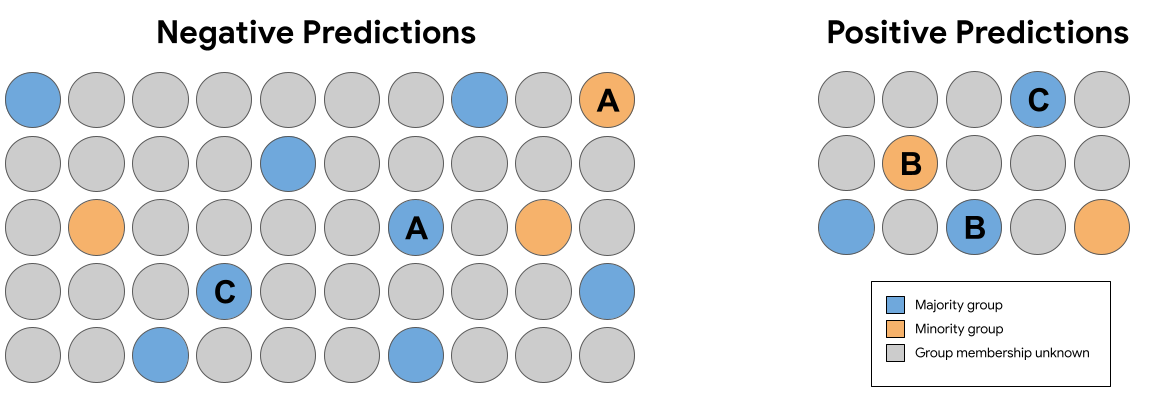
在上方圖 7 的預測結果中, 下列組合完全相同 (不包括群組成員) 樣本是否符合反事實的公平性?
摘要
客層一致、 機會平等 每項模型都提供不同的數學定義 確保模型預測的公平性這裡只列出三個例子 以及量化公平性的方法公平性的一些定義甚至會互相影響 不相容, 換句話說,要同時滿足這兩個條件 預測結果
在這種情況下,該如何選擇「右側」適合自家模型的公平性指標呢?您需要執行的操作 考量使用情境以及主要目標 您想達成的目標例如,是否的目標是達到 (在本例中,客層差異可能是最佳指標),還是 機會平等 (在這裡,機會平等可能 指標)?
如要進一步瞭解機器學習公平性並進一步探索這些問題,請參見 Solon Barocas、Moriz Hardt 和 Arvind Narayanan 的《Fairness and Machine Learning: Limitations and Opportunity》。
